Chi-Quadrat-Verteilungstest

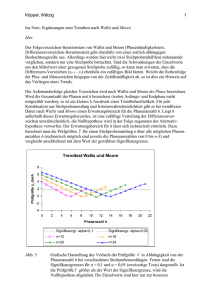
Chi-Quadrat-Verteilungstest
Anwendung:
Test, ob die in der SP beobachtete Verteilung mit
einer theoretischen Verteilung aus der GG
übereinstimmt.
Schritt 1: Hypothesen
H 0 : Zufallsvariable folgt einer best. Verteilung
H A : Zufallsvariable folgt NICHT einer best. Verteilung
Schritt 2: Prüfgröße und Testverteilung
Basis:
k
χ² = ∑
i =1
Quadrierte Abstände zwischen beobachteten
Zellhäufigkeiten der Stichprobe und den theoretischen
Zellhäufigkeiten unter H 0 .
(ni − n ⋅ pi )²
~ χ²(k − 1)
n ⋅ pi
(unter H0 )
wobei:
ni: empirische Zellhäufigkeiten (SP)
pi: Wahrscheinlichkeitsverteilung unter H0
n ⋅ pi: theoretische Zellhäufigkeiten unter H0
k:
Anzahl der Zellen
Schritt 3: Kritischer Bereich
Rechtsseitiger Test
KB: [χ12−α;k −1 ; +∞[
Anmerkung:
Test nur durchführbar, wenn n ⋅ pi ≥ 5 (nur bei relativ großen SP).
Chi-Quadrat-Unabhängigkeitstest
Anwendungsgebiet:
Test, ob zwei NOMINAL skalierte Variablen stochastisch unabh. sind
Schritt 1: Hypothesen
H 0 : Zufallsvariablen sind stochastisch unabhängig.
H A : Zufallsvariablen sind stochastisch abhängig.
Schritt 2: Prüfgröße und Testverteilung
Basis:
Quadrierte Abstände zwischen beobachteten
Zellhäufigkeiten der Stichprobe und den theoretischen
Zellhäufigkeiten unter H 0 (vgl. Chi-QuadratVerteilungstest).
r
s
χ² = ∑∑
i =1 j =1
(nij − n% ij )²
~ χ²[(r − 1) ⋅ (s − 1)]
n% ij
(unter H0 )
wobei:
nij: empirische Zellhäufigkeiten (SP)
n% ij : theoretische Zellhäufigkeiten unter H0 (bei Unabh.)
wobei n% ij =
r:
s:
n i⋅ ⋅ n ⋅ j
n
Anzahl der Spalten
Anzahl der Zeilen
Schritt 3: Kritischer Bereich
Rechtsseitiger Test
KB: [χ12−α;(r− 1)(s
⋅ −1) ; +∞[
Beispiel:
Chi-Quadrat-Verteilungstest
Sie vermuten, dass die neue 2€-Münze nicht fair ist. Sie werfen die
Münze jeweils 5mal. Das Experiment führt zu folgenden Ergebnissen:
Anzahl der Wappen (X)
Empirische HK (ni)
0
32
1
44
2
64
3
24
4
20
5
16
Schritt 1: Hypothesen
H 0 : DieVariable 'Anzahl Wappen'ist binomialverteilt − X ~ B(5;0,5)
H A : DieVariable 'Anzahl Wappen'ist NICHT binomialverteilt
Schritt 2: Prüfgröße und Testverteilung
k
χ² = ∑
i =1
(ni − n ⋅ pi )²
~ χ²(k − 1)
n ⋅ pi
Schritt 3: Kritischer Bereich
2
2
χcrit
= χ12−α;k −1 = χ 0,95;5
= 11,070
KB: [11,070; +∞[
(unter H0 )
Schritt 4: Wert der Prüfgröße
Anzahl der
0
1
2
3
4
5
Wappen (X)
Empirische HK (ni)
32
44
64
24
20
16
unter H0: X~B(5;0,5)
0,0313 0,1563 0,3125 0,3125 0,1563 0,0313
p i = P(X = x i )
6,26 31,26 62,5
62,5
31,26 6,26
n ⋅ pi = 200 ⋅ pi
662,55 137,83 2,25 1482,25 126,79 94,87
(n i − n ⋅ pi )²
(n i − n ⋅p i )²
105,84 4,41 0,04
23,72
4,06 15,15
n ⋅ pi
Test durchführbar, wenn n ⋅ pi ≥ 5 (OK).
k
χ² = ∑
i =1
(ni − n ⋅ pi )²
= 153,22
n ⋅ pi
Schritt 5: Entscheidung
χ² ∈ KB
:
H0 ablehnen
Mit 95%-iger Wahrscheinlichkeit ist die Variable ‚Anzahl der
Wappen’ nicht biomialverteilt (Münze nicht fair).
70
60
50
40
Empirisches n
Theoretisches n
30
20
10
0
0
1
2
3
4
5
Chi-Quadrat-Unabhängigkeitstest
Abschluß (B)
Eignung (A)
geeignet (A1)
ungeeignet(A2)
∑
DiplomSozialökonom
(B1)
n11 = 14
n21 = 16
n.1 = 30
DiplomKaufmann
(B2)
n12 = 10
n22 = 25
n.2 = 35
DiplomVolkswirt
(B3)
∑
n13 = 16
n23 = 19
n.3 = 35
n1. = 40
n2. = 60
n = 100
Testen Sie, ob der Abschluss und die Eignung voneinander abhängen!
Chi-Quadrat-Unabhängigkeitstest
Schritt 1: Hypothesen
H 0 : ‚Abschluss’ und ‚Eignung’ sind stochastisch unabhängig.
H A : ‚Abschluss’ und ‚Eignung’ sind stochastisch abhängig.
Schritt 2: Prüfgröße und Testverteilung
r
s
χ² = ∑∑
i =1 j =1
(nij − n% ij )²
~ χ²[(r − 1) ⋅ (s − 1)]
%n ij
Schritt 3: Kritischer Bereich
Rechtsseitiger Test
Testverteilung:
χ² = χ ²[(r − 1) ⋅ (s − 1)]
= χ²[2 ⋅1]
= χ²[2]
KB:
[χ20,95;2 ; +∞[
[5,991; +∞[
(unter H0 )
Schritt 4: Wert der Prüfgröße
r
s
χ² = ∑∑
i =1 j =1
(nij − n% ij )²
~ χ²[(r − 1) ⋅ (s − 1)]
%n ij
(unter H0 )
n% ij : theoretische Zellhäufigkeiten unter H0 (bei Unabh.)
n% ij =
Abschluß (B)
Eignung (A)
geeignet (A1)
ungeeignet(A2)
∑
χ² =
n i⋅ ⋅ n ⋅ j
n
DiplomSozialökonom
(B1)
n11 = 12
n21 = 18
n.1 = 30
DiplomKaufmann
(B2)
DiplomVolkswirt
(B3)
∑
n12 = 14
n22 = 21
n.2 = 35
n13 = 14
n23 = 21
n.3 = 35
n1. = 40
n2. = 60
n = 100
(14 − 12)² (16 − 18)² (10 − 14)² (25 − 21)² (16 − 14)² (19 − 21)²
+
+
+
+
+
= 2,937
12
18
14
21
14
21
Schritt 5: Entscheidung
χ² ∉ KB
:
H0 annehmen
Mit 95%-iger Wahrscheinlichkeit kann nicht nachgewiesen werden,
dass ‚Abschluss’ und ‚Eignung’ stochastisch abhängig sind.