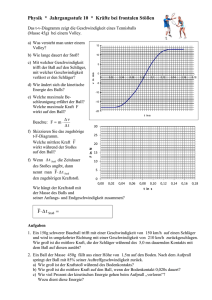
F⋅ t = m⋅ v

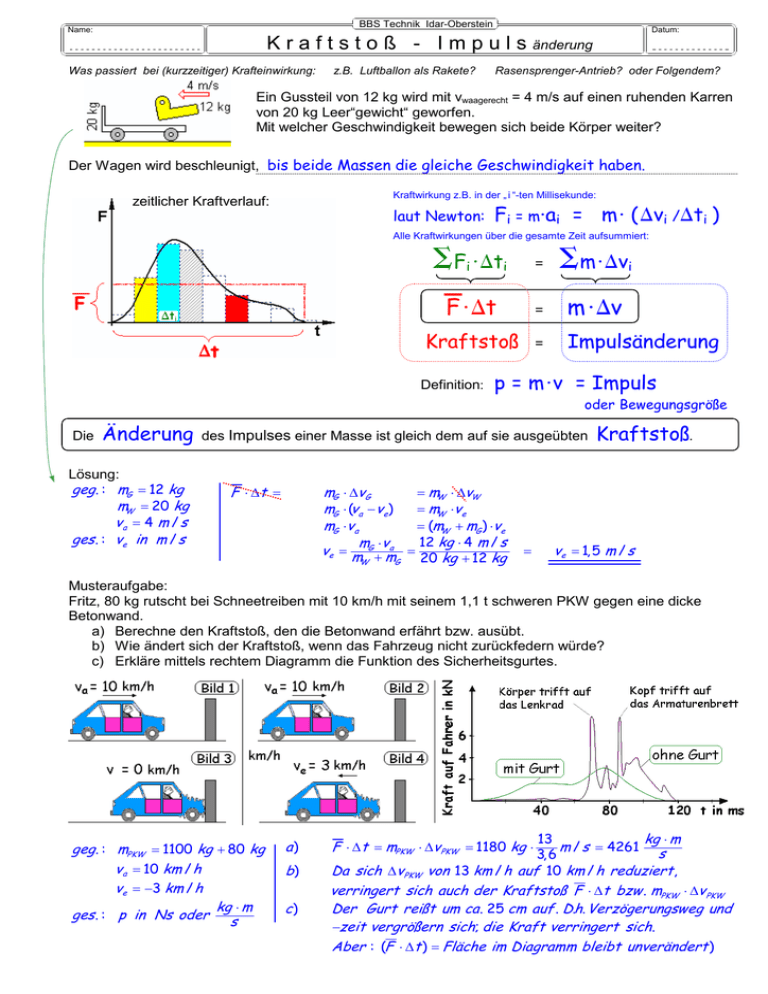
BBS Technik Idar-Oberstein
Name:
Datum:
K r a f t s t o ß - I m p u l s änderung
Was passiert bei (kurzzeitiger) Krafteinwirkung:
z.B. Luftballon als Rakete?
Rasensprenger-Antrieb? oder Folgendem?
Ein Gussteil von 12 kg wird mit vwaagerecht = 4 m/s auf einen ruhenden Karren
von 20 kg Leer“gewicht“ geworfen.
Mit welcher Geschwindigkeit bewegen sich beide Körper weiter?
Der Wagen wird beschleunigt, bis beide Massen die gleiche Geschwindigkeit haben.
Kraftwirkung z.B. in der „ i “-ten Millisekunde:
zeitlicher Kraftverlauf:
laut Newton:
Fi = m⋅ai = m ⋅ ( ∆vi /∆ti )
Alle Kraftwirkungen über die gesamte Zeit aufsummiert:
ΣFi ⋅ ∆ti
=
Σm ⋅ ∆vi
F ⋅ ∆t
=
m ⋅ ∆v
Kraftstoß
=
Impulsänderung
Definition:
p = m ⋅ v = Impuls
oder Bewegungsgröße
Die
Änderung
Lösung:
geg . : mG = 12 kg
mW = 20 kg
va = 4 m / s
ges . : ve in m / s
des Impulses einer Masse ist gleich dem auf sie ausgeübten
F ⋅ ∆t =
mG ⋅ ∆vG
= mW ⋅ ∆vW
= mW ⋅ve
mG ⋅ (va − ve)
= (mW + mG ) ⋅ve
mG ⋅v a
12 kg ⋅ 4 m / s
m ⋅v
ve = m G + ma =
20 kg + 12 kg
W
G
=
Kraftstoß.
ve = 1, 5 m / s
Musteraufgabe:
Fritz, 80 kg rutscht bei Schneetreiben mit 10 km/h mit seinem 1,1 t schweren PKW gegen eine dicke
Betonwand.
a) Berechne den Kraftstoß, den die Betonwand erfährt bzw. ausübt.
b) Wie ändert sich der Kraftstoß, wenn das Fahrzeug nicht zurückfedern würde?
c) Erkläre mittels rechtem Diagramm die Funktion des Sicherheitsgurtes.
geg . : mPKW = 1100 kg + 80 kg
v a = 10 km / h
ve = −3 km / h
kg ⋅ m
ges . : p in Ns oder s
13
kg ⋅ m
m / s = 4261 s
3, 6
von 13 km / h auf 10 km / h reduziert ,
a)
F ⋅ ∆t = mPKW ⋅ ∆v PKW = 1180 kg ⋅
b)
Da sich ∆v PKW
verringert sich auch der Kraftstoß F ⋅ ∆t bzw . mPKW ⋅ ∆v PKW
. . Verzögerungsweg und
Der Gurt reißt um ca . 25 cm auf . Dh
−zeit vergrößern sich; die Kraft verringert sich.
Aber : (F ⋅ ∆t ) = Fläche im Diagramm bleibt unverändert )
c)
BBS Technik Idar-Oberstein
Name:
Datum:
K r a f t s t o ß - I m p u l s änderung
1. a) Erkläre, warum das Newtonsche Grundgesetz auch als Gesetz von der Impulsänderung formuliert werden
kann!
b) Zeige, dass Kraftstoß und Impuls die gleichen Einheiten haben!
a) Newtonsches Grundgesetz:
Wirkt die (gemittelte) Kraft über
eine (Stoß-) Zeit ∆t , so ist
umgestelltes Newtonsches Gesetz :
b) [ F ⋅ ∆t] = [ F ] ⋅[ ∆t] = N ⋅ s =
⋅s
=
kg ⋅ m/s
gleich
[ m ⋅ ∆v] = [ m ] ⋅[ ∆v] = kg ⋅ m/s
2. Ein Hammer von 200 g trifft mit der Geschwindigkeit von 8 m/s einen Nagel, der 5 ms lang in das Holz getrieben
wird.
Wie groß sind ..
1,6 kg ⋅m/s
a) die Impulsänderung des Hammers
b) der Kraftstoß auf den Hammer (und auf den Nagel)
1,6 Ns
c) die (gemittelte) Kraft auf den Nagel?
320 N
geg . : m = 0,2 kg
v = ∆v = 8 m / s
∆t = 5 ms = 0, 005 s
kg ⋅ m
ges . : ∆p in Ns oder s
F in N
3.
Ein Satellit mit der Masse von 500 kg bewegt sich mit einer Geschwindigkeit von 10000 m/s. Diese wird durch eine 10 s
langes Einschalten eines Raketentriebwerkes mit der Schubkraft von 200 N erhöht.
Wie groß sind ...
a) der Kraftstoß,
2000 Ns
2
b) die Beschleunigung,
0,4 m/s
c) die Impulsänderung,
2000 kgm/s
d) die Endgeschwindigkeit?
10004 m/s
geg . : m = 500 kg
v = 10 000 m / s
∆t = 10 s
F = 200 N
ges . : F ⋅ ∆t in Ns
a in m2
s
∆p in kg m
s
m
ve s
4.
F ⋅ ∆t = m ⋅ ∆v
m
m ⋅ ∆v = 0,2 kg ⋅ 8 m
s = 1, 6 kg ⋅ s
Kraftstoß = lmpulsänderung = 1, 6 kg ⋅ m
s
m
F ⋅ ∆t = 1, 6 kg ⋅ s
⇒
1, 6 kg ⋅ m
s = 320 kg ⋅ m = 320 N
⇒F =
0, 005 s
s2
F ⋅ ∆t = 200 N ⋅ 10 s = 2 000 Ns
F
200 kg ⋅ m / s 2
F = m ⋅a ⇒ a = m =
= 0, 4 m2
kg
s
m ⋅ ∆v = F ⋅ ∆t = 2 000 kg ⋅ m
s
m
F ⋅ ∆t 2 000 kg ⋅ s
∆v =
=
=4 m
m
s
500 kg
⇒ ve = v a + ∆v = 10 004 m
s
Mit einem Schlosserhammer wird
a) auf eine gehärtet Ambossplatte und unter sonst gleichen Bedingungen
b) auf einen Hartholzklotz geschlagen.
Begründe, warum die erzielte max. Kraft unterschiedlich groß ist!
Der Kraftstoß (
) ist in beiden Fällen gleich, da m ⋅ ∆v gleich bleibt.
Da die Aufschlagzeit ∆t bei der Ambossplatte sehr, sehr klein ist, muss
(ve Hammer = 0)
sehr groß sein.
BBS Technik Idar-Oberstein
Name:
Datum:
K r a f t s t o ß - I m p u l s änderung
5.
Die 4 Strahltriebwerke eines Düsenflugzeuges von 150 t sollen (beim Start) eine Schubkraft von 210 kN erreichen. Die
Verbrennungsgase haben dabei eine Ausströmgeschwindigkeit von 2000 m/s. (geschätzt)
105 kg
a) Wie viel kg Verbrennungsgas strömen in 1 Sekunde durch die Triebwerke?
b) Wann hat das Flugzeug seine Startgeschwindigkeit von 70 m/s erreicht?
50 s
geg . : mFl = 150 000 kg
F = 210 000 N
vGas = ∆v = 2 000 m / s
vFl = 70 m / s
ges . : mGas in kg
bzw . mGas in kg / s
∆t = in s
a)
Für ∆t =1 Sekunde :
F Gas ⋅ ∆t = mGas ⋅ ∆vGas
m
F Gas ⋅ ∆t 210 000 kg s 2 ⋅ 1 s
=
=
= 105 kg
∆vGas
2000 m / s
mGas
b)
Während ∆t Sekunden :
F ⋅ ∆t = mGas ⋅ ∆vGas = mFlugzeug ⋅ ∆vFlugzeug
∆t =
6.
bzw . m =105 kg / s
mFlugzeug ⋅ ∆vFlugzeug 150 000 kg ⋅ 70 m / s
=
= 50 s
F
210 000 kg m2
s
2
Ein Rasensprenger mit einem Düsenquerschnitt von 5 mm „verbraucht“ (pro Düse) 3
Liter Wasser in der Minute.
Berechne die rückstoßende Kraft pro Düse!
0,5 N
geg . : ∆t = 60 s
m = 3 kg
ges . : F in N
v = ts
3000 cm 3
s = Volumen =
= 60 000 cm
Fläche
0, 05 cm 2
60 000 cm
= 10 m
s
60 s
F ⋅ ∆t = m ⋅ ∆v
v =
3 kg ⋅ 10 m
s = 0, 5 kg ⋅ m = 0,5 N
F = m∆⋅ t∆v =
60 s
s2
7.
Skizziert ist die Schaufel einer Peltonturbine, die als Antrieb bei hohen Wassergeschwindigkeiten
(Fallhöhe > 100 m) verwendet wird.
o
a) Begründe, warum man durch die Schaufelform den Wasserstrahl fasst um 180 umlenkt!
b) Durch die Drehung der Turbine hat die Schaufel ebenfalls eine Geschwindigkeit.
Beschreibe qualitativ die Abhängigkeit des Turbinendrehmoments (~Kraft auf die Schaufel)
von der Turbinendrehzahl! (Die Wassergeschwindigkeit sei konstant.)
c) Wo liegt der optimale Wirkungsgrad (ca. 88%) der Turbine?
a) Der mit v ankommende Wasserstrahl wird von der Schaufel nicht nur auf v = 0 verzögert, sondern
in die umgekehrte Richtung beschleunigt.
│∆v│ ist deshalb nicht │v│, sondern fast 2 ⋅ │v│
Die Impulsänderung (und damit auch der Kraftstoß auf die Schaufel) ist deshalb ca. doppelt so groß
wie beim seitlichen Abspritzen des Wassers.
b) Beim Stillstand der Schaufel ist │∆v│
und damit der Kraftstoß am größten.
Dreht die Schaufel so schnell wie die
Wassergeschwindigkeit, so ist ∆v = 0
und F⋅∆t = 0
c) Der optimale Wirkungsgrad muss
zwischen f = 0 und max. Drehfrequenz
liegen.
F
(Turbinen-Drehmoment ist proprotional zur Kraft)
f Drehfrequenz
η=0
denn ∆p = 0,
da v = 0
η = max
η=0
denn ∆p = 0,
da ∆v = 0 und F = 0
genauer: Er liegt genau in der Hälfte, denn:
bei vSchaufel = ½ vWasser wird wird der Wasserstrahl so umgelenkt, dass er nach Verlassen der
Schaufel keine Geschwindigkeit und keine kinetische Energie mehr hat.
BBS Technik Idar-Oberstein
Name:
Datum:
K r a f t s t o ß - I m p u l s änderung
8.
Skizziert ist eine (ungeschickte) Anordnung eines Hydraulikschlauches.
a) Weshalb treten am Schlauch Kräfte auf, wenn über ein Ventil Öl zum Hydraulikzylinder fließt
(auch wenn im Schlauch kaum Druckänderungen entstehen)?
b) In welche Richtung wirkt die entstehende Kraft?
c) Was ändert sich, wenn der Ölstrom beim Zurückfließen die doppelte Geschwindigkeit hat?
a)
+
b)
Impulsänderung im Schlauch = Kraftstoß
m ⋅ ∆v = F ⋅ ∆t
Fabbremsen
m ⋅ (ve - va) = F ⋅ ∆t
jew. für x- und y-Richtung:
Fbeschleunigen
c) Bei doppelter Strömungsgeschwindigkeit verdoppelt sich auch die Masse, die pro ∆t durch den
Schlauch fließt.
2⋅m ⋅ 2⋅∆v 4-fache Impulsänderung die Kraft ist 4-mal so groß.
Ihre Richtung jedoch bleibt die gleiche. (Was oben die Abbremskraft war, ist jetzt die
Beschleunigungskraft und umgekehrt.)