Bewegung: rotatorischen Die gleichförmige, geradlinige Bewegung

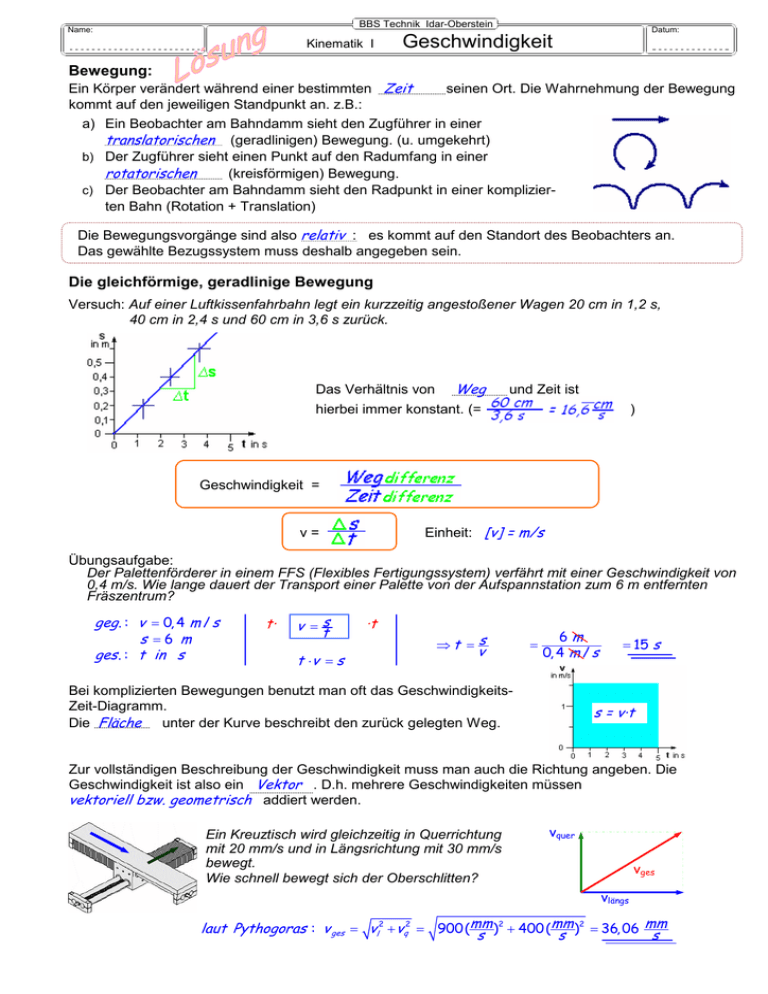
BBS Technik Idar-Oberstein
Name:
Kinematik I
Datum:
Geschwindigkeit
Bewegung:
Ein Körper verändert während einer bestimmten Zeit
seinen Ort. Die Wahrnehmung der Bewegung
kommt auf den jeweiligen Standpunkt an. z.B.:
a) Ein Beobachter am Bahndamm sieht den Zugführer in einer
translatorischen (geradlinigen) Bewegung. (u. umgekehrt)
b) Der Zugführer sieht einen Punkt auf den Radumfang in einer
rotatorischen
(kreisförmigen) Bewegung.
c) Der Beobachter am Bahndamm sieht den Radpunkt in einer komplizierten Bahn (Rotation + Translation)
Die Bewegungsvorgänge sind also relativ : es kommt auf den Standort des Beobachters an.
Das gewählte Bezugssystem muss deshalb angegeben sein.
Die gleichförmige, geradlinige Bewegung
Versuch: Auf einer Luftkissenfahrbahn legt ein kurzzeitig angestoßener Wagen 20 cm in 1,2 s,
40 cm in 2,4 s und 60 cm in 3,6 s zurück.
Das Verhältnis von
Weg
und Zeit ist
hierbei immer konstant. (=
)
Geschwindigkeit =
Einheit: [v] = m/s
v=
Übungsaufgabe:
Der Palettenförderer in einem FFS (Flexibles Fertigungssystem) verfährt mit einer Geschwindigkeit von
0,4 m/s. Wie lange dauert der Transport einer Palette von der Aufspannstation zum 6 m entfernten
Fräszentrum?
geg . : v = 0, 4 m / s
s =6 m
ges . : t in s
t⋅
v = ts
t ⋅v = s
⋅t
⇒t = s
v
=
6m
0, 4 m / s
Bei komplizierten Bewegungen benutzt man oft das GeschwindigkeitsZeit-Diagramm.
Die Fläche unter der Kurve beschreibt den zurück gelegten Weg.
= 15 s
s = v⋅t
Zur vollständigen Beschreibung der Geschwindigkeit muss man auch die Richtung angeben. Die
Geschwindigkeit ist also ein Vektor . D.h. mehrere Geschwindigkeiten müssen
vektoriell bzw. geometrisch addiert werden.
Ein Kreuztisch wird gleichzeitig in Querrichtung
mit 20 mm/s und in Längsrichtung mit 30 mm/s
bewegt.
Wie schnell bewegt sich der Oberschlitten?
vquer
vges
vlängs
2
mm 2
mm
laut Pythogoras : v ges = vl2 + vq2 = 900(mm
s ) + 400 ( s ) = 36, 06 s
BBS Technik Idar-Oberstein
Name:
Kinematik I
Geschwindigkeit
Datum:
Aufgaben L
1. Ein Motorrad legt alle 4 s 100 m zurück.
a) Welche Geschwindigkeit müsste auf seinem Tachometer abzulesen sein?
b) Welche Umrechnungszahl von m/s auf km/h sollte man sich merken? (kurz herleiten)
geg . : ∆s = 100 m
∆t = 4 s
ges . : v in km / h
s = 100 m = 25 m
v =∆
∆t
s
4s
km /1000
km
3600 km
v = 25 m
s = 25 h /3600 = 25 ⋅ 1000 h = 90 h
2.
Umrechnungszahl: 3,6
Bei der Ultraschallprüfung eines Werkstückes aus Stahlguss wird am Oszillator
eine Reflexionszeit von 3,2 µs festgestellt. (Schallgeschwindigkeit von Stahl
≅ 4900 m/s)
In welcher Tiefe befindet sich der Lunker (=Fehlstelle im Guss)?
geg . : t = 3,2 ⋅ 10 −6 s
v = 4900 m / s
ges . : s / 2 in m
t⋅
v = ts ⋅ t
−6
s = v ⋅t = 4900 m
s ⋅ 3,2 ⋅ 10 s
s = 1,57 ⋅ 10 −2 m = 15, 7 mm
⇒ Tiefe = s = 7,84 mm
2
3. Eine CNC-Fräsmaschine fräst eine Werkstückkante von 360 mm Länge. Die Vorschubgeschwindigkeit wurde auf
150 mm/min programmiert (F150).
Wie lange benötigt die Maschine, um die Kante zu fräsen?
geg . : s = 360 mm
v = 150 mm / min
ges . : t in s
4.
t⋅
v = ts
⋅t
v ⋅t = s ⇒ t = s =
⇒
v
v
v
360 mm min
t =
= 2, 4 min = 144 s
150 mm
a) Wie ist die Geschwindigkeit definiert?
b) Wieso ist die Geschwindigkeit ein Vektor?
a) Die Geschwindigkeit ist der Quotient aus Wegänderung durch die Zeitänderung.
Die Einheit ist m/s.
b) ... weil sie zusätzlich noch eine Richtung hat. 2. Geschwindigkeiten addieren sich vektoriell.
5. Ein Mann rudert mit 3,6 km/h senkrecht zu einem Fluss mit einer Wassergeschwindigkeit von 1 m/s und der Breite
von 100 m.
=1 m/s
a) Wie schnell und in welche Richtung bewegt sich?
b) Wann erreicht der Kahn das andere Ufer?
c) Hätte der Ruderer ein Chance, auf Höhe des Beobachters (also senkrecht
zum Flusslauf) das Gewässer zu überqueren? (Skizzen)
vFluss
b)
vres = 1,41 m/s
s
v
in Ruderrichtung = 100 m
in Ruderrichtung = 1 m/s
c) Nein, denn
vres = 0.
t = s/v = 100 s
vRuderer ist nicht größer als vFluss .
6. Ein Hallenkran hebt ein 1,4 t schweres Maschinenteile mit einer Hubgeschwindigkeit von 0,1 m/s
hoch. Gleichzeitig verfährt der Kran mit 0,4 m/s in Längsrichtung der Halle und die „Laufkatze“ des
Krans mit 0,4 m/s quer zur Halle.
Wie groß ist die Gesamtgeschwindigkeit des transportierten Werkstücks?
vres 1 ist laut Pythagoras
vres
(0,4 m/s)2 + (0,4 m/s)2 = 0,566 m/s
(projiziert) auf
die Ebene
vres 2 ist laut Pythagoras
(0,566 m/s)2 + (0,1 m/s)2 = 0,574 m/s
im Raum
BBS Technik Idar-Oberstein
Name:
Kinematik I
Geschwindigkeit
Datum:
Aufgaben L
7. Nach einer Testfahrt eines neuen Baustellenfahrzeuges wird rechts
stehender „Fahrtenschreiber“ ausgewertet.
Ermittle ...
a) die maximale Geschwindigkeit ~ 3,4 km/s
b) die minimale Geschwindigkeit ~ -1,6 km/s
~ 1,8 km/s
c) die Durchschnittsgeschwindigkeit.
d) Welche Vorteile hat dem gegenüber ein v-t-Diagramm?
3,4 h
d) ... man sieht zu jedem Zeitpunkt die jeweilige Geschwindigkeit und man erkennt an der
Fläche (unterhalb der Kurve) den zurückgelegten Weg.