Rechtecke und Quadrat
Werbung
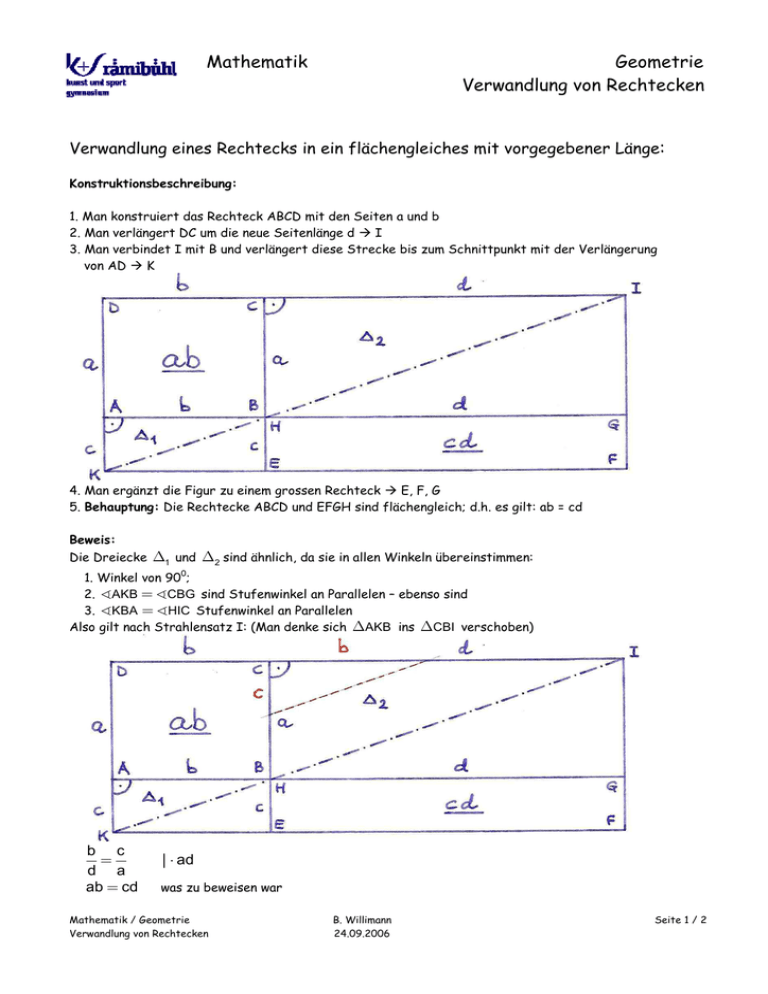
Mathematik Geometrie Verwandlung von Rechtecken Verwandlung eines Rechtecks in ein flächengleiches mit vorgegebener Länge: Konstruktionsbeschreibung: 1. Man konstruiert das Rechteck ABCD mit den Seiten a und b 2. Man verlängert DC um die neue Seitenlänge d I 3. Man verbindet I mit B und verlängert diese Strecke bis zum Schnittpunkt mit der Verlängerung von AD K 4. Man ergänzt die Figur zu einem grossen Rechteck E, F, G 5. Behauptung: Die Rechtecke ABCD und EFGH sind flächengleich; d.h. es gilt: ab = cd Beweis: Die Dreiecke ∆1 und ∆2 sind ähnlich, da sie in allen Winkeln übereinstimmen: 1. Winkel von 900; 2. ∢AKB = ∢CBG sind Stufenwinkel an Parallelen – ebenso sind 3. ∢KBA = ∢HIC Stufenwinkel an Parallelen Also gilt nach Strahlensatz I: (Man denke sich ∆AKB ins ∆CBI verschoben) b c = d a ab = cd │ ⋅ ad was zu beweisen war Mathematik / Geometrie Verwandlung von Rechtecken B. Willimann 24.09.2006 Seite 1 / 2 Mathematik Geometrie Verwandlung von Rechtecken Verwandlung eines Rechtecks in ein flächengleiches Quadrat: Konstruktionsbeschreibung - gemäss Höhensatz des Euklid: 1. Man konstruiert das Rechteck ABCD mit den Seiten p und q; diese werden als die Höhenabschnitte eines rechtwinkligen Dreiecks aufgefasst 2. Man verlängert AB nach rechts und trägt p = BC darauf ab E 3. Man halbiert AE = c M 4. Man konstruiert den Thaleskreis über AE 5. Man schneidet die Verlängerung von CB mit dem Thaleskreis F 6. BF ist die Höhe im Dreieck AEF 7. Nach dem Höhensatz des Euklid gilt nun: pq = h2 Somit ist das Rechteck ABCD in das flächengleiche Quadrat HBFG verwandelt. Mathematik / Geometrie Verwandlung von Rechtecken B. Willimann 24.09.2006 Seite 2 / 2











