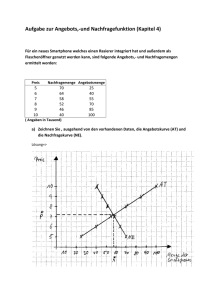
Variante A - FH Bingen
Werbung

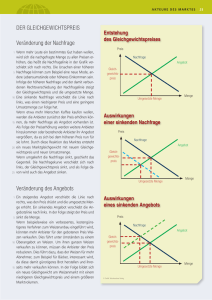
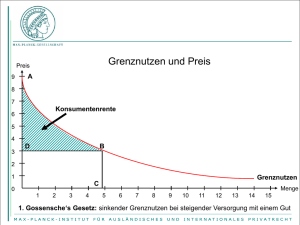
Wirtschaftstheoretische Grundlagen Ressourcenökonomie Mikroökonomie Ziel: effiziente Lösung von Knappheitsproblemen Mögliche Lösung von Knappheitsprobleme Gewalt Regeln, Anordnung • Autoritär – Wohlmeinende – Missbräuchlich • Demokratie – „Kluge“, informierte Wähler – „Dumme“, uninformierte Wähler – Instrumentalisierung der Wähler Markt • Vollkommen: erstbeste Lösungen • Unvollkommen: mäßige bis unerwünschte Lösungen Ökonomische Kernfragen Positive Analyse: Wie werden in einer Volkswirtschaft Entscheidungen zur Verwendung knapper Ressourcen getroffen? Normative Analyse • Wie müssen die Rahmenbedingungen aussehen, damit ein effiziente Verwendung knapper Ressourcen gewährleistet ist? Problem: Was ist gesellschaftlich optimal? Gesellschaftliche Optimalität – aus ökonomischer Sicht Das ökonomische Kernproblem: Maximiere den gesellschaftliche Nutzen bei • gegebener Nutzen- und • Produktionsfunktion sowie bei • gegebenem Faktorbestand • Ergebnis des Gedankenmodells (Tafelbild): • Grenznutzen = Preis = Grenzkosten • Hypothese des Polypols Grenznutzen abhängige Variable Grenznutzenfunktion = Nachfragefunktion Preis unabhängige Variable Menge Nachfrage Grenznutzen abhängige Variable Konsumentenrente Preis Ausgaben unabhängige Variable Menge Nachfrage Grenznutzen abhängige Variable Konsumentenrente 1 Konsumentenrente 0 Preis 1 Preis 0 unabhängige Variable Menge 1 Menge 0 Nachfrage Grenznutzen abhängige Variable Änderung der Konsumentenrente Hier: Verlust an Konsumentenrente Preis 1 Preis 0 unabhängige Variable Menge 1 Menge 0 Nachfrage Grenzkosten abhängige Variable Grenzkostenfunktion = Angebotsfunktion im Polypol Annahme: Mengenanpasser! Preis unabhängige Variable Menge Angebot Grenzkosten abhängige Variable Grenzkostenfunktion = Angebotsfunktion im Polypol Produzentenrente = Umsatz - Kosten Preis Kosten unabhängige Variable Menge Angebot Grenzkosten abhängige Variable Grenzkostenfunktion = Angebotsfunktion im Polypol Produzentenrente Preis unabhängige Variable Menge Angebot Grenzkosten abhängige Variable Grenzkostenfunktion = Angebotsfunktion im Polypol Preis 1 Preis 0 Produzentenrente 1 Produzentenrente 0 unabhängige Variable Menge 0 Menge 1 Angebot Grenzkosten abhängige Variable Änderung der Produzentenrente Hier: Gewinn an Produzentenrente Preis 1 Grenzkostenfunktion = Angebotsfunktion im Polypol Preis 0 unabhängige Variable Menge 0 Menge 1 Angebot Wohlfahftsänderung Änderung der Konsumentenrente Änderung der Produzentenrente Grenzkosten Grenznutzen Nachfrage Angebot Das Aggregationsproblem U1 U2 P P x P x x Das Aggregationsproblem U1 U2 P P P A x x x Das Aggregationsproblem Hier muss Präferenzskala nur ordinal angegeben werden U1 Nachfragefunktion ist kardinal skaliert! U2 P P P H1 N H2 P P A x x x x x Das Aggregationsproblem U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Die „geheimnisvolle Kraft“ des Marktes U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Die „geheimnisvolle Kraft“ des Marktes U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Die „geheimnisvolle Kraft“ des Marktes U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Die „geheimnisvolle Kraft“ des Marktes U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Wohlfahrtsmaximum Gut ist über den Markt handelbar Monetarisierbarkeit der Werte Konkurrierender Konsum (Ausschlussprinzip) Eigentumsrecht kostengünstig durchsetzbar Wettbewerb Prinzip der Konsumentensouveränität Unternehmen sind Mengenanpasser Grenznutzen = Preis = Grenzkosten Folge: Abweichen vom Gleichgewichtspreis führt zu Wohlfahrtsverlusten Marktversagen Marktkonzentration Oligopole Monopole Unvollständige Information Informationsasymmetrie The Market of Lemmons - Akerlof Negative externe Effekte Unternehmen 2 produziert Ruß Haushalt 2 leidet darunter Gibt es hierfür eine umweltökonomische Lösung? Produktionseinschränkung wegen Rußemission U1 U2 P Markt P P H1 N H2 P P Gleichgewichtspreis A x x x Gleichgewichtsmenge x x Produktionseinschränkung wegen Rußemission Markt Gleichgewichtspreis P N A Annahme: Rußemission ist proportional zur Produktion des Gutes X! x Gleichgewichtsmenge Produktionseinschränkung wegen Rußemission Markt Gleichgewichtspreis P N A x Gleichgewichtsmenge Produktionseinschränkung wegen Rußemission Markt Gleichgewichtspreis P N A x Gleichgewichtsmenge Produktionseinschränkung wegen Rußemission Gleichgewichtspreis Grenzvermeidungskosten Markt P N A Grenzvermeidungskostenkurve x x Gleichgewichtsmenge Produktionseinschränkung wegen Rußemission Grenzvermeidungskosten der Gesellschaft Achtung: Landwirte! Grenzvermeidungskostenkurve = Grenzwohlfahrtsverlust einer Kontingentierung! Grenzschaden der Geschädigten: Grenzschadenskurve Annahme: die Geschädigten können ihren Schaden monetär bewerten! Grenzvermeidungskostenkurve x Zuweisung des Eigentumsrechts Variante A: Unternehmen kann kostenfrei emitieren Laissez faire Regel Unternehmen ist „Eigentümer“ des Emissionsrechtes Varianten B: Geschädigter kann Entschädigung durchsetzen Verursacherregel Geschädigter ist „Eigentümer“ des Emissionsrechtes Zuordnung des Eigentumsrechts (Coase Theorem) kein moralisches Problem kein Verteilungsproblem nur abhängig von der kostengünstigsten Durchsetzbarkeit Variante A: Unternehmen ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschadenskurve Nutzen der Geschädigten durch Mengenreduktion = Maximale Kompensationszahlung an Unternehmen Grenzvermeidungskostenkurve x Variante A: Unternehmen ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Kosten der Konsumenten und Produzenten durch Produktionseinschränkung Variante A: Unternehmen ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Kosten der Konsumenten und Produzenten durch Produktionseinschränkung Variante A: Unternehmen ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Nutzen der Gesellschaft = Maximaler Gewinn der Unternehmen bei dieser Produktionsreduktion Grenzvermeidungskostenkurve x Variante A: Unternehmen ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Maximaler Nutzen der Gesellschaft = Maximal möglicher Gewinn der Unternehmen und Konsumenten Grenzvermeidungskostenkurve x Variante B: Geschädigter ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Nutzen von Produzenten und Konsumenten durch ProduktionsAusdehnung = Maximale Entschädigungsforderung der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Variante B: Geschädigter ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Kosten der Geschädigten durch Produktionsausdehnung Variante B: Geschädigter ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Kosten der Geschädigten durch Produktionsausdehnung Variante B: Geschädigter ist Eigentümer des Emissionsrechtes Grenzvermeidungskosten der Gesellschaft Grenzschaden der Geschädigten Maximaler Nutzen der Gesellschaft = Maximal möglicher Gewinn der Geschädigten Grenzschadenskurve Grenzvermeidungskostenkurve x Allokation der Eigentumsrechte hat keinen Einfluss auf Ergebnis! Variante A: Unternehmer ist Eigentümer – Laissez faire Regel Varianter B: Geschädigte ist Eigentümer Verursacherregel Ergebnis Negative externe Umwelteffekte lassen sich internalisieren Marktwirtschaftliche Lösung ist an Voraussetzungen gebunden Eigentumsrechte zuweisen Schaden und Nutzen korrekt bewerten Trittbrettfahrereffekte vermeiden Gültigkeit des Coase Theorems?