Aufgaben zu: Interferenz beim Doppelspalt Hausaufgaben zu

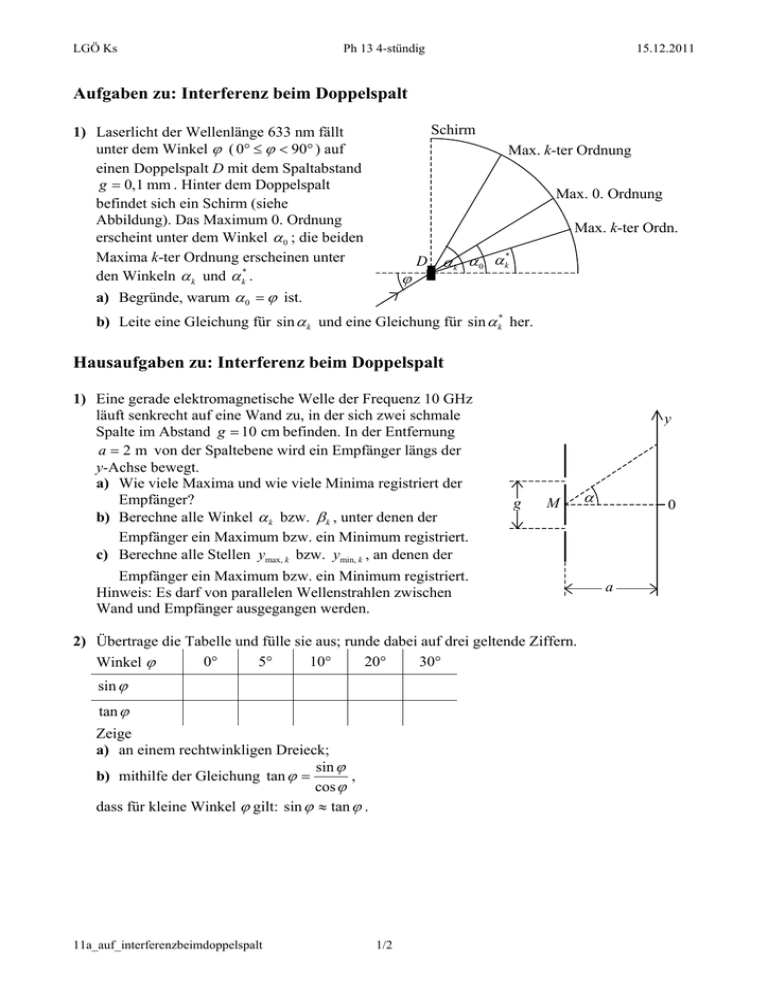
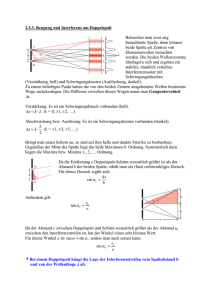
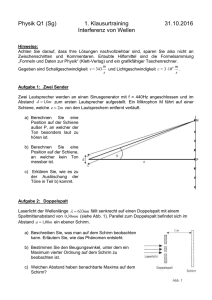
LGÖ Ks
Ph 13 4-stündig
15.12.2011
Aufgaben zu: Interferenz beim Doppelspalt
Schirm
1) Laserlicht der Wellenlänge 633 nm fällt
unter dem Winkel ϕ ( 0° ≤ ϕ < 90° ) auf
einen Doppelspalt D mit dem Spaltabstand
g = 0,1 mm . Hinter dem Doppelspalt
befindet sich ein Schirm (siehe
Abbildung). Das Maximum 0. Ordnung
erscheint unter dem Winkel α 0 ; die beiden
Maxima k-ter Ordnung erscheinen unter
den Winkeln α k und α k* .
a) Begründe, warum α 0 = ϕ ist.
Max. k-ter Ordnung
Max. 0. Ordnung
Max. k-ter Ordn.
ϕ
*
D αk α0 αk
b) Leite eine Gleichung für sin α k und eine Gleichung für sin α k* her.
Hausaufgaben zu: Interferenz beim Doppelspalt
1) Eine gerade elektromagnetische Welle der Frequenz 10 GHz
läuft senkrecht auf eine Wand zu, in der sich zwei schmale
Spalte im Abstand g = 10 cm befinden. In der Entfernung
a = 2 m von der Spaltebene wird ein Empfänger längs der
y-Achse bewegt.
a) Wie viele Maxima und wie viele Minima registriert der
Empfänger?
b) Berechne alle Winkel α k bzw. β k , unter denen der
Empfänger ein Maximum bzw. ein Minimum registriert.
c) Berechne alle Stellen ymax, k bzw. ymin, k , an denen der
y
g
M
Empfänger ein Maximum bzw. ein Minimum registriert.
Hinweis: Es darf von parallelen Wellenstrahlen zwischen
Wand und Empfänger ausgegangen werden.
2) Übertrage die Tabelle und fülle sie aus; runde dabei auf drei geltende Ziffern.
0°
5°
10°
20°
30°
Winkel ϕ
sin ϕ
tan ϕ
Zeige
a) an einem rechtwinkligen Dreieck;
sin ϕ
b) mithilfe der Gleichung tan ϕ =
,
cos ϕ
dass für kleine Winkel ϕ gilt: sin ϕ ≈ tan ϕ .
11a_auf_interferenzbeimdoppelspalt
1/2
α
0
a
LGÖ Ks
Ph 13 4-stündig
15.12.2011
3) Rotes Licht der Wellenlänge λrot = 633 nm trifft senkrecht auf einen Doppelspalt. Im Abstand
von 1,9 m steht parallel zur Spaltebene ein 16 cm breiter, ebener Schirm. Das Maximum nullter
Ordnung liegt in der Schirmmitte.
Hinweis: Verwende die Näherung für kleine Winkel, falls möglich.
a) Die beiden Maxima erster Ordnung haben den Abstand 4,8 cm. Berechne den Spaltabstand.
b) Welches ist das Maximum höchster Ordnung, das auf dem Schirm beobachtet werden kann?
Wie viele Maxima sind auf dem Schirm zu sehen?
Welchen Abstand haben diese Maxima von der Schirmmitte?
c) Nun fällt zusätzlich blaues Licht der Wellenlänge λblau = 436 nm auf den Doppelspalt.
Wie viele blaue Maxima sind auf dem Schirm zu sehen?
Welchen Abstand haben diese Maxima von der Schirmmitte?
Zeichne für eine Hälfte des Schirms die roten und die blauen Maxima.
4) Zwei Wellenlängen λ1 und λ2 ( λ2 > λ1 ) werden durch einen Doppelspalt in k-ter Ordnung
gerade noch getrennt, wenn das Maximum k-ter Ordnung von λ2 mit dem Minimum ( k + 1) -ter
Ordnung von λ1 zusammenfällt.
a) Welche Wellenlänge λ2 wird in der 4. Ordnung gerade noch von λ1 = 560 nm getrennt?
b) Bis zu welcher Ordnung wird die Wellenlänge λ1 = 580 nm gerade noch von der Wellenlänge λ2 = 630 nm getrennt?
5) Laserlicht der Wellenlänge 633 nm fällt
unter dem Winkel ϕ ( 0° ≤ ϕ < 90° ) auf
einen Doppelspalt D mit dem Spaltabstand
g = 0,1 mm . Hinter dem Doppelspalt
befindet sich ein Schirm (siehe
Abbildung). Die beiden Maxima k-ter
Ordnung erscheinen unter den Winkeln α k
Schirm
Max. k-ter Ordnung
Max. k-ter Ordn.
und α k* .
*
D αk α0 αk
Für welche Winkel ϕ können beide
ϕ
Maxima 5. Ordnung auf dem Schirm
beobachtet werden?
Hinweis: Verwende die Ergebnisse von Aufgabe 1).
6) Grünes Laserlicht der Wellenlänge 546 nm trifft senkrecht auf einen Doppelspalt mit dem Spaltabstand 0,6 mm. Im Abstand 3,5 m steht parallel zur Spaltebene ein ebener Schirm. Der Ort des
Maximums nullter Ordnung wird markiert.
a) Berechne den Abstand der beiden Maxima 5. Ordnung.
b) Der Raum zwischen der Spaltebene und dem Schirm ist mit Wasser ( n = 1,33 ) gefüllt.
Wie groß ist jetzt der Abstand der beiden Maxima 5. Ordnung?
c) Das Wasser zwischen der Spaltebene und dem Schirm wird entfernt.
Vor den unteren Spalt (die Spalte verlaufen waagrecht) wird ein 7 µ m dickes Glasplättchen
( n = 1, 6 ) gehalten.
Bestimme die Lage des Maximums 0. Ordnung auf dem Schirm.
Abituraufgaben (nach Stark-Heft 2011)
Abitur 2006 Aufgabe III a) und Abitur 2007 Aufgabe III c)
11a_auf_interferenzbeimdoppelspalt
2/2