Klassische Mechanik

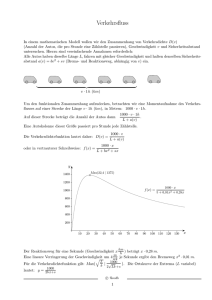
Klassische Mechanik - Ferienkurs
Sommersemester 2011, Prof. Metzler
1
Inhaltsverzeichnis
1 Keplergesetze
3
2 Zweikörperproblem
3
3 Zentralkräfte
4
4 Bewegungen im konservativen Zentralkraftfeld
5
5 Lenzscher Vektor
7
6 Effektives Potential
8
7 Corioliskraft, Zentrifugalkraft
8
2
1
Keplergesetze
1. Die Plantenbahnen sind Ellipsen, mit der Sonne in einem der Brennpunkte.
2. Der Ortsvektor (Verbindungsline Sonne - Planet) überstreicht in gleichen Zeiten gleiche Flächen.
3.
TP2 lanet1
TP2 lanet2
=
a3P lanet1
a3P lanet2
wobei T die Umlaufszeit und a die große Bahnhalbachse ist.
Das erste Keplergesetz legt nahe, die Planetenbahnen durch Polarkoordinaten zu beschreiben:
p
1 + cos φ
mit < 1 als Exzentrität der Ellipse und p > 0 als freiem Parameter.
r=
2
(1)
Zweikörperproblem
Befinden sich zwei Körper in einem System kann die aufeinander wirkende Kraft F zwischen m1
und m2 nur vom Differenzvektor r := r1 − r2 abhängen. Die Bewegungsgleichungen lauten:
m1 r̈1 = F (r, ṙ, t)
(2)
m2 r̈2 = −F (r, ṙ, t)
(3)
Die Bewegung des Zweikörper-Systems kann in die Bewegung des Schwerpunktes
R :=
Z
1
rρ(r)dV =
mgesammt
m1 r1 + m2 r2
m1 + m2
(4)
und in die des Differenzvektors
r = r1 − r2
(5)
zerlegt werden.
Addition der Gleichungen (2) und (3)führt zu
m1 r¨1 + m2 r¨2 = 0
(6)
R̈ = 0
(7)
dh
Die Schwerpunktsbewegung ist gleichförmig und von der Relativbewegung der zwei Massen unabhängig.
2
1
multiplizierten Gleichung (3) und von der mit m1m+m
multiplizierten
Subtraktion der mit m1m+m
2
2
Gleichung (2) ergibt:
m1 m2
r̈ = F(r, ṙ, t)
m1 + m2
3
(8)
wobei
µ=
m1 m2
m1 + m2
(9)
die sogenannte reduzierte Masse ist. Somit kann man die Relativbewegung der beiden Massen durch
die der Bewegung einer reduzierten Masse beschreiben.
Die Bewegungen der einzelnen Massen ergeben sich wieder aus R(t) und r(t):
3
r1 (t) = R(t) +
m2
r(t)
m1 + m2
(10)
r2 (t) = R(t) −
m1
r(t)
m1 + m2
(11)
Zentralkräfte
Von besonderer Bedeutung sind Zentralkräfte F(r, t), Kräfte, die immer auf einen bestimmten
Punkt r0 , das sog Zentralkraftzentrum“ zeigen. Dieses legen wir in den Ursprung des Koordina”
tensystems. Das heißt sie lauten
F(r, t) = f (r, t)
r
r
(12)
wobei r = |r| und f (r, t) eine beliebige skalare Funktion ist.
Hat das Zentralkraftfeld einen festen Ursprung, ist der Drehimplus L = r × p erhalten, wenn der
Anfang des Ortsvektors im Kraftzentrum liegt:
d
d
L = (r × mṙ) = m(ṙ × ṙ + r × r̈) = mr × r̈ = r × F = 0
dt
dt
(13)
Außerdem verlaufen Zentralkraftbewegungen in der Ebene, weil
r · L = r · (r × p) = 0
(14)
Zentralkräfte sind genau dann konservativ, also haben ein Potential, wenn sie kugelssymmetrisch
sind.
Beweis:
Die Aussage lässt sich am besten mit der Aussage beweisen, dass eine Kraft genau dann konservativ
ist, wenn sie rotationssymmetrisch ist, also ihre Rotation verschwindet:
f (r, t)
f (r, t)
r
rot[f (r, t) ] =
rot r + [grad
]×r
r
r
r
(15)
Wegen rotr = 0 ist der erste Term null und die Rotation der Zentralkraft verschwindet genau
und daher senkrecht auf den Äuipotentialflächen
dann, wenn der Ortsvektor rparallel zu grad f (r,t)
r
steht. Folglich sind Zentralkräfte nur für kugelförmige Äquipotnetialflächen konservativ. Die skalare
4
Funktion f kann nicht von der Richtung abhängen und hat die Form f = f (r, t).
Zur weitern Vereinfachung lassen wir die explizite Zeitabhängigkeit fallen und kommen auf zentralkräfte, denen Größe nur vom Abstand r vom Zentrum abhängt:
F(r) = f (r)
r
r
Das dazugehörende Potential V kann ebenso nur von r abhängen:
p
V = V ( x2 + y 2 + z 2 ) = V (r)
p
dV (r) r
F(r) = −V ( x2 + y 2 + z 2 ) = −
dr r
4
(16)
(17)
(18)
Bewegungen im konservativen Zentralkraftfeld
Im konservativen Zentralkraftfeld ist die Energie in Form eines stetigen Potentials eine Erhaltungsgröße:
E=
m ˙2
(r + r2 φ̇2 ) + V (r)
2
(19)
Eine zweite Erhaltungsgröße ist der Drehimpuls L:
L = mr2 φ̇ = const
(20)
Dies ergibt sich aus dem 2. Keplergesetz:
dA
1 dφ
L
= r2
=
= const
dt
2 dt
2m
(21)
Von besonderm Interesse sind: die Radialbewegung r(t), die Winkeländerung φ(t) und die Bahngleichung r(φ).
Diese lassen sich mittels der Energie und Impluserhaltung und den daraus folgenden Differentialgleichungen bestimmen.
φ̇ =
L
m r2
(22)
eingesetzt in Gleichung (19) ergibt eine Bewegungsgleichung für r(t):
E=
m 2
L2
ṙ +
+ V (r)
2
2mr2
Nach ṙ aufgelöst ergibt sich:
5
(23)
r
L2
dr
2
)
=±
(E − V (r) −
dt
m
2mr2
(24)
Läuft das Teilchen vom Koordinatenursprung weg ist ṙ positiv, läuft es weg ist ṙ negativ. Für ṙ = 0,
sprich
V (r) +
L2
=E
2mr2
(25)
haben wir Umkehrpunkte der Radialbewegung.
Mit r(t = 0) = r0 ergibt Integration
dr0
r
Z
t =±
q
r0
2
m (E
− V
(r0 )
−
L2
)
2mr02
dx
(26)
Die Radialbewegung r = r(t) erhält man über die Umkehrfunktion.
Setzt man dies nun in
φ̇ =
dφ
L
=
dt
mr(t)2
(27)
mit φ(t = 0) = φ0 ein erhält man φ(t)
L
φ(t) =
m
t
Z
0
dt0
+ φ0
r2 (t0 )
(28)
Möchte man die geometrische Bahn, verfährt man wie folgt:
dt =
dt = ± q
m 2
r dφ
L
(29)
dr
2
m (E
− V (r0 ) −
(30)
L2
)
2mr02
Gleichsetzen, dann integrieren und man erhält:
L
φ(r) = ±
m
Z
dr0
r
r0
r02
q
2
m (E
V (r0 ) −
L2
)
2mr02
+ φ0
(31)
Die Umkehrfunktion dazu liefert die Bahngleichung r(φ).
Setzt man nun zum Beispiel für das Potential das Keplerpotential ein (s.Übung), erhält man die
Bahngleichung
r =
p
1 + cos(φ − φ0 )
6
(32)
Der Winkel φ0 geht in die Richtung, in welcher die Planetenbahn dem Brennpunkt (hier der Sonne)
am nähesten ist, in Richtung Perihel.
Gegenüber des Perihels befindet sich das Aphel.
Man erhält vier mögliche Bahnformen:
1)Für = 0 liegt eine Kreisbahn vor mit Radius
R=p=
p2φ
(33)
mα
(wegen (32)) und mit Energie
1
α
α
E = mv 2 − = −
2
R
2R
(34)
Der Betrag der negativen Energie ist proportional zum Bahnradius R.
2) Für 0 < < 1 läuft das Teilchen auf einer Ellipse. Die Abstände des rP des Perihels und rA des
Aphels vom Koordinatenursprung sind nach Gl .(32)
rP =
p
p
rA =
1+
1−
(35)
Die große Halbachse a ist
a = rP + rA =
p
−α
=
2
1−
2E
(36)
nach
p :=
p2φ
mα
r
:=
1+
2EL2
mα2
3) Für = 1 läuft das Teilchen auf einer Parabel mit Perihelabstand rp =
p
Teilchen auf einer Hyperbel mit Perihelabstand rp = 1+
5
(37)
p
2
4) Für > 1 läuft das
Lenzscher Vektor
~
Vom Brennpunkt aus zeigt in Richtung Perihel der Lenzsche Vektor Λ.
~ = p×L − r
Λ
mα
r
(38)
Unter allen Zentralkraftpotentialen hat nur das Keplerpotential neben Energie E und Drehimplus
L eine weitere Erhaltungsgröße - den Lenzschen Vektor!
~
dΛ
d p×L
d r
=
−
dt
dt m α
dt r
7
(39)
d p×L
ṗ × (r × p)
(ṗ · p)r (ṗ · r)p
=
=
−
dt m α
mα
mα
mα
(40)
Die zeitliche Ableitung vom Drehimpuls L fällt weg, da dieser eine Erhaltungsgröße ist.
d r
ṙ
r
p
r
r
p
r · (p · r)
= − 2 · ṙ =
− 2 · ṙ · =
−
dt r
r r
mr r
r
mr
mr3
(41)
Mit
mr̈ = ṗ = −α
r
r3
(42)
ist gezeigt:
~
dΛ
= 0
dt
6
(43)
Effektives Potential
Da die Berechnung der Potentiale sich normalerweise schwieriger gestaltet, führt man das effektive
Potential ein, um qualitative Aussagen treffen zu können.
p2φ
m 2
m
E = ṙ + V (r) +
=: ṙ2 + Vef f (r)
2
2mr2
2
(44)
Anhand der graphischen Darstellung von Vef f ist eine qualitative Disskusion der radialen Bahnbewegung möglich.
7
Corioliskraft, Zentrifugalkraft
Transformiert man sein Koordinatensystem von einem Inertialsystem S in ein sich mit der Winkelgeschwindigkeit ω bewegegendes System S’, führt dies zu einer neuen Geschwindigkeit v 0 = v−ω×r.
Diese Geschwindigkeit v’ hat Scheinkräfte zur Folge - die Corioliskraft (2m~
ω × v’) und die Fliehkraft (m~
ω × (~
ω × r)). Beide errechnen sich am besten aus Lagrange und mit ihnen ist die
Gesamtkraft in einem gleichförmig rotierenden System S’
m a0 = −
∂V
− 2m~
ω × v’ − m~
ω × (~
ω × r)
∂r
8
(45)