I. Der Zeeman Effekt

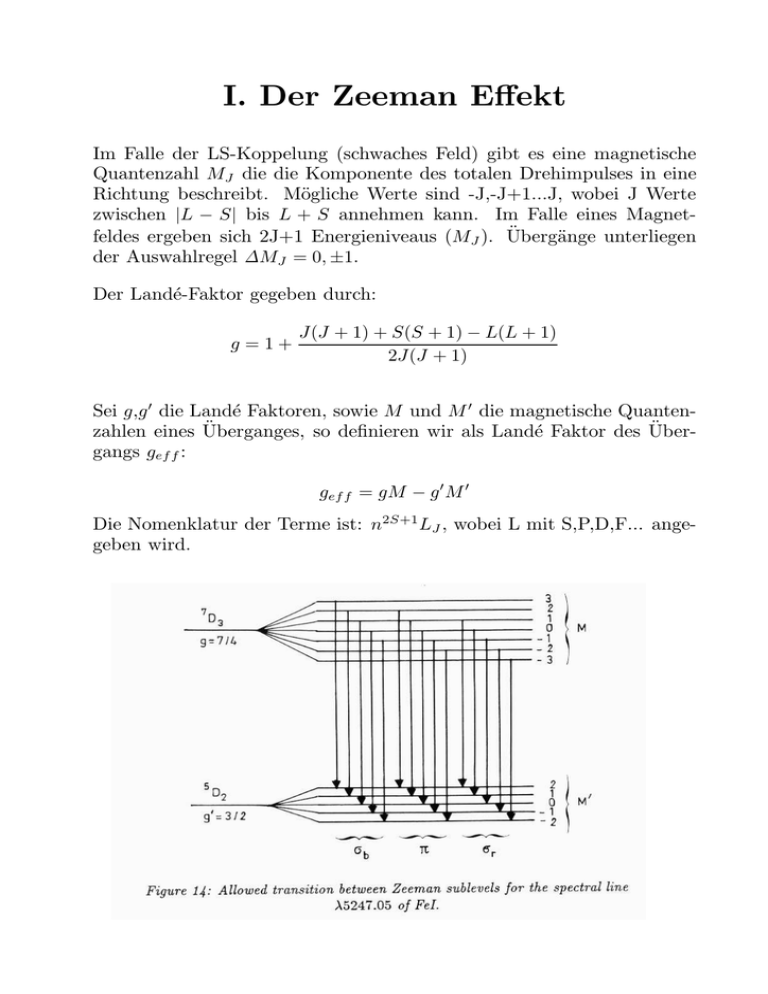
I. Der Zeeman Effekt
Im Falle der LS-Koppelung (schwaches Feld) gibt es eine magnetische
Quantenzahl MJ die die Komponente des totalen Drehimpulses in eine
Richtung beschreibt. Mögliche Werte sind -J,-J+1...J, wobei J Werte
zwischen |L − S| bis L + S annehmen kann. Im Falle eines Magnetfeldes ergeben sich 2J+1 Energieniveaus (MJ ). Übergänge unterliegen
der Auswahlregel ∆MJ = 0, ±1.
Der Landé-Faktor gegeben durch:
g =1+
J(J + 1) + S(S + 1) − L(L + 1)
2J(J + 1)
Sei g ,g 0 die Landé Faktoren, sowie M und M 0 die magnetische Quantenzahlen eines Überganges, so definieren wir als Landé Faktor des Übergangs gef f :
gef f = gM − g 0 M 0
Die Nomenklatur der Terme ist: n2S+1 LJ , wobei L mit S,P,D,F... angegeben wird.
II. Die Stokes Parameter
Stellen wir uns eine monochromatische elektromagnetische Welle die sich
in z -Richtung ausbreitet vor:
Ex = ξx cosφ
Ey = ξy cos(φ + )
wobei φ = ωt − kz und die Phasendifferenz zwischen Ex und Ey ist. ξx
und ξy sind die Amplituden und beschreibt die (elliptische) Polarisation.
I = hξx2 + ξy2 i
Q = hξx2 − ξy2 i
U = 2hξx ξy cosi
V = 2hξx ξy sini
Für nichtpolarisierte Strahlung gilt Q=U=V=0. Für vollständig polarisierte Strahlung gilt I 2 = Q2 + U 2 + V 2 . Der Grad der Polarisation kann
beschrieben werden durch:
r
Q2 + U 2 + V 2
P =
I2
Die π -Komponenten: ∆MJ = 0 sind linear polarisiert. Beobachten wir
parallel zu den magnetischen Feldlinien, so ist Q 6= 0, U 6= 0.
σ -Komponenten: ∆MJ = ±1 sind zirkular polarisiert. Bei Beobachtungen “entlang” der Feldlinien ist V 6= 0.
II. Felder in leitender Materie
IIa. Unos Gleichung
Für den Strahlungstransport und die Emission einer magnetischen Atmopshäre brauchen wir eine neue Strahlungstransportgleichung, dies ist
Unos Gleichung: Diese Gleichung ist ähnlich der bisherigen Strahlungstransportgleichung nur ist jetzt die Intensität durch den Vektor der
Stokesparameter ersetzt.
cosθ
dI
= (1 + η)(I Bλ,T )
dτ
wobei θ der Winkel zur vertikalen Richtung, τ die optische Tiefe und
Bλ die Kirchhoff-Planck Funktion (lokales thermodynamisches Gleichgewicht) ist.
I ist jetzt ein Vektor der die Stokes-Parameter enthält und η ist eine
Matrix.

I
Q
I= 
U
V

ηI
η
η= Q
ηU
ηV

ηQ
ηI
0
0
ηU
0
ηI
0

ηV
0 

0
ηI
Sei γ und φ die Inklination und der Azimuth der magnetischen Feldlinien
relativ zur Sichtlinie und η die drei Absorptionskoeffizienten:
1
1
ηsin2 γ + (η + + η − )(1 + cos2 γ)
2
4
1
1
ηQ = [ η − (η + + η − )]sin2 γ + cos2φ
2
4
1
1
ηU = [ η − (η + + η − )]sin2 γ + sin2φ
2
4
1
ηV = (η + + η − )cosγ
2
ηI =
IIb. Ein Beispiel
Betrachten wir die FeI 5250.2 Å Linie und nehmen an dass die Spektrallinien gaussförmig und das Feld schwach sei (Gef f = 3; ohne Feld
wäre die Breite der Linie ∆λD = 42mÅ und die zentrale Tiefe r0 = 0.7),
so ergibt sich:
V
= 9.6 10−4 B [Gauss] cosγ
I
Ein Feld von 10 Gauss würde zu einer zirkularen Polarisation von 1%
führen. Um die wahre Richtung der Feldlinie zu bestimmen brauchen
wir noch Q und U:
Q
≈ 10−6 B 2 [Gauss] sin2 γ
I
Im Falle des 10-Gauss-Feldes ergäbe sich ein lineare Polarisation von nur
0.1% .
IIc. Die eingefrorenen Feldlinien
Die elektrische Leitfähigkeit kann für den Fall kleiner Ionisation (Elektronendichte kleiner als die Dichte der neutralen Teilchen ne ≤ nn ) mit der
Gleichung von Nagasawa (1955) abgeleitet werden. In der Photosphäre
und der unteren Chromosphäre liegt der Wasserstoff und das Helium in
der Tat hauptsächlich in neutraler Form vor. Schwere Elemente sind eine
Quelle von Elektronen. Für diesen Fall leitet Nagasawa ein Gleichung
für die elektrische Leitfähigkeit her:
3e2
ne
σ=
8S(2πme kT )1/2 nn
Wobei S der Wirkungsquerschnitt der Kollision zwischen Elektronen und
neutralen Teilchen ist. Typische Werte der Leitfähigkeit in der Photosphäre liegen bei 100 bis 1000 Ohm−1 m. Die Leitfähigkeit der Materie
in einem Sonnenfleck ist ein bißchen kleiner, da die Temperatur etwas
kleiner ist.
Bedenken wir die Größe der Strukturen, so ist der elektrischen Widerstand in der Photosphäre sehr klein.
Im Falle unendlicher Leitfähigkeit sind die Feldlinien in der Materie
“eingefroren”. Strömungen der Materie folgen dann immer den Feldlinien.
III. Magnetische Flußröhren
Viele Leute glauben, daß alle Regionen mit starken Magnetfeldern auf
der Sonne dunkle Sonnenflecken sind. Dem ist nicht so, es gibt auch
helle Flecken, die magnetische Flußröhren. Sprechen wir also zunächst
über die hellen Flußröhren.
Da die Feldlinien an der Materie kleben, werden sie in konvektiven Regionen in die Abstömenden Bereichen gespühlt (intergranulare Zwischenräume). Dies hat Parker schon 1963 sich so vermutet. Wie aber sehen
die Flußrören aus?
Phänomenologie:
Filigree in Hα (Dunn & Zirker 1973): Verwenden wir eine Hα-Schmalbandfilter und verschieben die Wellenlänge vom Linienzentrum um ∆λ =
2 Å in die Linienflügel, so sehen wir helle Körner, das Filigree, deren
Durchmesser einige hundert km beträgt. Bei dieser Wellenlänge beobachten wir eine Regionen, die einige hundert km oberhalb der Photosphäre ist. Das Filigree befindet sich offenbar oberhalb der intergranularen Zwischenräume. Wird das Filigree auf gleiche Art und Weise mit
einem CaII-Filter beobachtet, so schimpft es sich ”Crinkles’.
Facular Points am Sonnenrand (Mehltretter 1974): Wegen der MitteRand Variation der Sonne sehen wir bei Beobachtungen am Sonnenrand
auch in höhere Schichten der Sonnenatmosphäre als bei Beobachtungen im Sonnenzentrum. Seit langer Zeit waren die sogenannten Fackeln bekannt, die häufig in der Nähe von Sonnenflecken zu sehen waren
(Beobachten wir sie in CaII, so heißen sie Plage-Regionen). Beobachtungen von Mehltretter zeigten nun, dass die Fackeln aus vielen kleinen
Punkten bestehen, die er Facular Points nannte. Auch diese befinden
sich wieder oberhalb der intergranularen Zwischenräume. Beobachtungen in Hα und CaII zeigen, dass sie etwa mit dem ‘’Filigree ‘’ und den
”Crinkles” zu tun haben.
Facular Points in der Sonnenmitte: Beobachtungen mit sehr hoher
räumlichen Auflösung zeigen nun, dass die Facular Points auch als sehr
kleine (100-200 km) Punkte in der Sonnenmitte zu sehen sind.
Dünne Flußröhren:
Was ist nun los? Leider ist es bis jetzt nicht möglich, die magnetische
Feldstärke in einem 100x100 km kleinen Gebiet zu messen.
Es gibt aber einen Ausweg: Wir können einfach die Feldstärken in einem
großen Gebiet messen und dann zählen wieviele Facular Points in diesem
Gebiet sind. In der Tat gibt es eine sehr gute Korrelation zwischen
dem totalen magnetischen Fluß und der Anzahl der Facular Points. Ein
Facular Point hat etwa 4.4 109 Wb (großer Sonnenfleck ≈ 1014 Wb).
Damit ist die magnetischen Flußdichte etwa 1000-2000 Gauss und damit
nur nicht viel kleiner als die eines Flecks.
Warum sind die Flußröhren hell?
Der Grund ist der folgende:
· sie sind kühler als die Umgebung bei gleicher geometrischer Höhe,
aber
· die Atmosphäre in der Röhre ist durchsichtiger weil die Gasdichte
in der Röhre kleiner ist.
· Die Dichte ist kleiner, da innen der Gasdruck und der magnetische
Druck wirkt, außen aber nur der Gasdruck. Innen herrscht also ein
kleinerer Gasdruck und damit ist auch die Gasdichte kleiner.
· Weil die Röhren so dünn sind gelangt relativ viel Licht aus der
heißeren Umgebung in die Röhre und wird nach außen gestreut.
· Flußröhren sind damit bei gleicher geometrischer Tiefe zwar kühler
als die Umgebung, aber bei gleicher optischen Tiefe aber heißer als
die Umgebung.
Der magnetischen Fluß:
Wie bereits erwähnt, gibt es auf der Sonne kleine (Flußröhren) und große
Regionen (Flecken) mit magnetischen Fluß. Es zeigt sich, dass weder
die kleinen Flußröhren, noch die großen Flecken den größten Beitrag
zum magnetischen Flusß der Sonne liefern. Den größten Beitrag liefern
Strukturen mittlerer Größe, die Mikroporen (Durchmesser 350–650 km).
IV. Flecken
Sonnenflecken sind die auffäligsten Erscheinungen aktiver Regionen.
Flecken treten immer in bipolaren Gruppen auf, bei denen der eine Teil
ein magnetischer Nordpol, der andere ein magnetischer Südpol ist. Der
vorauseilende Fleck ist stets etwas dichter am Äquator als der nacheilende. Flecken befinden sich in geographischen Breiten von 10 bis 40 Grad.
Hier ist eine Magnetogramm der Sonnenscheibe:
Größenverhältnisse:
· Flußröhren haben einen Durchmesser von 100-200 km, in aktiven
Regionen klumpen sie zusammen um gröss ere Flußkonzentrationen
zu bilden.
· Flußkonzentrationen mit einem Durchmesser von einigen 100 km im
Durchmesser heißen Poren.
· Wenn die Poren eine Größen von 2400 km haben, entwickelt sich eine
Penumbra. Wir sprechen dann von einem Sonnenfleck mit Umbra
und Penumbra.
Sonnenflecken wachsen für einige Tage und verschwinden dann wieder
langsam.
Die Größten Sonnenflecken existieren für einige Wochen. Sonnenflecken haben Größen von 2500 km bis 50000 km. Sie sind also immer
noch klein im Vergleich zur Sonne, die ein Durchmesser von 1392000 km
hat.
Sonnenfleckenflächen werden meist als 1./1000000. der Sonnenoberfläche
angegeben. Im Maximum der Sonnenfleckenaktivität bedecken die Flecken eine Fläche von nur 0.3%.
Einiges über die Flecken:
Sind Flecken wirklich dunkel? Die Temperatur der Flecken beträgt
3500 K, die der umgebenden Photosphäre 5780 K. Ein Fleck mit einem
Durchmesser von 2400 km hätte immerhin ein Helligkeit von -11 mag,
wäre also nur 1.7 mag schwächer, als der Vollmond! Im Grunde sind
auch die Flecken hell!
Warum sind Flecken kühler als die umgebende Photosphäre? Das starke
Feld eines Flecks behindert den konvektiven Energietransport.
Wie sieht das Spektrum eines Flecks aus? Mit dem 1-m FTS des McMath
wurde ein Spektralatlas eines typischen Sonnenflecks aufgenommen. Er
hat eine magnetische Feldstärke von ≈ 3000 Gauss und einen Spektraltyp
M2 bis M5.
Wilson Effekt: Da das Plasma eines Flecks ein bißchen durchsichtiger
ist als die der Photosphäre, sehen wir in einem Fleck tiefer in die Sonne
hinein (Wilson Depression).
Penumbra: Große Flecken sind von einer Penumbra umgeben. Wären
die Feldlinien in der Umbra im wesentlichen vertikal verlaufen, verlaufen
die der Penumbra in wesentlichen horizontal.
Umbrale Flecken, und penumbrale Körner: Der konvektiven Energietransport ist in einem Fleck nicht total zum erliegen gekommen. Es
gibt einen Rest von Konvektion, der in der Umbra als hellen Flecken und
in der Penumbra als helle Körner zu sehen ist. Umbrale Flecken haben
eine Größe von 200 bis 700 km, die magnetische Feldstärke ist kleiner als
die der Umbra. Die Größe der penumbralen Körner beträgt 300x1500
km, auch sie haben ein kleineres Feld als ihre Umgebung.
V. Evershed-Effekt
Spektren der Penumbra zeigen in starken Linien (Entstehung hoch in
der Atmosphäre) eine ausströmende von Materie (Evershed-Effekt). Wo
fließt die Materie hin ?
Bei Beobachtungen in schwachen Linien, die in nur geringer Höhe über
der Photosphäre entstehen, zeigen sich außer der Ausströmung am Rand
der Penumbra eine Abströmung. Die Materie fließt also zurück in die
Sonne.
Die Abbildung zeigt die Plasmaströmungen in der C 5380 Å-Linie die
in nur geringem Abstand über der Photosphäre entsteht. Materie, die
wieder in die Sonne hineinfließt ist Rot dargestellt.