Zusammenfassung des Seminarvortrags zum Thema Supraleitung

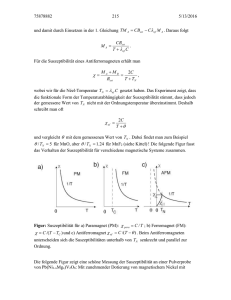
Zusammenfassung des Seminarvortrags zum Thema
Supraleitung mit Anwendung
von Dominik Will
1
1.1
Kurze Einführung in die Supraleitung
Temperaturabhängigkeit des elektrischen Widerstandes bei niedrigen Temperaturen
Nach der klassischen Theorie ist bei niedrigen Temperaturen eine parabolische Abnahme des spezifischen Widerstandes, wie sie
Abbildung 1 zeigt, zu erwarten, wobei der Widerstand am absoluten Nullpunkt einen gewissen Restwert annimmt, der nur von der
Streuung der Leitungselektronen an Verunreinigungen herrührt.
1911 Beobachtete jedoch Kamerlingh Onnes bei Quecksilber bei
einer Temperatur von etwa 4 K, der sog. kritischen Temperatur,
ein rapides Abfallen des elektrischen Widerstandes und er konnte
unterhalb dieser Temperatur keinen Widerstand mehr nachweisen, d.h. der Stromtransport erfolgte widerstandsfrei. Entsprechend nannte er dieses Phänomen Supraleitung im Gegensatz Abbildung 1: typischer Wizur Normalleitung, wie man sie nach der klassischen Theorie er- derstandsverlauf eines Mewartet und wie man sie auch bei einigen anderen Elementen, die talls in Abhängigkeit von der
keine Supraleitung aufweisen, vorfindet.
Temperatur
Die meisten Elemente weisen Supraleitung auf mit kritischen
Temperaturen von wenigen Millikelvin bis hin zu fast 10 Kelvin. Manche Elemente werden
erst unter großem Druck supraleitend. Der große Durchbruch gelang jedoch in den achtziger
Jahren mit der Entdeckung sog. Hochtemperatursupraleiter (HTS), die auf oxidischen Verbindungen basieren und kritische Temperaturen von bis zu 135 K unter Normalbedingungen bzw.
165 K unter Druck erreichen.
1.2
Wie misst man Supraleitung
Die beste experimentelle Möglichkeit, das vollständige Verschwinden des elektrischen Widerstandes zu überprüfen, ist der Nachweis sog. permanenter Supraströme. Dazu setzt man eine
Schleife aus supraleitendem Material oberhalb der kritischen Temperatur einem äußeren Magnetfeld aus, das einen magnetischen Fluss durch die Schleife bewirkt, kühlt sie anschließend
unter die kritische Temperatur ab und schaltet das äußere Magnetfeld ab. Aufgrund der unendlichen Leitfähigkeit σ = ∞ der Leiterschleife, aber der nur endlichen Stromdichte j < ∞, von
der sie aufgrund der endlichen Zahl von Ladungsträgern durchsetzt werden kann, folgt aus der
~ dass das elektrische Feld E
~ in der supraleitenden Leiterschleife
Konstitutionsgleichung ~j = σ E,
0 sein muss. Da jedoch ein Abklingen des zuvor erzeugten Flusses durch die Schleife ein elektrisches Feld nach dem Induktionsgesetz induzieren müsste, kann der Fluss nicht abnehmen und
in der Leiterschleife wird ein permanenter Suprastrom angeworfen, der ein eigenes Magnetfeld
1
Supraleitung mit Anwendung
2
erzeugt und somit den Fluss durch die Schleife aufrecht erhält.
Mit dieser Methode konnte gezeigt werden, dass der elektrische Widerstand bei der kritischen
Temperatur um mindestens 14 Größenordnungen abfällt. 14 Größenordnungen im elektrischen
Widerstand trennen z.B. auch Isolatoren von gewöhnlichen Leitern wie Kupfer.
1.3
Der Meissner-Ochsenfeld-Effekt
Wie wir im vorigen Abschnitt gesehen haben, kann sich in einem Supraleiter der magnetische
Fluss nicht ändern. Daher kann ein Magentfeld auch nicht in einen Supraleiter eindringen.
Was passiert jedoch, wenn in einem Supraleiter bereits ein Magnetfeld vorhanden ist, wenn
er z.B. durch Abkühlung supraleitend wird? Die Antwort ist, dass er das magnetische Feld
schlagartig aus seinem Inneren verdrängt. Da dies nicht allein aus der Eigenschaft σ = ∞ folgt
– das Magnetfeld könnte ja auch quasi eingefroren“ werden und sich nicht mehr verändern –,
”
bezeichnet man dieses Phänomen auch als den Meisner-Ochsenfeld-Effekt.
1.4
Supraleitung als perfekter Diamagnetismus
Das Magnetfeld im Inneren von Materie setzt sich aus einem Beitrag der magnetischen Erre~ = µ0 (H
~ +M
~ ). Da im Innegung H und der Magnetisierung der Materie M zusammen: B
ren eines Supraleiters das Magnetfeld 0 sein muss, folgt für seine magnetische Suszeptibiltät:
χ := (dM/dH)H=0 = −1
Man spricht daher im Zusammenhang mit Supraleitung auch von perfektem Diamagnetismus.
1.5
Die London-Gleichungen
Die theoretische Beschreibung der Supraleitung stellen die sog. London-Gleichungen dar. Sie
wurden zunächst rein empirisch motiviert und erst im Nachhinein in den fünfziger Jahren im
Rahmen der sog. BCS-Theorie abgeleitet. Sie ergeben sich aus der Gleichung
2
~,
~j = − nS e A
me
(1)
wobei nS die Dichte der supraleitenden Elektronen, die i.A. nur einen kleinen Teil der gesam~ das elektromagnetische Vektorpotential ist. Ableiten Leitungselektronen ausmachen, und A
˙ = ns e2 E
˙ = eE
~ ⇒ me~v
~
ten dieser Gleichung nach der Zeit liefert die 1. London-Gleichung ~j
me
(~j = nS e~v ), die besagt, dass supraleitende Elektronen in einem elektrischen Feld gleichmäßig,
d.h. ohne Widerstand, beschleunigt werden. Durch Rotationsbildung in (1) erhält man die 2.
2
~ ⇒ ∆B
~ = λ2 B
~ mit λ = ( me 2 ) 12 , die besagt, dass ein äußeLondon-Gleichung rot~j = − nmS ee B
µ0 nS e
res Magnetfeld zum Inneren eines Supraleiters hin über die Strecke λ auf einen Bruchteil e−1
exponetiell abfällt,
¡ x ¢ denn z.B. eine eindimensionale Lösung dieser Gleichung ist offensichtlich
B(x) = B0 exp λ . Dies ist gerade der Meissner-Ochsenfeld-Effekt.
1.6
Typ 1 und Typ 2 Supraleiter
Der physikalische Grund für das Auftreten von Supraleitung ist, dass durch das Atomrumpfgitter vermittelt eine attraktive Wechselwirkung zwischen Leitungselektronen existiert. Daher ist
es für die Elektronen energetisch günstiger, sich zu sog. Cooper-Paaren zusammenschließen, deren gemeinsame Wellenfunktion eine Ausdehnung von bis zu 1000 nm hat, sodass diese CooperPaare über viele Gitterperioden hinweg miteinander überlappen. Dies ist nur dadurch möglich,
dass die Cooper-Paare bosonisch sind und daher für sie das Pauli-Verbot nicht mehr gilt. Beim
Eintreten von Supraleitung findet daher so etwas Ähnliches wie Bose-Einstein-Kondensation
Supraleitung mit Anwendung
3
statt und ein Teil der Leitungselektronen kondensiert“ in einer einzigen kohärenten Welle von
”
Cooper-Paaren im energetisch niedrigsten Quantenzustand. Die Dichte dieser Cooper-Paare
baut sich über eine charakteristische Strecke ξ, die sog. Kohärenzlänge, hinweg auf.
Setzt man nun einen Supraleiter einem äußerem Feld aus, dass immer stärker wird, so ist klar,
dass der Supraleiter nur bis zu einer gewissen Feldstärke, der sog. kritischen Feldstärke BC , ausreichend Abschirmungsströme aufbauen kann, um das Feld aus seinem Inneren zu verdrängen.
Was dann jedoch genau passiert, hängt davon ab, ob die Ausbildung von Grenzschichten zwischen Normalleitung und Supraleitung energetisch günstig ist oder nicht. Energetisch ungünstig ist sie, wenn für das Aufbrechen der Cooper-Paare mehr Energie benötigt wird, als durch
das Eindringen
des Feldes in den√Supraleiter freigesetzt wird. Dies ist gerade dann der Fall,
√
wenn ξ > 2λ gilt. (Der Faktor 2 ergibt sich nach der Ginzburg-Landau-Theorie für Phasenübergänge aus der dreidimensionalen Geometrie einer solchen Grenzschicht.) In diesem Fall
dringt das äußere Feld bei einer kritischen Stärke BC schlagartig in den gesamten Supraleiter
ein und zerstört die Supraleitung.
Solche Supraleiter bezeichnet man als Supraleiter vom Typ 1.
√
Da es im anderen Fall ξ < 2λ energetisch günstig
ist, Grenzschichten auszubilden, dringt das Feld bereits ab einer relativ kleinen Feldstärke BC1 gebündelt
in Form sog. Flussschläuche oder Vortices ein, um die
kleine ringförmige Supraströme fließen, die das Feld
zum Übrigen des Supraleiters hin abschirmen. Erst
ab einer i.A. sehr viel größeren kritischen Feldstärke
BC2 kann das Feld gar nicht mehr aus dem Inneren
verdrängt werden und die Supraleitung bricht zusammen. Solche Supraleiter bezeichnet man als Supraleiter vom Typ 2 und die Phase teilweisen Eindrin- Abbildung 2: Bei Typ 2 Supraleitern
gens des äußeren Feldes zwischen BC1 und BC2 als dringt ein äußeres Feld in Form sog.
Abrikosov - oder Shubnikov-Phase im Gegensatz zur Vortices ein, von denen jeder ein eleMeissner-Phase unterhalb von BC1 , in der das Feld mentares Flussquant Φ0 trägt.
aus dem Inneren noch vollständig verdrängt wird, also der vollständige Meissner-Ochsenfeld-Effekt gegeben ist.
Da sich in der Abrikosov-Phase die Flussschläuche, in Form derer das äußere Feld eindringt, gegenseitig abstoßen, bilden sie ein regelmäßiges Dreiecksgitter aus. Außerdem trägt jeder dieser
h
.
Flusschläuche ein elementares Quant Φ0 des magnetischen Flusses von 2e
2
2.1
Anwendung in Form von Kabeln aus supraleitendem
Material zum Transport großer Ströme
Harte Supraleiter bzw. Supraleiter vom Typ 3
Da in Typ 1 Supraleitern ein Strom nur in einer dünnen Grenzschicht an der Leiteroberfläche
fließen kann, weil das von ihm erzeugte Magnetfeld aus dem Supraleiter herausgedrückt wird,
zeigt eine Beispielrechnung auf Basis des Ampère’schen Durchflutungsgesetztes, dass man mit
Typ 1 Suprleitern nur relativ bescheidene Stromdichten erzielen kann. Als technische Supraleiter eignen sich daher zwangsläufig nur Typ 2 Supraleiter in der Abrikosov-Phase. Auf die
in der Abrikosov-Phase eindringenden Flussschläuche wirkt jedoch, wenn ein Transportstrom
durch den Supraleiter fließt, eine Lorentz-Kraft, die dazu führt, dass sich die Flussschläuche
senkrecht zum Transportstrom bewegen, es kommt zu sog. Flussfließen. Da dieses Flussfließen
mit Dissipation verbunden ist, ist a priori nicht klar, wie in der Abrikosov-Phase verlustfreier
Stromtransport im Supraleiter möglich ist.
Supraleitung mit Anwendung
4
Die Lösung des Problems ist, dass man
die Flussschläuche an sog. Pinningzentren fixiert, die man in Form von normalleitenden Ausscheidungen, Versetzungen
oder Korngrenzen realisiert, an denen
sich die Flussschläuche bevorzugt, d.h.
mit weniger Energieaufwand, anlagern
können. Die Flussschlauchfixierung funktioniert natürlich genau dann, wenn die
auf die Flussschläuche wirkende LorentzKraft höchstens so groß ist wie die Pinningkraft. Daraus ergibt sich eine obere
Schranke für die Transportstromdichte,
fP
die sog. kritische Stromdichte jC = Φ
,
0
wobei fP die Pinningkraftdichte ist, also Abbildung 3: Flussschläuche lagern sich in einem
Pinningkraft pro Flussschlauchlänge.
Typ 3 Supraleiter bevorzugt an Pinningzentren an.
Solche Supraleiter vom Typ 2 mit Pinningzentren bezeichnet man auch als Typ 3 Supraleiter oder harte Supraleiter, da ihre Magnetisierungskurve eine Hysterese aufweist, weil beim Ummagnetisieren Flussschläuche von
Pinningzentren entfernt werden müssen, was mit Dissipation verbunden ist.
2.2
Die kritischen Größen bei einem Supraleiter
Insgesamt gibt es also drei kritische Größen bei einem
Supraleiter: Erstens die kritische Temperatur, zweitens
die kritische Feldstärke BC bzw. BC1 und BC2 und drittens die kritische Stromdichte jC . Alle drei stehen in
einem funktionalen Zusammenhang, der in Abbildung
4 grafisch dargestellt ist. Supraleitung ist nur möglich,
wenn keine der kritischen Größen überschritten wird,
d.h. alle Punkte im Oktanden unterhalb der in Abbildung 4 dargestellten Fläche sind mögliche Arbeitspunkte eines Supraleiters. Ganz allgemein gilt: Wird
einer dieser drei Parameter größer, so werden die kritischen Schwellenwerte für die anderen beiden kleiner.
2.3 Thermische Stabilität von techni- Abbildung 4: Zusammenhang der kritischen Größen bei einem Supraleiter
schen Supraleitern
Auch in einem technischen Supraleiter fließt ein Transportstrom an der Oberfläche. Dort fließt
er mit der maximal möglichen kritischen Stromdichte und dringt nur so weit wie notwendig
ein, um die Stromstärke des gesamten Transportstromes zu gewährleisten. Kommt es nun zu
einer leichten Temperaturerhöhung, so nimmt die kritische Stromdichte ab und der Strom muss
tiefer in den Leiter eindringen, um die gleiche Gesamtstromstärke zu erzielen. Bei diesem Eindringprozess werden neue Flusszentren besetzt und es kommt zu Dissipation. Diese Dissipation
erzeugt wiederum eine weitere Temperaturerhöhe.
Um nun die thermische Stabilität des Supraleiters zu gewährleisten, ist es notwendig, dass
die zweite Temperaturerhöhung nicht größer ist als die erste, da ansonsten im jedem Fall eine
Kettenreaktion einsetzen würde, die zu einer immer größeren Temperaturerhöhung führt, bis
Supraleitung mit Anwendung
5
schließlich die kritische Temperatur überschritten und die Supraleitung zerstört wird. Hinreichend ist diese Bedingung allerdings nicht, vielmehr muss eine Konvergenz zu einem stabilen
Zustand gegeben sein. Allerdings ergibt sich bereits aus jener notwendigen Bedingung, dass der
Strom nur in einer Oberflächenschicht mit begrenzter Dicke erfolgen kann, also genauso wie
beim Typ 1 Supraleiter. Der entscheidende Unterschied ist jedoch, dass die kritische Feldstärke
BC2 und damit auch die kritische Stromdichte jC bei einem Typ 2 Supraleiter i.A. wesentlich
größer als BC bzw. jC bei einem Typ 1 Supraleiter ist.
Die Konsequenz bei der Konstruktion technischer Supraleiter ist, dass ein technischer Supraleiter aus möglichst vielen dünnen Filamentdrähten bestehen sollte, da zum Stromtransport
sowieso nur eine dünne Oberflächenschicht beiträgt.
2.4
Kühlung eines technischen Supraleiters
Bei der Kühlung eines Supraleiters hat man das Problem, dass Supraleiter i.A. sehr schlechte
Normalleiter sind. Kommt es an einer Stelle zu einer Störung der Supraleitung und zum Übergang zur Normalleitung, so entsteht bei der Normalleitung eine so große elektrische Verlustleistung, dass die entstehende Wärme über ein Kühlbad nicht in ausreichendem Maße abgeführt
werden kann. Eine einfache Beispielrechnung für NbTi, einen üblichen technischen Supraleiter,
ergibt eine notwendige Temperaturdifferenz zwischen Supraleiter und Kühlbad von mehr als
1000 K.
Die Lösung des Problems ist, dass man den Supraleiter in eine sog. normalleitende Matrix
aus einem Material mit guter thermischer und elektrischer Leitfähigkeit einbettet. Z.B. Kupfer
bietet sich an, bei dem man vier Größenordnungen bei der elektrischen Normalleitfähigkeit im
Vergleich zu NbTi gewinnt, sodass eine Temperaturdifferenz zwischen Matrix und Kühlbad von
unter 1 K ausreichend ist.
2.5
Anwendungsgebiete von Hochstromsupraleitern in der Technik
In den allermeisten Anwendungsfällen dienen Drähte aus supraleitendem Material als Erregerspulen für sehr starke Magnetfelder. Die Anwendung mit dem größten Marktvolumen stellt
sicherlich die Magnetresonanztomographie dar. Das benötigte starke Magnetfeld kann in Verbindung mit einer vertretbar kompakten Bauweise nur durch supraleitende Spulen erzeugt
werden.
Ein anderes großes Anwendungsgebiet sind möglichst starke Ablenkmagneten für Teilchenbeschleuniger. Neben dem ursprünglichen Einsatz in Wissenschaft und Forschung kommen diese
in wachsendem Maße ebenfalls in der Medizin bei der Krebstherapie durch Teilchenbestrahlung
zum Einsatz.
(a) Magnetresonanztomograph
(b) Proton-Zyklotron zur Bestrahlungstherapie
Abbildung 5: Anwendungsbeispiele für Hochstromsupraleiter