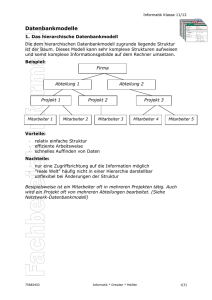
natürliche Join
Werbung

Thema Bedeutung des relationalen Datenbankmodells von Edgar Frank Codd und die Entwicklung der B-Bäume von Rudolf Bayer für die Informatik Matthias Reusche [email protected] B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd Gliederung 1. Einleitung 2. B-Bäume 3. relationales Datenbankmodell 4. Zusammenfassung B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 2 1. Einleitung - Datenbanken sind heutzutage überall anzutreffen Wirtschaft, Forschung und Privathaushalt - den größten Marktanteil haben relationale Datenbanken - in allen Datenbanksystemen werden B-Bäume als Indexstruktur verwendet B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 3 1. Einleitung Prof. Dr. Rudolf Bayer - Geboren am 7.Mai 1939 - Studierte Mathematik in München - 1966 Titel Ph.D. University of Illinois -1972 Ordinarius für Informatik an der TU München - Bundesverdienstkreuz 1. Klasse - SIGMOD Innovations Award 2001 B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 4 1. Einleitung Prof. Dr. Rudolf Bayer (2) - Berater: IBM, Siemens, Amdahl, DEC, Deutsche Telekom - Gastprofessor: IBM, Palo Alto Research Center, Universitäten in Japan, Australien, USA, Singapur - B-Bäume 1969, B*-Bäume, UB-Bäume 90er - Datenbankprotokoll Mehrbenutzertransaktionen 1974 - Organisation und Wartung von großen Indexordnungen - Deutschen Datenschutz - Synchronisation, Parallelisieren und Wiederherstellung von Datenbanken - Expertensysteme - OODBS B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 5 1. Einleitung Dr. Edgar Frank Codd - geboren am 23. August 1923 in Portland - studierte Mathematik in Oxford - 1949 Wissenschaftlicher Mitarbeiter bei IBM - starb am 18. April 2003 in Williams Island - relationales Datenbankmodell 1969 - ALPHA, Rendezvous 1971 - Normalisierungstheorie - Turing-Award 1981 B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 6 2. B-Bäume Beweggründe - neue Märkte für Informatik: Raumfahrt, Industrie und Wirtschaft - 60er erste Direktspeicher - Speicherkapazität begrenzt und teuer - Pseudo-Random-Access-Speicher (Platten, Trommeln) - Überwindung der Zugriffszeit auf eine Seite - Entartungsmöglichkeit anderer Baumarten Methode mit wenig Seitenzugriffen B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 7 2. B-Bäume Definition B-Baum der Klasse τ( k, h) ist entweder ein leerer Baum oder ein geordneter Baum mit folgenden Eigenschaften: - vollkommen ausbalanciert - Knoten hat zwischen k und 2k Einträge (außer Wurzel 1…2k) - Einträge sind geordnet - ein Eintrag besteht aus einem Schlüssel und einem Datum - innere Knoten mit n Einträgen haben n+1 Kindknoten - Kindknoten werden über geordnete Verweise gehalten - Kindknoten enthalten alle >,< Schlüssel B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 8 2. B-Bäume Beispielbaum Für folgende Operationen: Suchen, Einfügen und Löschen - der Klasse τ( 2, 2) Wurzel Blätter - natürliche Zahlen 0, 2, 3, 5, 6, 9, 10, 11, 13, 14, 20, 25, 26, 27 B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 9 2. B-Bäume Suchen in B-Bäumen Erfolgreiches Suchen nach S(13): Nicht jeder Knoten muss vollständig durchgegangen werden B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 10 2. B-Bäume Suchen in B-Bäumen (2) Erfolgloses Suchen nach S(15): Suchkosten: Fmin = 1, Fmax = h, h-1/k ≤ Favg ≤ h-1/2k B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 11 2. B-Bäume Einfügen in B-Bäumen - Zuerst „Zielknoten“ suchen Unterscheidung in 2 Fälle: mit und ohne Splitten - Einfügen S(7) ohne Splitten da noch Plätze im Zielknoten vorhanden B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 12 2. B-Bäume Einfügen in B-Bäumen (2) - Einfügen von S(23) mit Splitten damit Baumeigenschaft erfüllt bleibt - Knoten wird gesplittet und Meridian S(14) an Vaterknoten gegeben B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 13 2. B-Bäume Einfügen in B-Bäumen (3) - Splitten kann iterativ bis zur Wurzel fortgesetzt werden Einfügekosten: Fmin= h und Wmin= 1, Favg= h und Wavg < 1+2/k B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 14 2. B-Bäume Einfügen in B-Bäumen (4) - Einfügen von S(8) , wodurch Baum wächst, da Splitten bis zur Wurzel nötig - Zweiter Knoten und Wurzel wurden gesplittet - Baum wächst an der Wurzel Klasse τ( 2, 3) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 15 2. B-Bäume Löschen in B-Bäumen - Unterscheidung ob Element in einem inneren Knoten oder in einem Blatt ist - Folge des Löschens kann unterbesetzter Knoten sein - Ausgleich mit Nachbarknoten oder Verschmelzung mit Nachbarknoten - Verschmelzung kann iterativ bis zu Wurzel nötig werden nach erster Verschmelzung, löschen S(11) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 16 2. B-Bäume Löschen in B-Bäumen (2) - Verschmelzung auf der 2. Stufe wurde nötig neue Wurzel Klasse τ( 2, 2) nach zweiter Verschmelzung - löschen eines inneren Knotens, erfordert Beibehaltung der Verweise zu den Kindknoten - deshalb muss Element als Ersatz für gelöschtes Element aus dem Kindknoten einspringen - löschen vom inneren Knoten S(10) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 17 2. B-Bäume Löschen in B-Bäumen (3) - S(13) ist aus Kindknoten aufgerückt - andere Möglichkeit mindestens k Elemente zu halten ist der Ausgleich - löschen von S(26) Unterlauf in V4 B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 18 2. B-Bäume Löschen in B-Bäumen (4) - S(23) aus Nachbarknoten wurde zum Ausgleich verwendet Löschkosten: bester Fall Fmin= h und Wmin= 1, obere Schranke Favg ≤ F1+ F2 + F3 < h+1+1/k Wavg ≤ W1+ W2 + W3 < 2+2+1/k = 4+1/k wobei F1, F2, F3 und W1, W2, W3 jeweils die Kostenanteile für Löschen, Ausgleich und Verschmelzen sind B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 19 2. B-Bäume Eigenschaften von B-Bäumen - Knotenanzahl n nach Formel: nmin = 1+2 [(k+1)0+(k+1)1+ ... +(k+1)h-2] = 1+ 2/k[(k+1)h-1-1] - Höhe h entspricht der Gleichung: für n = 0 h=0 für n ≥ 1 log2k+1(n+1) ≤ h ≤ logk+1[(n+1)/2]+1 - gute Skalierbarkeit - gute Abschätzung der Operationskosten - Selbstbalancierend bei jeder Operation - zur Balancierung nur Lokale Betrachtung nötig - Balancierung: unabhängig von Schlüsselmenge oder Einfügereihenfolge - Suchkosten hängen überwiegend von Höhe (!!) des Baumes und nicht von Knotenanzahl ab (k>400 : O(logk n) ) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 20 2. B-Bäume Mentale Hürden des B-Baumes - Speicherausnutzung im „Worst Case“ 50% Realität: 83% - Wachstumseigenschaft von der Wurzel her - Herbst 69 erforscht, aber erst bei E.Knuth 1972 publiziert B*-Baum (hohler Baum) - τ( kn, km, h) - Speicherung der Daten nur noch in Blättern - innere Knoten besitzen nur noch Schlüssel und Verweise - Blätter besitzen Verweise zum Vorgänger und Nachfolgerblatt B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 21 2. B-Bäume B*-Präfix Bäume - auf B* aufbauender Baum - es wird kein vollständiger Schlüssel in den inneren Knoten gespeichert, sondern nur noch Anfang des Schlüssels - Schlüssel in inneren Knoten müssen nicht real sein, sind besser ausbalanciert UB-Bäume Beispiel: 2D - für Multidimensional Indexe (jedes DBS) - Partitionierung mehrdimensionaler Räume durch Raumfüllende Kurve - man erhält lineare Ordnung, welche man in klassischen B-Bäumen ablegt - durch Tupel-Clusterung und Seiten-Clusterung ist Antwortzeit direkt proportional zur Größe der Antwort B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 22 Gliederung 1. Einleitung 2. B-Bäume 3. relationales Datenbankmodell 4. Zusammenfassung B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 23 3. relationales Datenbankmodell Relation - basierte auf mathematischen Grundlagen der relationalen Algebra - Mengen: S1, S2, ... , Sn - Relation R sind alle geordneten Mengen r mit Elementen aus S1×S2×...×Sn - Informationen lassen sich in unterscheidbare Mengen gruppieren und dann als Tupel verwalten (Domain / Entitäten) - Mengen haben Relationen zueinander, welche die Informationen enthalten - Ordnung der Zeilen ist beliebig - Sätze sind verschieden voneinander - Ordnung der Spalten ist wichtig B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 24 3. relationales Datenbankmodell Relation (2) - 80-stellige Relationen nichts ungewöhnliches - Codd fügt dem Domain-Name einen Rollenname hinzu (Bedeutung) - Relation selber besitzt eindeutigen Bezeichner - kein zusammengesetztes Datum im Feld (Atomar) Weitere Konzepte für die Implementierung - Primärschlüssel: eindeutige Identifikation des Satzes (aus 1..n Spalten) - Fremdschlüssel: einbinden von Informationen aus anderer Relation - referentielle Integrität: Beachtung der Datenabhängigkeit B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 25 3. relationales Datenbankmodell Schlüssel Slave Master Satz 2: „Es ist möglich von Dresden nach Leipzig zu fliegen.“ B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 26 3. relationales Datenbankmodell Operationen - Permutation, beliebiges vertauschen der Spalten n! neue Relationen O (a,b,c) P1(a,b,c), P2(a,c,b), P3(b,a,c), P4(b,c,a), P5(c,a,b), P6(c,b,a) - Projektion (Abbildung), Auswahl einer oder mehrerer Spalten Äquivalenter SQL-Code: SELECT Start_Stadt FROM Verbindungen; B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 27 3. relationales Datenbankmodell Operationen (2) - Join (Verbindung) - zwei Relationen R,S haben gemeinsame Domain J = R*S = {(a,b,c):R(a,b)^S(b,c)} J = R*S*T = {(a,b,c,d):R(a,b)^S(b,c)^T(c,d)} - natürliche Join: alle Verbindungen, auch doppelte Äquivalenter SQL-Code: SELECT R.Start_Stadt, S.Ziel_Stadt FROM Verbindungen R, Verbindungen S WHERE R.Ziel_Stadt = S.Start_Stadt; B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 28 3. relationales Datenbankmodell Operationen (3) Beispiel natürlicher Join B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 29 3. relationales Datenbankmodell Operationen (4) - Tie – Operation - verbinden von erster und letzter Spalte, eine Art Hülle bilden (R*) γ(R) = {(a1,a2,...,an-1):R( a1,a2,...,an-1,an) ^ a1=an} - Konstrukt aus dem CODASYL Modell - Komposition - zwei Relationen R,S, dann gibt es K wenn R,S einen Join J haben, so dass K = Projektion(J) - mehrere Joins, aber nur eine Komposition - „Es kann mehrere gleiche Verbindungen geben, aber nur eine Bedeutung“ B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 30 3. relationales Datenbankmodell Operationen (5) Beispiel, Komposition von dem Join Äquivalenter SQL-Code: SELECT DISTINCT R.Start_Stadt, S.Ziel_Stadt FROM Verbindungen R, Verbindungen S WHERE R.Ziel_Stadt = S.Start_Stadt; B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 31 3. relationales Datenbankmodell Operationen (6) - Restriktion (Selektion) - Auswahl von Sätzen aus einer Relation, welche bestimmtes Prädikat erfüllen Äquivalenter SQL-Code: SELECT * FROM Verbindungen WHERE Start_Stadt = 'Leipzig'; Andere Operationen - Vereinigung Äquivalenter SQL-Code: SELECT R.Start_Stadt FROM Verbindungen UNION SELECT Stadt FROM Staedte; B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 32 3. relationales Datenbankmodell Andere Operationen (2) - Differenz Äquivalenter SQL-Code: SELECT S.Stadt FROM Staedte S UNION MINUS SELECT Start_Stadt FROM Verbindungen; - Durchschnitt Äquivalenter SQL-Code: SELECT S.Stadt FROM Verbindungen V, Staedte S WHERE V.Start_Stadt = S.Stadt; B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 33 3. relationales Datenbankmodell Redundanzen - jeder Fremdschlüssel ist eine Redundanz des Primärschlüssels - mehrmalige Speicherung der selben Information - Vorteil: Anfragen können leichter werden - Nachteil: Möglichkeit der Entstehung von Inkonsistenzen B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 34 3. relationales Datenbankmodell Inkonsistenz Name zu Personalnummer 6 ist nicht mehr eindeutig B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 35 3. relationales Datenbankmodell Codds (strenge) Regeln - 1986 Publikation 1986, Anforderungen an ein relationales Datenbank Management System (RDBMS) 0. Ein RDBMS muss die Datenbanken vollständig über seine relationalen Fähigkeiten verwalten. 1. Alle Informationen sind explizit als Werte in Tabellen darzustellen. 2. Zugriff auf jeden Wert durch Kombination von Tabellenname, Primärschlüssel und Spaltenname möglich. 3. Systematische Behandlung von Nullwerten 4. Struktur einer Datenbank ebenfalls in Tabellenform Zugriff darauf mit Abfragesprache 5. Abfragesprache mit Befehlssatz für Datendefinition, Manipulation, Integritätsregeln, Autorisierung und Transaktionen B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 36 3. relationales Datenbankmodell Codds (strenge) Regeln (2) 6. Aktualisieren von Sichten, auch durch das System möglich. 7. Abfragen und bearbeiten ganzer Tabellen (einfügen, aktualisieren, löschen) 8. Physikalische Datentunabhängigkeit, Zugriff unabhängig von den physikalischen Zugriffsmethoden oder den Speicherstrukturen der Daten beliebige Änderung der physikalischen Datenbankstruktur 9. Logische Datentunabhängigkeit, einerseits existieren die logischen Strukturen der Datenbank, andererseits sieht jeder Benutzer nur den für ihn relevanten Ausschnitt der gesamten logischen Struktur. (Benutzerrollen / Views) 10. Unabhängigkeit der Integrität, Definition von Integritätsregeln in Datenbanksprache, Speicherung im Systemkatalog, keine Umgehung möglich. 11. Verteilungsunabhängigkeit, logische Zugriff ändert sich bei Verteilung nicht. 12. Kein Unterlaufen der Abfragesprache (Low-Level-Sprachen) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 37 3. relationales Datenbankmodell Einschätzung - rein theoretischer Ansatz - dynamische Erweiterung der Informationswelt möglich - Teilsichten sind möglich (Modularisierung) - Komplexe Sachverhalte können dank algebraischer Gesetze optimiert werden - Änderung der Datenstruktur möglich, weil Zusammenhang der Informationen auf Logikebene B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 38 Gliederung 1. Einleitung 2. B-Bäume 3. relationales Datenbankmodell 4. Zusammenfassung B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 39 4. Zusammenfassung Zusammenfassung - B-Bäume relationales Datenbankmodell -1976/77 der Prototyp R (IBM) - erste kommerzielle DB, Oracle 1979 (Relational Software Inc.) - heute : DB2 (IBM), Ingres, Informix (IBM), Sysbase, SQL-Sever (MS) - geschätzter Marktwert des Datenbanksektor 30 Milliarden $ - sowie aufbauende Produkte: SAP… B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 40 4. Zusammenfassung Zusammenfassung (2) Gründe für den Erfolg - einfach formalisiertes Modell (Codd) - einfache Benutzerschnittstelle SQL (Chamberlin und Reisner) - Algebra als Basis für Codeoptimierung (Codd) - Abbildung der Information auf Relationen und diese auf auf B-Bäume - Möglichkeit der Mehrbenutzertransaktionen (Gray) - Robustheit durch Selbstbalancierung und Selbstorganisation der B-Bäume (Bayer) - gute Skalierbarkeit durch die log-Operationskosten der B-Bäume (Bayer) B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 41 Quellen Springer, Software Pioneers - Contributions of Software Engeenering, Manfred Broy & Ernst Denert Technische Universität München http://wwwbayer.in.tum.de/cgi-webcon/webcon/lehrstuhldb/details/Mitarbeiter/num/5/1 IBM http://www.research.ibm.com/resources/news/20030423_edgarpassaway.shtml Wikipedia, Die freie Enzyklopädie http://de.wikipedia.org/wiki software design & managment http://www.sdm.de/de/it-wissen/themen/sdmkonf-2001/index.html HTML-Version „SQL in 21 Tagen“ http://download.pearsoned.de/leseecke/SQL_21Tg/data/kap01.htm B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 42 Ende Danke B-Bäume & relationales Datenbankmodell von R.Bayer und E.F. Codd 43