Induktion_im_Generator
Werbung

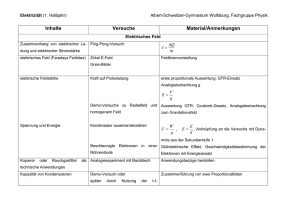
Induktion eines Sinus-förmigen Wechselstroms Inhalt • Faradaysches Induktionsgesetz • Induzierte elektrische Feldstärke bei Änderung des Winkel zwischen Fläche und Magnetfeld • Der sinusförmige Wechselstrom Das Faradaysche Induktionsgesetz „Bei Änderung des magnetischen Flusses wird eine elektrische Spannung induziert“ d d U A B dt dt B A U Induktion bei Änderung des Winkels, des Magnetfelds und der Fläche B A Induktion bei Änderung der Fläche, der Feldstärke oder des Winkels d U (t ) A B cos (t ) Induktionsgesetz dt Konstante Feldstärke, U (t ) A B cos konstanter Winkel U (t ) A B cos U (t ) A B (t ) sin (t ) U (t ) A B sin t Konstante Fläche, konstanter Winkel Konstante Fläche, konstante Feldstärke Im Falle konstanter Winkelgeschwindigkeit Induktion in einer Schleife Induzierte Spannung: 0 -1 1 d U dt U A B Fläche A Magnetische Feldstärke B Induktion bei Drehung der Fläche im konstanten Magnetfeld U (t ) A B (t ) sin (t ) (t ) t Konstantes Magnetfeld, konstanter Fläche Winkel bei konstanter Winkelgeschwindigkeit U (t ) A B sin t U (t ) U 0 sin t Induziert wird Sinusförmiger Wechselstrom Induktion in einer rotierenden Schleife 0 -1 Induzierte Spannung: U U 0 sin t 1 Fläche A Magnetische Feldstärke B Verlauf der Spannung bei Drehung mit konstanter Winkelgeschwindigkeit t U (t ) U 0 sin t T s • Versuch Induktion einer elektrischen Spannung Zusammenfassung • Drehen einer Leiterschleife im Magnetfeld ändert den Winkel zwischen magnetischer Feldstärke und Flächennormale • Durch Induktion entsteht ein Sinus-förmiger Wechselstrom • Die Sinus-Form ist besonders wertvoll: Induzierte Spannungen sind proportional zu deshalb kann Strom dieser Art für weitere Induktionsvorgänge eingesetzt werden I ,