Die Poissonverteilung

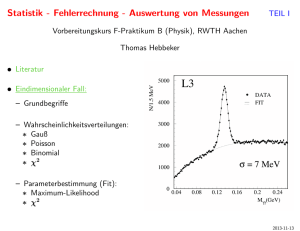
Die Poissonverteilung
Voraussetzung
• Die Beobachtungen seien Zahlen
voneinander unabhängiger ZufallsEreignisse, die in gleichen Zeitintervallen
eingetreten sind
• Die Verteilung dieser Zahlen wird durch
die Poisson-Verteilung beschrieben
Versuch
•
Beobachtung der Anzahl der Zerfallsereignisse
in Uranpechblende innerhalb von Intervallen zu
5 Sekunden
1. Zählrate etwa 250
2. Zählrate etwa 25
Anzahl der Beobachtungen pro Aufbau: 50
Die Poissonverteilung
f (k ) 

k
k!


e

Die Poissonverteilung
wird durch einen einzigen
Parameter beschrieben
Mittelwert
Standardabweichung
Näherung der Poisson- durch eine
Gaussverteilung

x  

2
1
f x  
e
2
2
Für mehr als 5 Freiheitsgrade kann die Poissondurch eine Gaußverteilung angenähert werden.
Diese Gaußverteilung wird durch einen einzigen
Parameter λ definiert:
 
 
Beispiel für die Näherung einer Poisson- (λ=5)
durch eine Gaussverteilung (μ=5, σ=√5)
PoisonVerteilung
Gaußkurve
Zusammenfassung
• Poisson-Verteilung, deren Objekte sind
natürliche Zahlen
• Jede Zahl ist die Anzahl der in einem
Zeitintervall beobachteten Ereignisse
• Voraussetzung:
• Alle Zeitintervalle sind gleich lang
• Die Ereignisse sind voneinander
unabhängig
Zusammenfassung
• Die Poisson-Verteilung wird durch einen
Parameter bestimmt:
• Dem Mittelwert
• Die Standardabweichung ist die Wurzel
aus dem Mittelwert