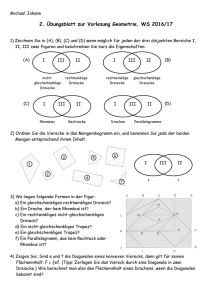
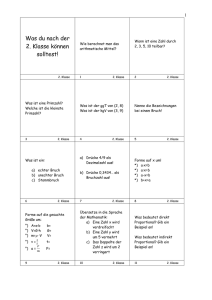
Übersicht: Dreiecke und Vierecke File

GEOMETRIE
Dreiecke und Vierecke
HOME
Dreiecke
Einteilung der Dreiecke nach Seiten:
(Allgemeines) Dreieck
Gleichschenkliges Dreieck
Gleichseitiges Dreieck
Einteilung der Dreiecke nach Winkel:
Spitzwinkliges Dreieck
Stumpfwinkliges Dreieck
Rechtwinkliges Dreieck
HOME
Das allgemeine Dreieck
C
b
ha
hc
A
Umfang:
u=a+b+c
a
hb
c
B
Flächeninhalt:
A=
A=
A=
a · ha
2
b · hb
2
c · hc
2
zurück zu den
Dreiecken
HOME
Das gleichschenklige
Dreieck
zurück zu den
Dreiecken
C
b
a
Flächeninhalt:
hc
A
A=
ha
hb
c
B
A=
Umfang:
u=a+b+c
A=
a · ha
2
b · hb
2
c · hc
2
HOME
Das gleichseitige Dreieck
C
a
a
ha
ha
Flächeninhalt:
ha
A=
A
a
B
a · ha
2
zurück zu den
Dreiecken
HOME
Das spitzwinklige Dreieck
C
b
ha
hc
A
Umfang:
u=a+b+c
a
hb
c
B
Flächeninhalt:
A=
A=
A=
a · ha
2
b · hb
2
c · hc
2
zurück zu den
Dreiecken
HOME
Das stumpfwinklige
Dreieck
C
zurück zu den
Dreiecken
hc
a
b
hb
B
c
A
ha
Umfang:
Flächeninhalt:
A=
A=
u=a+b+c
A=
a · ha
2
b · hb
2
c · hc
2
Die Höhe kann auch außerhalb des
Dreiecks liegen!
Siehe ha und hc!
Damit diese Höhen eingezeichnet
werden können, musst du die Seiten
des Dreiecks verlängern!
HOME
Das rechtwinklige Dreieck
C
b
a
hc
A
Umfang:
u=a+b+c
c
B
Flächeninhalt:
A=
A=
a·b
2
c · hc
2
zurück zu den
Dreiecken
HOME
Vierecke
Rechteck
Trapez
Deltoid
Parallelogramm
HOME
Das Rechteck
zurück zu den
Vierecken
Eigenschaften:
 Die Seiten a und b stehen im rechten Winkel aufeinander.
 Die gegenüberliegenden Seiten sind gleich lang.
 Die gegenüberliegenden Seiten sind parallel.
 Die beiden Diagonalen sind gleich lang.
 Die beiden Diagonalen halbieren sich.
 Die Diagonalen schneiden sich nicht im rechten Winkel.
Umfang:
Flächeninhalt:
u = a + b + a + b = 2a + 2b
A=a·b
HOME
Das Quadrat
zurück zu den
Vierecken
Eigenschaften:
 Die Seiten stehen im rechten Winkel aufeinander.
 Alle 4 Seiten sind gleich lang.
 Die gegenüberliegenden Seiten sind parallel.
 Die beiden Diagonalen halbieren sich.
 Die Diagonalen schneiden sich im rechten Winkel.
Umfang:
Flächeninhalt:
u=a+a+a+a=4·a
A=a·a
oder:
A
d d
2
HOME
Das Parallelogramm
zurück zu den
Vierecken
Eigenschaften:
 Die Seiten a und b stehen nicht im rechten Winkel zueinander.
 Je 2 Seiten sind gleich lang.
 Je 2 Seiten sind parallel.
 Die beiden Diagonalen halbieren sich.
 Die beiden Diagonalen sind nicht gleich lang.
 Die Diagonalen schneiden sich nicht im rechten Winkel.
Umfang:
Flächeninhalt:
u = a + b + a + b = 2a + 2b
a  ha b  hb
A

2
2
HOME
Die Raute
zurück zu den
Vierecken
Eigenschaften:
 Die Seiten a und b stehen nicht im rechten Winkel aufeinander.
 Alle 4 Seiten sind gleich lang.
 Je 2 Seiten sind parallel.
 Die beiden Diagonalen halbieren sich.
 Die beiden Diagonalen sind nicht gleich lang.
 Die Diagonalen schneiden sich im rechten Winkel.
Umfang:
Flächeninhalt:
u=a+a+a+a=4·a
A=a·h
oder:
e f
A
2
HOME
Das Trapez
zurück zu den
Vierecken
Eigenschaften:
 Es gibt nur ein Paar parallele Seiten.
 Die beiden Diagonalen halbieren sich nicht.
 Die beiden Diagonalen sind nicht gleich lang.
 Die Diagonalen schneiden sich nicht im rechten Winkel.
Umfang:
Flächeninhalt:
u=a+b+c+d
A
(a  c)  h
2
Eine Sonderform: Das Gleichschenkliges Trapez
HOME
Das gleichschenklige Trapez
zurück zu den
Vierecken
Eigenschaften:
 Es gibt nur ein Paar parallele Seiten.
 Die nicht-parallelen Seiten sind gleich lang.
 Die beiden Diagonalen halbieren sich.
 Die beiden Diagonalen sind gleich lang.
 Die Diagonalen schneiden sich nicht im rechten Winkel.
Umfang:
Flächeninhalt:
u = a + b + c + b = a + 2b + c
A
(a  c)  h
2
HOME
Das Deltoid
zurück zu den
Vierecken
Eigenschaften:
 Je 2 benachbarte Seiten sind gleich lang.
 Kein Seitenpaar ist parallel.
 Die beiden Diagonalen sind nicht gleich lang.
 Nur eine Diagonale halbiert die andere Diagonale.
 Die Diagonalen stehen im rechten Winkel aufeinander.
Umfang:
u = a + b + b + a = 2a + 2b
Flächeninhalt:
e f
A
2