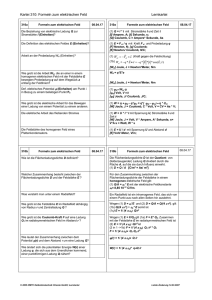
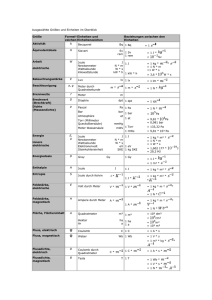
Arbeit bei „geschlossenem Weg“
Werbung

Arbeit, Energie Inhalt • Begriffe: Arbeit, Energie • Physikalische Vorgänge mit Bezug zu Energie • Der Energie-Erhaltungssatz • Energie Austausch zwischen Systemen • Energie im konservativen elektrischen und im Gravitationsfeld • Energie im Wirbelfeld Arbeit und Energie • Die Energie eines Systems ist ein Maß für die an ihm zu- bzw. abgeführten Arbeit • Äquivalente Begriffe des „täglichen Lebens“: – Energie verhält sich zu Arbeit wie Kontostand zu Kontobewegungen – Beachte: Stabile Währung, Kontostand immer > 0 Arbeit, Energie gibt es in Verbindung mit • • • • • • Kraft, Weg, Geschwindigkeit Transport elektrischer Ladung Feldstärken, d. h. zum Feld-Aufbau Elektromagnetischen Wellen Wärme Massen Der Energieerhaltungssatz • Die Gesamtenergie bleibt konstant, Energie kann aber ausgetauscht und umgewandelt werden • Systeme, in denen dieser Satz gilt, nennt man „abgeschlossen“ „Arbeit ist Kraft mal Weg“ SI-Einheit: 1 Nm=1 J (1 Joule) Arbeit ist Austausch von Energie Joule Dem System wird Arbeit zugeführt: Vorzeichen: Plus Joule Vom System wird Arbeit abgeführt: Vorzeichen: Minus -1 1 -1 1 „System 1“ „System 2“ Arbeit und Energie in Beziehung zu Kraft und Weg Definition der Arbeit Formel SI Einheit W F s 1 Nm=1 J Konstante Kraft in „1 Joule“ einem Intervall s W F (s ) ds s2 Anmerkung 1J Die Kraft sei Funktion des Weges s 1N Kraftvektor 1m Vektor eines WegIntervalls s1 F s Beispiel (1): Arbeit im Gravitationsfeld Joule 1 s h F m g W F s m g h Beispiel (2): Arbeit im elektrischen Feld F qE q s W F s q E s Arbeit bei unterschiedlicher Richtung von Kraft und Weg Beispiel (3): Arbeit im Gravitationsfeld Joule 1 h F s s W F s m g s cos F m g h Skalarprodukt zweier Vektoren am Beispiel der Arbeit W F s F s cos F s F 1J Arbeit 1N Kraft 1m Weg 1 rad F cos s Winkel zwischen beiden Vektoren Skalarprodukt zweier Vektoren • Das Ergebnis ist eine Zahl, ein „Skalar“ • „Produkt aus dem Betrag des ersten Vektors und dem Betrag der Projektion des zweiten auf den ersten“ oder: • „Produkt der Beträge beider Vektoren und dem Cosinus des Winkels zwischen ihnen“ Arbeit bei „Geschlossenen Wegen“ Das gesamte System bestehe aus zwei Teil-Systemen: 1. Kondensator mit positiver Ladung 2. Gewicht im Gravitationsfeld Arbeit im elektrischen Feld bei „geschlossenem Weg“ Q Joule -1 1 q W F s W F s W W 0 Keine Arbeit auf geschlossenen Wegen – in „konservativen“ Feldern • • • Auf dem Weg von + nach – wird aus dem System (1) Energie abgeführt und dem System (2) zugeführt, z.B. zum Heben des Gewichts Zur Rückführung von - nach + wird die Energie aus System (2) dem System (1) wieder zugeführt In Summe wurde keine Arbeit geleistet „Konservatives“ Feld Q Joule -1 q W F ds 0 1 „Konservatives“ Feld Q q W F ds 0 Beispiele zur Arbeit in elektrischen Feldern • 1.Bewegung einer Ladung in einem konservativen elektrischen Feld • 2. Bewegung einer Ladung in einem elektrischen Wirbel-Feld Arbeit bei „geschlossenem Weg“ Q W F ds 0 Felder mit dieser Eigenschaft bezeichnet man als „konservativ“ Nicht konservativ: Das elektrische Wirbelfeld Elektrische Feldstärke Geschlossener Weg W F ds E ( s )ds 0 Das Wirbelfeld entsteht um ein zeitlich veränderliches magnetisches Feld Magnetische Feldstärke Elektrische Feldstärke „Perpetuum Mobile“ im Wirbelfeld? • Ein elektrisches Wirbelfeld entsteht um ein zeitlich veränderliches magnetisches Feld • Die Energie wird von außen zum Feldaufbau zugeführt Potential, Spannung • In konservativen Feldern kann man jedem Punkt ein „Potential“ zuordnen: Quotient aus der Arbeit, die aufzubringen ist, um mit einem geeigneten Probekörper den Punkt zu erreichen, und der Ladung des Probekörpers • Eine Potentialdifferenz zwischen zwei unterschiedlichen Orten in einem elektrischen Feld nennt man „elektrische Spannung“