System 1
Werbung

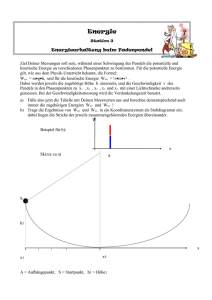
Arbeit, Energie Inhalt • • • • • • Begriffe: Arbeit, Energie Potentielle Energie Kinetische Energie Der Energie-Erhaltungssatz Energie Austausch zwischen Systemen Energie im konservativen Feld (Elektrisches Feld und Gravitationsfeld) • Energie im Wirbelfeld Arbeit und Energie • Die Energie eines Systems ist ein Maß für die an ihm zu- bzw. abgeführten Arbeit • Äquivalente Begriffe des „täglichen Lebens“: – Energie verhält sich zu Arbeit wie Kontostand zu Kontobewegungen – Beachte: Stabile Währung – Kontostand immer > 0 Arbeit ist Austausch von Energie Dem System wird Energie zugeführt: Vorzeichen: Plus Joule -1 1 „System 1“ Vom System wird Energie abgeführt: Vorzeichen: Minus Joule -1 1 „System 2“ Der Energieerhaltungssatz • Die Gesamtenergie bleibt konstant, Energie kann aber ausgetauscht und umgewandelt werden • Systeme, in denen dieser Satz gilt, nennt man „abgeschlossen“ „Arbeit ist Kraft mal Weg“ SI-Einheit: 1 Nm=1 J (1 Joule) Definition der mechanischen Arbeit SI Einheit W F s F s Anmerkung 1 Nm=1 J Konstante Kraft in „1 Joule“ einem Intervall Δs 1N Kraftvektor 1m Vektor eines WegIntervalls Arbeit mit Kraft als Funktion des Orts SI Einheit W F (s ) ds s2 s1 F (s ) Anmerkung 1 Nm=1 J Die Kraft sei Funktion „1 Joule“ des Orts s 1N Kraftvektor, Funktion des Orts s Arbeit im Gravitationsfeld Joule 1 s h F m g W F s m g h Die potentielle Energie W pot m g h Joule 1 h •Das angehobene Gewicht zeigt die „potentielle Energie“ Wpot •Die potentielle Energie befähigt das System, zu irgendeinem Zeitpunkt Arbeit abzugeben Austausch potentieller Energie zwischen zwei Systemen Joule Joule -1 1 -1 1 „System 1“ „System 2“ Die kinetische Energie s System 1: Träge Masse m Zeit t, Geschwindigkeit v System 2 mit potentieller Energie Wpot Die potentielle Energie Wpot dient in diesem Vorgang zur konstanten Beschleunigung der Masse m Kinetische Energie bei konstanter Beschleunigung Formel SI Anmerkung W F s 1J Konstante Kraft F im Intervall Δs F m a 1N Kraft auf Masse m 1m In der Zeit t durchfahrener Weg 1 2 s at 2 v a t 1 v W m a a 2 a 1 m/s 2 1J Nach der Zeit t erreichte Geschwindigkeit F und Δs eingesetzt, t durch v formuliert Definition der kinetischen Energie Formel Wkin 1 2 mv 2 SI 1J Anmerkung Kinetische Energie Eine sich mit Geschwindigkeit v bewegende Masse trägt die kinetische Energie Wkin=mv2/2 , unabhängig von der Art der Beschleunigung Vollständige Umwandlungsfolge bei diesem Vorgang s Umwandlungsfolge: Potentielle Energie Kinetische Energie Kinetische + Rotations-Energie Wärme-Energie Beispiel für die Umwandlung von potentieller in kinetische Energie Formel W pot Wkin 1 2 mv 2 Wkin W pot SI Anmerkung 1J Potentielle Energie des Antriebs 1J Kinetische Energie 1J Die potentielle Energie zu Beginn ist gleich der kinetischen Energie am Ende Die potentielle und kinetische Energie beim Fall W pot m g h Joule 1 h 1 2 Wkin m v 2 Berechnung der Fallgeschwindigkeit aus dem Energie-Erhaltungssatz Formel W pot m g h 1 2 Wkin m v 2 1 2 m g h mv 2 v 2g h SI Anmerkung 1J Potentielle Energie vor dem Fall 1J Kinetische Energie nach Fall durch die Strecke h 1J Energie-Erhaltung Geschwindigkeit nach 1 m/s dem Fall aus der Höhe h Arbeit im elektrischen Feld F qE q s W F s q E s Arbeit auf „geschlossenen Wegen“ Das System bestehe aus zwei Komponenten: – Kondensator mit positiver Ladung – Gewicht im Gravitationsfeld Arbeit im elektrischen Feld auf einem „geschlossenen Weg“ Q Joule -1 1 q Am Kondensator verrichtete Arbeit: W F s E q s W E ( s ) qds W W 0 „Konservative“ Felder • • Ein Feld, in dem auf geschlossenen Wegen die Summe der Arbeiten Null ist, wird als „konservatives Feld“ bezeichnet In konservativen Feldern ist die Arbeit zwischen zwei Punkten vom Weg unabhängig W F ds 0 Potential, Spannung • In konservativen Feldern kann man jedem Punkt ein „Potential“ zuordnen: Quotient aus – der Arbeit, die aufzubringen ist, um mit einem geeigneten Probekörper den Punkt zu erreichen, – und der Ladung des Probekörpers • Eine Potentialdifferenz zwischen zwei unterschiedlichen Orten in einem elektrischen Feld nennt man „elektrische Spannung“ Potentiale im elektrischen Feld (r2 ) (r4 ) Q (r1 ) Platte auf „Erdpotential“ (r3 ) Elektrisches Potential eines Punktes Einheit W (r ) (r ) q Anmerkung Das Potential ist ein Quotient, Zähler: Arbeit, um eine Ladung 1 J/C=1 V von einem vereinbarten Ort an „ 1 Volt“ diesen Punkt zu verschieben, Nenner: Betrag der Ladung Die elektrische Spannung Einheit W U q Anmerkung Die elektrische Spannung zwischen zwei Punkten ist ein 1 J/C=1 V Quotient, Zähler: Arbeit, um eine Ladung „1 Volt“ von einem zum anderen Punkt zu verschieben, Nenner: Betrag der Ladung Die elektrische Spannung ist eine Potentialdifferenz Einheit U (r2 ) (r1 ) Anmerkung Die elektrische Spannung 1 J/C=1 V zwischen zwei Punkten „1 Volt“ ist die Differenz der Potentiale dieser Punkte Potentiale im elektrischen Feld (r2 ) Ladung q 1 0 (r4 ) Q 0,5 (r1 ) (r3 ) Arbeit W Ladung q Spannung U=W/q [V] Die elektrische Feldstärke bringt einige Punkte im Raum auf unterschiedliches Potential: Zwischen ihnen erscheint eine Spannung Bewegung einer Ladung in einem nicht konservativen elektrischen Feld Elektrische Feldstärke Geschlossener Weg W F ds E ( s ) qds 0 „Perpetuum Mobile“ im Wirbelfeld? • Ein elektrisches Wirbelfeld entsteht um ein zeitlich veränderliches magnetisches Feld • Die Energie wird von außen zum Feldaufbau zugeführt Das Wirbelfeld entsteht um ein zeitlich veränderliches magnetisches Feld Magnetische Feldstärke Elektrische Feldstärke Zusammenfassung • Arbeit ist Kraft mal Weg • Arbeit ist der Austausch von Energie zwischen zwei Systemen • In abgeschlossen Systemen gilt der EnergieErhaltungssatz • Bezüglich der Arbeit auf geschlossenen Wegen unterscheidet man: – Konservative Felder: Auf geschlossenen Wegen addieren sich geleistete und gewonnene Arbeiten zu Null – Wirbelfeder: Auf diesen Wegen wird bei jedem Umlauf Energie gewonnen oder zugeführt • In konservativen Feldern ist die Arbeit zwischen zwei Punkten im Raum vom Weg unabhängig: Jedem Punkt kann sein „Potential“ zugeordnet werden Potentiale im elektrischen Feld (r2 ) Finis (r4 ) Q (r1 ) Platte auf „Erdpotential“ (r3 )