m 1 + m 2

Physik für Studierende
der Fakultät III:
Punktmechanik
Vorlesung SS 2006
Prof. Adalbert Ding
Physikalische Grundgrößen
bestehend aus
Zahlenwert und Einheit
Größe
Einheit
Abk.
•
•
•
•
•
•
Meter
Sekunde
Coulomb
Kilogramm
Kelvin
Mol
[m]
[s]
[C]
[kg]
[K])
[1] )
Ort
Zeit
Ladung
Masse
(Temperatur
(Stoffmenge
Abgeleitete Größen (differentiell)




s
s
ds
 Geschwindi gkeit v  

t
t
dt



2
 v
v
dv d s
 Beschleuni gung a  


t
t
dt dt 2


 Impuls
p  mv


 p
p
dp
 Kraft
F 

t
t
dt
  
 Drehimpuls
l v p
  
 Drehmoment
M  r F
Dies sind Vektorgrößen, die orts- und zeitabhängig sein können
Vektoren (1)
Vektoren beschreiben gerichtete
Größen. Sie können durch Länge
(Größe) und Richtung oder durch
Komponenten beschrieben werden
•Dreidimensionaler (3D) Vektor (Normalfall)
3 Komponten (z.B. x, y, z) oder
1 Länge, 2 Winkel
•Zweidimensionaler (2D) Vektor (ebenes Problem)
2 Komponten (z.B.x,y) oder
1 Länge [r], 1 Winkel[φ]
•Mehrdimensionaler Vektor
n Komponten (z.B.x1,..xi,..xn)
Vektoren (2)
• Haben 2 Multiplikationsarten:
Inneres Produkt: Ergebnis skalar
Vektorprodukt: Ergebnis vektoriell
• Keine Division!
• Sonderfall: komplexe Zahlen definiert durch 2
Komponenten, bzw. Länge und Winkel
Produkt: Ergebnis komplex (nicht skalar)
Division: Ergebnis komplex (nicht skalar)
Vektorfelder
Die ortsabhängigen Vektoren werden in
Vektorfeldern zusammengefasst:
Beispiele:
Geschwindigkeitsfelder (z.B. Wetter, Meeresströmung)
Wärmeströmung
Elektrische und magnetische Felder
Beispiele
für
Vektorfelder:
Meeresströmung
im Schwarzen
Meer
Beispiele
für
Vektorfelder:
Ostsee
Erhaltungssätze
(nichtrelativistisch)
•
•
•
•
•
Ladung
Masse
Energie
Impuls
Drehimpuls
Der Impuls
• Die Größe der Bewegung ist durch
die Geschwindigkeit v und
die Masse m (Menge der Materie)
bestimmt:
p = m·v
• Sie wird Impuls genannt.
• Der Impuls ist eine Vektorgröße, ist also
gerichtet.
• Der Impuls kann nur durch das Einwirken einer
Kraft geändert werden
(s. 1. bzw. 2. Newtonsches Axiom).
Einzel- und Gesamtimpuls
m2
m1
V1
p1
P = p1 + p2 = m1V1+ m2V2
V: Geschwindigkeit im Laborsystem
V2
p2
Erstes Newtonsches Axiom
• Jeder Körper beharrt im Zustand der Ruhe
oder der gleichförmigen Bewegung, wenn
er nicht durch einwirkende Kräfte Fi
gezwungen wird, seinen Zustand zu ändern,
d.h. bei abwesenden Kräften bleibt der
Impuls konstant:
p = const. wenn Fi = 0
Zweites Newtonsches Axiom
• Die Änderung des Impulses ist der
Einwirkung der bewegenden Kraft
proportional und wirkt in die Richtung
der einwirkenden Kraft:
F = dp/dt =m·dv/dt + v·dm/dt
• Sonderfall m = const.:
F = m·dv/dt = m·a
NB:
Das 1. Newtonsche Axiom ist ein Sonderfall
des 2. Newtonsche Axioms für F=0
Drittes Newtonsches Axiom
• Die Wirkung ist stets der Gegenwirkung
gleich
oder
• Die Wirkung zweier Körper aufeinander ist
stets gleich und von entgegengesetzter
Richtung
Lineare Superposition
von Kräften
• Kräfte werden vektoriell überlagert
• Die meisten physikalischen Größen können
linear (skalar oder vektoriell) überlagert
werden
• Da die Vektoren ortsabhängig sind
entstehen ortsabhängige Vektorfelder
Überlagerung von Kräften
An der Masse greifen 6 Kräfte an (Pfeile zeigen die
Richtung an). Wie groß ist die resultierende Kraft?
5N
6N
4N
60° 60°
60°
60°
60° 2N
4N
3N
Wie groß ist die resultierende
Kraft? Geben Sie diese
graphisch und numerisch an!
Welche Kraft muss addiert
werden, damit die Masse in
Ruhe (d.h. kraftfrei) bleibt.
Überlagerung von Kräften (2)
An der Masse greifen 5 Kräfte an (Pfeile zeigen die
Richtung an). Wie groß ist die resultierende Kraft?
11N
4N
90°
45°
6N
45°
45°
4N
3N
Wie groß ist die resultierende
Kraft? Geben Sie diese
graphisch und numerisch an!
Welche Kraft muss addiert
werden, damit die Masse in
Ruhe (d.h. kraftfrei) bleibt.
Grundlegende Kräfte
• Gravitationskraft
• Elektrostatische Kraft
• Magnetische (Lorenz-)Kraft
• 2 Kernkräfte
Gravitationsgesetz

m1  m2  0
F12  G 
 r12
2
r12
r12: Abstand der Massenmittelpunkte,
r120 gibt die Richtung an (Länge = 1)
G: Gravitationskonstante G = 6,67·10-11 Nm2kg-2
Für einen kleinen Körper auf der Erdoberfläche ist
r12 = rE Erdradius, m2 = mE Erdmasse, m1 Probemasse:
F = m(1)·g;
g: Erdbeschleunigung=9,81 m·s-
Große Physiker und Astronomen vor 1700 °
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Thales v. Milet (624 - 547 v.u.Z.)
Pythagoras
(580 - 496 v.u.Z)
Demokrit
(ca. 420 v.u.Z.)
Archimedes
(287 - 212 v.u.Z.)
Erathosthenes (276 - 195 v.u.Z.)
Hipparch
(190 - 125 v.u.Z.)
Ibn Junus
(ca. 1000)
Leonardo da Vinci
(1452 – 1519)
Gallileo Gallilei
(1564 – 1642)
Nikolaus Kopernikus
(1473 – 1543)
Johannes Kepler
(1571 – 1630)
Rene Descartes
(1596 – 1650)
Pierre Fermat
(1601 – 1665)
Otto v. Guericke
(1602 – 1686)
Christian Huygens
(1629 – 1695)
Isaac Newton
(1643 – 1727)
E. Torricelli
(1608 – 1647)
Blaise Pascal
(1623 – 1662)
Robert Boyle
(1627 – 1691)
E. Maylotte
(1620 – 1684)
Experimentelle Bestimmung der
Gravitationskonstante G °
G: Gravitationskonstante G = 6,67·10-11 Nm2kg-2
Kräfte (abgeleitete)
•
•
•
•
Reibungskräfte
Fliehkräfte
Corioliskraft °
Atomare und molekulare Kräfte °
z.B. zwischen Teilchen im Atom,
zwischen Atomen,
aber auch in Flüssigkeiten und Festkörpern
Spezifische Größen:
Druck p
Druck:
Kraft pro Fläche
p = Fn/A
Kinetische Energie
• ist mechanische Bewegungsenergie
Ekin =m/2 v2
• Energiesatz gilt
Erhaltungssätze
(nichtrelativistisch)
•
•
•
•
•
Ladung
Masse
Energie
Impuls
Drehimpuls
Energie, Arbeit, Leistung
•
•
•
•
Mechanische (kinetische) Energie: m/2·v2
Mechanische Arbeit W = F·s   F·ds
Leistung N= W/t
Wenn die Arbeit, einen Gegenstand von Punkt nach
Punkt B zu bringen, unabhängig ist vom Weg, kann die
Kraft F als 3D-Ableitung (Gradient, Steigung) eines
Potentials V geschrieben werden:
• F = -grad V (-dV/dx, -dV/dy, -dV/dz)
• Solche Kräfte werden konservativ genannt
• Die Gravitationskraft, die Coulombkraft sind konservative Kräfte, die Reibungskräfte, die Corioliskraft sind
nicht konservativ.
Erhaltung der mechanischen Energie
Egesamt = Epot + Ekin + Erot
+ Etherm + Ephoton
+ Eelstat + Emagn + ( Egrav )
Bei Abwesenheit anderer Energieformen
(Thermische Energie, Photonen, Feldenergien) gilt
Egesamt = Epot + Ekin + Erot
Erhaltung der mechanischen Energie
Beginn:
Ekin=0, Erot =0
Egesamt = Epot (1)
Ende:
Egesamt = Epot(2) + Ekin + Erot
V12 = Epot(2) - Epot (1) = Ekin + Erot
Freier Fall
Die Energie eines im Erdfeld fallenden Körpers ist
F· h = m·g·h
Nach Durchfallen der Höhe h ist die kinetische Energie
m 2
·v  m·g·h
2
oder
v 2  2·m·g·h
v  2mgh
Die
Vakuumkanone(2)
Ein Tennisball
mit Leitwerk wird in ein evakuiertes Rohr
(blau) hineingesaugt und durchläuft dort die Strecke
l=1m. Der Außendruck beträgt 1000 hPa.
Wie groß ist die kinetische Energie Ekin und die
Geschwindigkeit v nach Durchlaufen dieser Strecke?
Lösung:
l
F=A·p
• Arbeit = kinetische Energie = F·l
• Beispiel
Tennisball: 68g Durchmesser: 6,6 cm
m=0,08kg (inklusive Leitwerk);
A =34,2 cm2 =34,2·10-3m2
p 105 Pa (1000 hPa)
Ekin = 34,2 ·10-4m2·105 ·Nm-2 · 1m = 342 J
• Ekin = m/2·v2  v = (2E/m)0,5 =85530,5
 92,5 m ·s-1 {332 km/h}
Schwerpunkt
• Der Schwerpunkt eines Körpers ist ein ideeller Punkt,
in dem man sich die gesamte Masse des Körpers oder
der Körper (z.B. Punktmassen) vereinigt denken kann.
• Im Schwerefeld kann der Körper durch eine Gegenkraft, die auf den Schwerpunkt wirkt und gleich aber
entgegengesetzt der Kraft ist, die auf die Gesamtmasse wirkt, im Gleichgewicht gehalten werden
• Der Schwerpunkt kann auch außerhalb des oder der
Körper liegen
Schwerpunktgeschwindigkeit
P = p1 + p2 = m1V1+ m2V2
P = M·vs = (m1+ m2)Vs
Vi: Geschwindigkeit im Laborsystem
vi: Geschwindigkeit im Schwerpunktsystem
vs: Geschwindigkeit des Schwerpunkts
Schwerpunkt
V1
r2
m1
r1
p1
vs
v1
rs
z
y
x
V2
v2
vs
R2
R1
m2
p2


 m1R1  m 2 R 2
rs 
m1  m 2
  
r1  R1  rs
 

r2  R 2  rs
Schwerpunkt von 2 Punktmassen
m2
R2
r2
Schwerpunkt
Ri: Koordinaten im Laborsystem
rs
r1
z


 m1R1  m 2 R 2
rs 
m1  m 2
  
r1  R1  rs
 

r2  R 2  rs
ri: Koordinaten im Schwerpunktsystem
y
R1
x
m1
rs: Koordinate des Schwerpunkts
mi: Punktmassen
Schwerpunkt
von mehreren Punktmassen
m2
m5
r2
m4
r5
r4
Schwerpunkt
R4
R2
R5
rs
r3
m3
z
m1
y
x
R1
r1
R3

n

mi R i
rs  
mi
i 1
  
ri  R i  rs
Einfaches Tragwerk
Fdübel = Fhor
Regal (2D)
Zug
Dübel
Fhor
y=1m
Druck
x=2m
Wand
Fdiag
Last
FL
Beispiel: gegeben m=10 kg, y=1m, x=2m
gesucht: FL, Fhor, Fdiag (Druck oder Zugkräfte?)
Lösung: FL=100N, Fhor=(x/y)·FL=200N;
Fdiag=(FL2+Fhor2)0,5 =224N
Einfaches Tragwerk (2)
Unsymmetrische Schaukel (2D)
Flx
Frx
Fly
FG
Fry
Flx + Frx = 0
Fly + Fry + FG = 0
Fly
Newton I
Gegeben: m, h, xl, xr
Gesucht: FG, Fl, Fr (in Komponenten)
und Vektordarstellung
h
Last
FG = m·g
xl
xr
Fundament
Drehgrößen
Neue Größen:
Winkelgeschwindigkeit  = dφ/dt
Winkelbeschleunigung  = d/dt
• Drehimpuls
:l =rxp
• Drehmoment
:M =rxF
• Rotationsenergie : Erot = p2/2m = I/2 ·
2
Drehimpuls- und Drehmomentvektoren
zeigen in Richtung Drehachse !
Erhaltungssätze
(im geschlossenen System, nichtrelativistisch)
Ladung
Masse
Energie
Impuls
Drehimpuls
Drehgrößen vs. Lineare Größen
Drehgrößen
Lineare Größen
• Drehimpuls
• Drehmoment
• Rotationsenergie
• Impuls
• Kraft
• Kinetische Energie
Gegenüberstellung von
linearen Größen und Drehgrößen
(1)
•
•
•
•
•
•
Strecke s
Geschwindigkeit v
Beschleunigung a
Masse m
Kraft F
Impuls p






Drehwinkel 
Winkelgeschwindigkeit 
Winkelbeschleunigung 
Trägheitsmoment J
Drehmoment M
Drehimpuls l
Man beachte die unterschiedlichen Dimensionen
auf der linken und der rechten Seite
Gegenüberstellung von
linearen Größen und Drehgrößen°
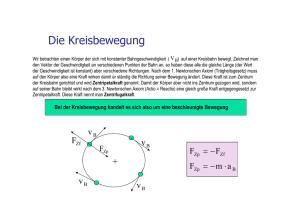
Zentrifugalbeschleunigung
v1


|v1| = |v2| = v
v·sin() v·
v0
b ra d
v·cos()  v·1 = v
t
2
v v1 - v 0

d
v


v
v
 v   r  2 
t
t
t
dt
r
da
sonst ist
v  r 


 
b ra d    (  r )


wenn r senkrecht auf 
Zentrifugalkraft
r
v1

t
Frad  m  b rad
da

v0
2
d
v
 mv
 mv    mr   2  m
dt
r
v  r 
Karussel
r
Fzent  mr  2
Fg  mg θ
Fres  (mg ) 2  (mr 2 ) 2
 r 

 mg 1  
 g 
2
2
Fzent r 2
tan  

Fg
g
Beispiel: m=50 kg, r = 10 m, =2πf = 1 s-1 (1 Umdrehung in ca.6 s)
gesucht: Fg , Fzent , Fres , θ
Fres  700 N ; θ = 45° (θ unabhängig von der Masse)
Corioliskraft °
Verschiedene Koordinatensysteme, die sich gegenseitig linear
bewegen, haben dieselben Naturgesetze (Inertialsysteme).
Rotieren sie gegeneinander, so treten zusätzliche (Pseudo-)Kräfte auf:
1. Die Zentrifugalbeschleunigung (s.o)
2. Corioliskräfte
Gleichförm ige relative Translatio nsbewegung :

 
 
V  V - v
a  a
Gleichförm ige relative Rotationsb ewegung :

  
    
 
V  V -   r
a   a -   (  r ) - 2    V
Corioliskraft (1) °
Das Foucaultsche Pendel: Ein auf der Erde in x-y-Richtung beweg 
liches Pendel erfährt eine Coriolis-Beschleunigung 2   V , die
senkrecht zur Pendelbewegung wirkt. Dadurch wird die Ebene, in
der das Pendel schwingt, gedreht (an den Polen: 360°/d).
Corioliskraft (2) °
Wettersystem:
rechts: Nordhalbkugel
unten: Südhalbkugel
Corioliskraft (3): Tornado °
Anwendung Newtonsche Axiome:
Statik
• Keine beschleunigte Bewegung, wenn die
Summe aller an einem Punkt angreifenden
Kräfte gleich Null wird:

 Fi  0
• Keine beschleunigte Drehung, wenn die
Summe aller Momente verschwindet:

 Mi  0
Einfaches Tragwerk
(alternative Berechnungsmethode)
Fdübel
Anwendung von Momenten:
ML+ MD= 0
y=1m
Dübel
Zug
Regal (2D)
MD=y·Fdübel
ML=x·FL
Drehpunkt
Wand
Druck
x=2m
Last FL
Beispiel: gegeben m=10 kg, y=1m, x=2m
gesucht: FL, ML,, MD, Fdübel (Druck oder Zugkraft?)
Beispiel: m=10 kgFL=100NML=200Nm
Fdübel= MD/y = -ML/y = -200N
Belasteter Balken (2D)
sS
s1
x
m1
s3
s2
y
Schwerpunkt
des Balkens
m2
m3
w
Lager
Lager
FL1
FLS
FL2
FLager
Beispiel: gegeben x=2m, y=3m, w=10m, m1=100kg, m2=200kg,
m3=0 (gewichtsloser Balken) oder m3= 50kg (Gewicht des Balkens)
gesucht: FL1, FL2, FLS, FLager (linkes und rechtes Lager; Kraftrichtung?)
und die entsprechenden Drehmomente
Anleitung: der Drehpunkt wird in das linke oder das rechte Lager gelegt!
Belasteter Balken (Fortsetzung)
Aufgabe:
gegeben x=2m, y=3m, w=10m, m1=100kg, m2=200kg,
m3=0
(gewichtsloser Balken) oder 50kg (Gewicht des Balkens)
gesucht: FL1, FL2, FL3, FLager (linkes und rechtes Lager; Kraftrichtung?)
und die entsprechenden Drehmomente
Anleitung: der Drehpunkt wird in das linke oder rechte Lager gelegt!
Lösung:
Gewichtsloser Balken: FL1=1000N, FL2=2000N, FLS=0,
s1=2m, s2=7m, sS=5m, s3=10m, M1=200Nm, M2=1400Nm, M3=10*Flager
- >M1+M2+M3=0
-> M3=-16000Nm, FLager =-1600N
Balken mit Gewicht: FL1=1000N, FL2=2000N, FLS=500N,
s1=2m, s2=7m, sS=5m, s3=10m, M1=2000Nm, M2=14000Nm,
M1S=250Nm, M3=100* Flager
-> M1+M2 +MS +M3 =0
-> M3=-16250Nm, FLager =-1625N
Komplexes Tragwerk °
Fachwerkbrücke
Modell einer Fachwerkbrücke mit 2 Lagern und 5 Knoten belastet durch 2 x 50
Krafteinheiten (Pfeile nach unten). Berechnet werden die Druckspannungen (blau)
und die Zugspannungen (rot) sowie die auf die Lager wirkende Kraft (Pfeil nach
oben). In allen Knoten muss die Summe der Kräfte gleich Null sein. Zusätzlich muss
die Summe der externen Kräfte (Pfeile) verschwinden.
Erhaltungssätze
(nichtrelativistisch)
•
•
•
•
•
Ladung
Masse
Energie
Impuls
Drehimpuls
Energiearten
•
•
•
•
•
•
•
Kinetische Energie
Potentielle Energie
Thermische Energie
Elektrostatische Energie
Magnetostatische Energie
Elektromagnetische Energie (z.B. Licht)
Kernenergie
Beispiel Energiespeicher
Mechanischer Energieinhalt eines Wasserbeckens:
Epot=Fs·h=m ·g ·h
m: Masse, h:Höhe, g:Erdbeschleunigung
Beispiel:
• Becken (50m·20m·2m=2000t), Höhe 20m
• 2·106kg ·10ms-2 ·10m=2·108 kgm2s-2 (Nm=J)
55kWh
Keplersche Gesetze
Keplersche Gesetze (1)
• Die Planeten laufen auf Elipsenbahnen, in
deren (einem) Brennpunkt die Sonne steht.
• Das Produkt aus Bahnradius und Geschwindigkeit ist konstant (Erhaltung des Drehimpulses)
• Das Quadrat der Umlaufzeit ist proportional
zur 3. Potenz des Bahnradius
Keplersche Gesetze (1a)°
Wie ist die Umlaufzeit definiert?
Ein (siderischer) Umlauf eines Himmelskörpers entspricht einem Bahnwinkel von 360° (in Richtung auf
weit entfernte Sterne und nicht auf
die Sonne).
Beispiel:
Mond
(Zentralgestirn
Sonne). Die scheinbare Umlaufzeit
(gleiche Richtung (Sternbild) am
nächtlichen Himmel) ist mit 27,32 d
2,2 d kürzer als die Zeit (29,5 d)
zwischen Neumond und Neumond
(gleiche Richtung zur Sonne)
Keplersche Gesetze (2)
Drehimpuls : l  p  r  m  v  r
Zentrifuga lkraft  Anziehungs kraft
m Planet  m Sonne
2
m Planet  r    G 
r2
 2  G  m Sonne
   
3
T
r
 
2
2
Beispiele zu den Keplerschen Gesetzen
• Die Keplerschen Gesetze gelten nicht nur für die
Bewegung der Planeten um die Sonne, sondern
auch für die Bewegung der Monde und Satelliten
um die Planeten
• Beipiel Erde:
Mond:
Bahnradius: rMond  3,84·105 km
Umlaufzeit: TMond  27,32 d
Frage:
Wie gross ist der Bahnradius, wenn die
Umlaufzeit TSat = 1d beträgt
(geostationäre Satelliten)?
rSat
 TSat
 
 TMond
2
3

  rMond  4  10 4 km

Beispiele zu den Keplerschen Gesetzen (2) °
(genauere Berechnung: siderale Umlaufzeiten und Berücksichtigung
des Schwerpunkts zwischen Erde und Mond)
• Beipiel geostationärer Satellit :
Mond: Bahnradius: rM-E  3,84402·105 km
siderale Umlaufzeit: TMond  27,32 d
Abstand vom Schwerpunkt: r
M-S
m Erde

 rM-E  0,98785  rM-E
m Mond m Erde
Frage: Wie gross ist der Bahnradius, wenn die siderale
Umlaufzeit
TSatellit  1 d sideral  1 d 
364,25
 0,99726 d
365,25
beträgt?
2
3
 TS a t 
  rMo n d  41785 km
rS a t  
 TMo n d 
Die Bahnradien werden vom Mittelpunkt der Massen gemessen!
Bahn- und Eigendrehimpulse der Himmelskörper °
Die Bahn- (
) und Eigendrehimpulsvektoren (
) von Sonne,
Planeten, Monden und Planeten- bzw. Mondbahnen, zeigen ebenso wie
der Drehimpuls der Sonnenbahn um die Zentralgalaxie in etwa
dieselbe Richtung:
Schiefe Ebene ohne Reibung
• Gegeben:
Masse des Körpers m=1,3 kg
Neigungswinkel α = 30°
Länge der schiefen Ebene l=5 m
m
FN α
FHA
• Wie groß ist die Gewichtskraft FG, die
Normalkraft FN und die Hangabtriebkraft
FHA?
• Wie groß ist die Geschwindigkeit v und die
Energie Ekin des Körpers am Ende der
schiefen Ebene?
• Wie groß ist h?
• Was bewirkt FHA?
• Welche Rolle spielt FN?
α
FG
h
α
Reibung
Reibungskraft FR
• Die Reibungskraft eines festen Körpers auf einer
festen Unterlage hängt nur von der senkrecht auf
die Unterlage wirkenden Kraft, der sog. Normalkraft FN ab, nicht jedoch von der Kontaktfläche.
Der Proportionalitätsfaktor wird mit μ bezeichnet.
• Die Richtung der Reibungskraft ist immer
entgegengesetzt der Bewegungsrichtung.
• Im Gegensatz dazu hängen die Reibungskräfte
von festen Körpern, die sich in einer Flüssigkeit
bzw. einem Gas bewegen von der Geschwindigkeit und der Form des Körpers ab.
Reibung
Reibungskraft FR
• Fester Körper auf Unterlage: FR=μ · FN
• Bewegung in einer viskosen Flüssigkeit:
FR=cv·v = 6πηrv für eine Kugel
v Geschwindigkeit
η dynamische Viskosität,
r Kugelradius
• Schnelle Bewegung in einem Gas.
FR=cw·ρ/2 · v2
cw Widerstandsbeiwert (formabhängig),
ρ Dichte
Reibungskraft FR
• Fester Körper auf Unterlage: FR=μ · FN
FR
Schiefe Ebene
α
FR ~FHA ~FLast =FN
FHA
FLast
α
Reibungskraft FR
• Fester Körper auf Unterlage: FR=μ · FN
FR
FR
FHA
α
FHA
α
FLast
α
FLast
Schiefe Ebene
FR ~FHA ~FLast =FN
Reibung fester Körper
Reibungskraft FR, Normalkraft: FN,
• Fester Körper auf Unterlage: FR=μ · FN
μ: Reibungskoeffizient
• Die Reibung ist vor Beginn der Bewegung
am größten (Haftreibung; μH),
• Gleitet der Körper auf der Unterlage so
verringert sich der Reibungskoeffizient
(Gleitreibung; μG)
• Rollt der Körper so ist die Reibung am
geringsten (Rollreibung; μR)
Reibung fester Körper °
Reibungskraft FR, Normalkraft: FN,
Reibungskoeffzient
Haftreibung µ0
Gleitreibung µ
•
•
•
•
•
•
•
•
0,95
0,5
0,6
0,015
0,15
0,04
0,4
0,04...0,2
0,8
0,25
0,5
0,01
0,1
0,04
0,3
0,04...0,2
Autoreifen auf Asphalt
Holz auf Holz
Stein auf Stein
Stahl auf Eis
Stahl auf Stahl
Stahl auf Teflon
Leder auf Metal
Ski auf Schnee
Reibung fester Körper: Beispiel Stein auf Stein,
• Übungsaufgabe: gegeben m1,m2, μ,
μ =0,4 (Stein auf Stein)
gesucht:FG, FS, FN, FR, a(m1)
Reibungskraft FR=μ ·FN,
Normalkraft: FN=g ·m
Im Gleichgewicht ist 2FS=FG und
FG=10·100 =1000 N
FS=500 N
FN= 10·60=600 N
FR=0,4 ·300 = 240 N
Resultierende Kraft: Fres= FS- FR
=500 – 240
=260 N
Die Beschleunigung der Masse m1 ist
m1 ·a(m1)=260N a(m1)=260N/60kg=4,33m·s-2
FS
FN
Rollen,
Ohne
Reibung
FS
FR
m1=60kg
FS
FS
FG
m2 =
100kg