Die Kreisbewegung

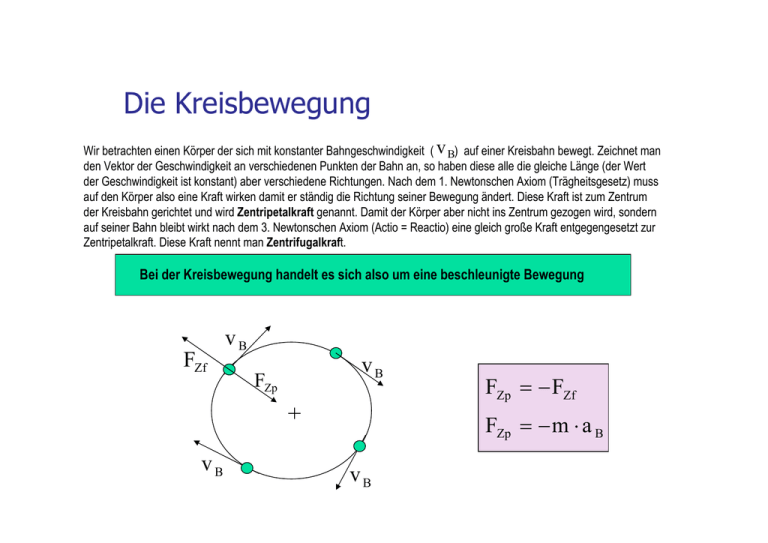
Die Kreisbewegung
Wir betrachten einen Körper der sich mit konstanter Bahngeschwindigkeit ( v B) auf einer Kreisbahn bewegt. Zeichnet man
den Vektor der Geschwindigkeit an verschiedenen Punkten der Bahn an, so haben diese alle die gleiche Länge (der Wert
der Geschwindigkeit ist konstant) aber verschiedene Richtungen. Nach dem 1. Newtonschen Axiom (Trägheitsgesetz) muss
auf den Körper also eine Kraft wirken damit er ständig die Richtung seiner Bewegung ändert. Diese Kraft ist zum Zentrum
der Kreisbahn gerichtet und wird Zentripetalkraft genannt. Damit der Körper aber nicht ins Zentrum gezogen wird, sondern
auf seiner Bahn bleibt wirkt nach dem 3. Newtonschen Axiom (Actio = Reactio) eine gleich große Kraft entgegengesetzt zur
Zentripetalkraft. Diese Kraft nennt man Zentrifugalkraft.
Bei der Kreisbewegung handelt es sich also um eine beschleunigte Bewegung
FZf
vB
FZp
vB
FZp = − FZf
FZp = − m ⋅ a B
vB
vB
Herleitung der Gesetze der Kreisbewegung
Berechnung der Bahngeschwindigkeit einer Kreisbewegung
Der Weg den der Körper bei einer vollen Runde zurücklegt ist gleich dem Kreisumfang
sK = 2 ⋅ π ⋅ r
Die Zeit die der Körper dafür braucht nennt man Umlaufzeit T. Die Geschwindigkeit die der Körper auf seiner Bahn hat
berechnet sich zu;
vB =
sK
T
vB =
2⋅π⋅r
T
Berechnung der Bahnbeschleunigung einer Kreisbewegung
vB
vB
vB
vB
vB
vB
vB
vB
Verschieben wir nun die Vektoren der Bahngeschwindigkeit alle zum Mittelpunkt des
Kreises, so können wir einen neuen Kreis um die Spitzen zeichnen mit dem Radius
v B . Die Umlaufgeschwindigkeit der Vektorspitze in diesem Kreis ist die
Bahnbeschleunigung . Die Umlaufzeit T ist in beiden Kreisen gleich.
2 ⋅ π ⋅ vB
aB =
T
4 ⋅ π2 ⋅ r
aB =
T2
Die Zentripetal und Zentrifugalkraft
FZp = − FZf
FZp = − m ⋅ a B
4 ⋅ π2 ⋅ r
aB =
T2
4 ⋅ π2 ⋅ r
FZp = m ⋅
T2
4 ⋅ π2 ⋅ r
FZf = − m ⋅
T2
Die Zentrifugalkraft spielt in der Technik eine große Rolle. Sie findet ihren Einsatz in der Wäscheschleudern
in der Industrie zur Stofftrennung (Butterherstellung, Blutkonserven, ...). Auch sind Spielgeräte auf den
Jahrmärkten sehr beliebt, die hohe Zentrifugalkräfte erzeugen (Achterbahn). Im Straßenverkehr beim
Kurvenfahren muss man allerdings darauf achten, dass die Zentrifugalkraft nicht zu groß wird und zum
Unfall führt.
Aufgabe Zentrifugalkraft
Wie groß ist die Beschleunigung die ein
Fahrgast aushalten muss, wenn er eine
Schleife der Achterbahn in 4s durchfährt.
Der Durchmesser der Schleife ist 16m.
Vergleiche das mit der normalen
Erdbeschleunigung.
4 ⋅ π2 ⋅ r
aB =
T2
2 ⋅ π2 ⋅ d
aB =
T2
2 ⋅ π 2 ⋅16 ⋅ m
aB =
(4 ⋅ s) 2
2 ⋅ π2 ⋅ m
aB =
s2
m
a B = 19,47 2
s
aB = 2⋅g
Die schiefe Ebene
Beim Heben schwerer lasten bedient sich der Mensch seit Jahrtausenden einer Vorrichtung die die
erforderliche Kraft verringert. Diese Vorrichtung nennen wir schiefe Ebene.
Mit Hilfe der Zerlegung von Kräften können wir das Wirkprinzip der schiefen Ebene erklären.
s
FN
FG
FH
h
FN
Normalkraft (Kraft die rechtwinklig auf
der schiefen Ebene steht)
FH
Hangabtriebskraft (Kraft die parallel zur
schiefen Ebene verläuft)
FG
Gewichtskraft (Kraft die senkrecht nach
unten wirkt)
Alle drei Kräfte bilden ein zur schiefen Ebene ähnliches Dreieck
FG
s
=
FH
h
s Länge der Hypotenuse
h Länge der Ankathete
Die Reibung
Wenn wir versuchen zwei sich berührende Körper gegeneinander zu verschieben, so müssen wir eine
Kraft aufbringen. Diese Kraft ist entgegengesetzt der wirkenden Kraft und heißt Reibungskraft.
Zugkraft
Reibungskraft
Die Reibung spielt überall in der Natur und Technik eine große Rolle. Sie wirkt einerseits störend und
sogar zerstörend aber andererseits ist die Natur und Technik auf ihr Vorhandensein angewiesen.
Versuche zur Reibung
Versuch 1
Wir ziehen einen rauen Holzquader der Masse 200g gleichmäßig über eine raue Holzunterlage. Die dazu
notwendige Kraft messen wir mit einer Federwaage. Wir wiederhohlen den Versuch mit einem rauen
Holzquader der Masse 400g und 800g.
Versuch 2
Wir ziehen einen rauen Holzquader der
Masse 200g gleichmäßig über eine
Glasplatte. Die dazu notwendige Kraft
messen wir mit einer Federwaage. Wir
wiederhohlen den Versuch mit einem
Holzquader der Masse 400g und 800g.
Versuch 3
Wir ziehen einen polierten Holzquader
der Masse 500g gleichmäßig über eine
polierte Holzunterlage. Die dazu
notwendige Kraft messen wir mit einer
Federwaage. Wir wiederhohlen den
Versuch mit einem Holzquader der
Masse 400g und 800g
Versuche zur Reibung
Versuch 3
Wir ziehen Holzquader gleicher Masse (500g) aber unterschiedlicher Grundfläche gleichmäßig über eine
Holzunterlage. Die dazu notwendige Kraft messen wir mit einer Federwaage.
Beobachtungen:
Die Reibungskraft ist unabhängig von der
Fläche die an der Reibung beteiligt is.
Beobachtungen zur Reibung
Beobachtungen:
Die Reibungskraft ist abhängig von der Normalkraft die der Körper auf die Unterlage ausübt.
Zugkraft
Reibungskraft
FR ~ FN
Normalkraft
Beobachtungen:
Die Reibungskraft ist abhängig vom Material der Körper (Holz, Glas, Stahl) und von der
Beschaffenheit der Oberflächen der Körper (rau, poliert).
FR
~ Oberflächeneigenschaft der Reibpartner
Beobachtungen:
Bei allen Versuchen haben wir beobachtet, dass die Kraft zum losreißen des Körpers größer ist als
die Kraft um ihn in Bewegung zu halten.
Es gibt zwei Reibungsarten Haftreibung und Gleitreibung
Gesetzmäßigkeiten der Reibung
Die Reibung zwischen zwei Körpern ist abhängig von den Oberflächeneigenschaften dieser Körper und
von der Kraft mit der die zwei Körper zusammengepresst werden. Weiterhin müssen wir unterscheiden
ob die Körper relativ zueinander in Ruhe sind oder sich bewegen.
FR = µ a / b ⋅ FN
Gleitreibung
FGR = µ aGR/ b ⋅ FN
µa /b
Haftreibung
FHR = µ aHR/ b ⋅ FN
Reibungskoeffizient zwischen der Oberfläche des Körpers a und der Oberfläche des Körpers b
Reibung in Technik und Natur
Notwendig:
Notwendig:
Autoreifen auf der Straße
Bremsen und Kupplung beim Auto
Riemenantriebe
Fortbewegung der Landtiere
Landschaftsbildung
Nachteil:
Bei zu wenig Reibung
Lawinen und Erdrutsche
Kugellager
Kolbenbewegung beim Motor
Überall wo man schmieren muss
Nachteil:
Reibungskoeffizienten
Werkstoff a
Holz
Gummi
Gummi
Metall
Stahl
Stahl
Werkstoff b
Holz
Asphalt
Beton
Holz
Eis
Stahl
Haftreibung
0,65
0,9
1
0,55
0,02
0,15
Gleitreibung
0,35
0,3
0,5
0,35
0,01
0,1
Impuls
Wirkt auf einen Körper der Masse „m“ für eine kurze Zeit „t“ die Kraft „F“, so erfährt dieser Körper nach dem
2. Newtonschen Axiom in dieser Zeitspanne eine Beschleunigung. Diesen Kraftstoß nennt man auch Impuls.
Nach Ende des Kraftstoßes hat der Körper die Geschwindigkeit „v“ erreicht.
Mathematisch kann man diesen Sachverhalt folgendermaßen schreiben:
F ⋅t = m⋅a ⋅t
mit
„t“ kann gekürzt werden
erhält man
v
a=
t
erhält man
F ⋅t = m⋅v
p = m⋅v
v
F ⋅t = m⋅ ⋅t
t
und mit
F ⋅t = p
die Beziehung für den Impuls
Der Impuls eines Körpers ist dessen Masse, multipliziert mit seiner Geschwindigkeit
Impulserhaltung
Mit dem Impuls verhält es sich ähnlich wie mit den Kräften, man kann ihn nicht sehen, vor allem nicht, wenn man
sich im Bezugssystem des Körpers befindet.
Der Impuls entfaltet seine Wirkung erst, wenn er mit anderen Körpern wechselwirkt. Der Impuls kann auch nicht
verloren gehen ( wenn er nicht in Wärme oder bleibender Materialverformung umgewandelt wird). Der Impuls kann
nur von einem Körper auf einen anderen übertragen werden. Die Summe der Impulse in einem abgeschlossenen
System bleibt konstant. Der Impuls hat den Charakter eines Vektors, genau wie die Geschwindigkeit.
Im Versuch kann man demonstrieren, dass sich das System Reagenzglas Korken, welches sich in Ruhe befindet, also
den Impuls „0“ besitzt, auch nach dem Korken und Reagenzglas in entgegengesetzte Richtungen wegfliegen, den Impuls
„0“ besitzt.
Vorher:
p k = 0; p R = 0
Nachher:
m K ⋅ v K = −m R ⋅ v R
pK + pR = 0
Das Raketenprinzip
Das 3. Newtonsche Gesetz erlaubt es den Impuls zum antreiben von Raketen und Flugzeugen einzusetzen. Beim
Ausstoßen der Verbrennungsgase übertragen diese ihren Impuls auf den Flugkörper und bewegen diesen in die
entgegengesetzte Richtung.
v Fk =
m gas ⋅ v gas
m Fk
Da sich die Masse des Flugkörpers aber ständig
Ändert, wird diese Gleichung kompliziert.
Raketengleichung von Konstantin Ziolkowski
pGas = p Flugkörper
m gas ⋅ v gas = m Flugkörper ⋅ v Flugkörper
Константин Циольковский
(1857-1935)
Konstantin Eduardowitsch Ziolkowski wurde am 17. September 1857 in Russland geboren. Er gilt als
Vater der modernen Raumfahrt.
Konstantin studierte Physik, Astronomie, Mechanik und Geometrie in Moskau. Während einer
Vorlesung in Physik lernte er die Newtonschen Gesetzte kennen. Als er das dritte Gesetz, wonach jede
Kraft eine gleichgroße Gegenkraft erzeugt, deren Richtung der ersten Kraft entgegengesetzt ist, hörte,
war ihm klar, dass die Lösung für den Flug in den Weltraum die Rakete mit ihrem Rückstoßprinzip sein
musste.
Konstantin Ziolkowski stellte die ersten Berechnungen über die Möglichkeit interplanetarer Flüge und
über den Abschuss künstlicher Satelliten auf eine Erdumlaufbahn auf.
Er erkannte, dass die bisher bekannten Feststoffraketen, die für Feuerwerke und als Kriegsraketen
verwendet wurden, zu schwach sein würden, um den Weltraum zu erreichen. Eine größere Leistung
bedeutet eine höhere Ausströmgeschwindigkeit der Verbrennungsgase. Konstantin Ziolkowski war klar,
dass dies nur mit flüssigen Treibstoffen zu erreichen war. Im Jahre 1898 schlug er als Erster die
Verwendung von flüssigen Raketentreibstoffen (Wasserstoff, Sauerstoff und Kohlenwasserstoff) vor. Er
hatte verschiedene Entwürfe für gebündelte Raketen und Mehrstufenraketen vorgeschlagen, mit denen
man sehr große Höhen erreichen konnte. Es war ihm nicht vergönnt, zu Lebzeiten die praktische
Umsetzung seiner Ideen zu erleben.
Russische Stufenrakete Sojus
Amerikanische Ariane Rakete