Document

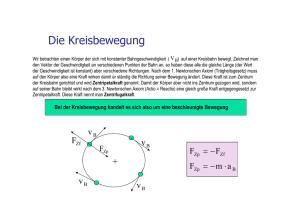
19
3. Dynamik
20
Nachrechnen:
v 1m/s
=
= 1 m/s 2
t
1s
F = mt a = 1 kg 1 m/s 2 = 1 N
Die Dynamik befasst sich mit den Ursachen der Bewegung.
3.1 Axiome
a=
3. Reaktionsprinzip (actio gleich reactio) (Newton)
1. Trägheitsprinzip (Galileo, 1564-1642
Newton, 1643- 1727)
Ein sich selbst überlassener Körper bewegt sich geradlinig
gleichförmig
Die Wirkungen (Kräfte) zweier Körper aufeinander sind
stets gleich groß und von entgegengesetzter Richtung
F1
F2
F2 = − F1
(ohne Kraft keine Änderung der Bewegungsrichtung oder
Geschwindigkeit)
2. Aktionsprinzip (Newton)
Ursache einer Änderung des Bewegunszustands eines
Körpers ist eine Kraft F die der Beschleunigung a
proportional ist. Die Proportionalitätskonstante heisst
die träge Masse des Körpers.
also:
F = mt a
Die Einheit der Kraft ist Newton: [N] = [kg m/s2]
Eine Kraft von 1 N beschleunigt 1kg in 1s auf 1m/s.
3.2 Schwere und träge Masse
Die Anziehung durch die Erde bewirkt eine Kaft Fg auf einen
Körper, die proportional zu seiner schweren Masse ist:
Fg = ms g
Gewichtskraft
ms
Fg
21
22
3.3 Vektorielle Addition von Kräften
Dies bewirkt eine Beschleunigung
Fg
m
a=
= sg=g
mt mt
(falls ms = mt)
Kräft haben Richtung und Betrag. Mehrere an einem Punkt
angreifende Kräfte werden vektoriell addiert:
F
F = F1 + F2
Experimente zeigen, dass die schwere Masse tatsächlich
gleich der trägen Masse ist
Hierbei gilt:
F1
F2
F ≤ F1 + F2
⇒ alle fallenden Körper beschleunigen mit g
Experiment: Entkopplung von beschleunigter und
Kraft erzeugender Masse
Die Gesamtkraft ist immer kleiner oder gleich
der addierten Einzelkräfte
Beispiele:
F
spitzer
Winkel:
m2
Kraft
flacher
Winkel:
F 1 = m1 g
beschleunigt Masse m = m1 + m2
F
F2
F ≈ F1 + F2
F1
F2
F << F1 + F2
Beschleunigung:
Experiment:
F
m1 g
a= =
m m1 + m2
m1
Tabelle:
m1
m2
a
m0
m0
1/2 g
10 m0
m0
10/11 g
m0
10 m0
1/11 g
F1
Rechter Winkel wegen
Pythagoras:
F2
5 = 4 2 + 32
F3
4m0 g
5m0 g
hier:
3m0 g
F =
2 2
F1 + F2
F1
23
3.3 Aufteilung von Kräften
F1
F2
Beispiel: schiefe Ebene
F
h
⊥
F
l
Für kleine Winkel α gilt:
α
Damit:
h
l
a=
⊥
Gewichtskraft wird aufgeteilt
F
in anpressende Kraft Fund
beschleunigende Kraft
(„Hangabtriebskraft“)
3.5 Kreisbewegung: Beschleunigung
y
Es ist
mg sin α
m
= g sin α
Beschreibung des Orts und der
Geschwindigkeit:
r
|F | = F = F sin α
g
ϕ
=
h
g
l
Bei kleinen Steigungen ist die Beschleunigung gleich
Erdbeschleunigung mal Steigung!
Fg = mg
Beschleunigung:
a = F
m
sin α ≈ tan α =
=
F = F1 + F2
m
1
s = sin α gt 2
2
zurückgelegter Weg:
Ein Kraftvektor kann immer als Summe von Kraftvektoren
dargestellt werden:
F
24
Beschleunigung:
Entspricht freiem Fall mit verminderter Schwerkraft!
also:
x
 r0 cos ωt 
 − r ω sin ωt 
 d  0


r =  r0 sin ωt  ; v = r =  r0ω cos ωt 
dt




0
 0 


 − r0ω 2 cos ωt 

d 
a = v =  − r0ω 2 sin ωt 
dt


0


a (t ) = −ω 2 r (t )
25
Bei der Kreisbewegung verändert sich die Geschwindigkeit
ständig; es wirkt eine konstante, auf das Kreiszentrum
gerichtete Beschleunigung.
26
Beispiel: Kettenkarussel
ω
a (t ) = a = ω 2 r0
Betrag:
v=
mit Bahngeschwindigkeit
a = ω 2 r0 =
− Fg
2πr0
τ
2πr0
=
= r0ω
2π / ω
Fzp
Momentaufnahme
Fk
Fzp
m
Es gilt:
Fk = (− Fg ) + Fzp
Fg = mg
2
v
r0
negative
Schwerkraft
Ursache der Beschleunigung ist eine Kraft:
v
Die Kraft wird durch
die Kette erzeugt (Richtung
parallel zur Kette)
Kette
Zentripetalkraft
Kraft auf den Körper:
F = Fk + Fg = (− Fg ) + Fzp + Fg = Fzp
Fzp = ma = −mω 2 r
Die Kraft der Kette wirkt der Schwerkraft entgegen (verhindert
Fallen des Körpers) und bewirkt eine Beschleunigung „nach innen“
(verursacht Kreisbewegung).
Zentripetalkraft
v2
Fzp = Fzp = mω 2 r0 = m
r0
Die Kraft hält den Körper auf der Kreisbahn (ohne Kraft
würde er sich geradlinig bewegen!)
Der Winkel der Kette zeigt die Stärke der Kreisbeschleunigung an:
− Fg
α
Fzp
tan α =
Fzp
g=
Fg
=
mazp
mg
a zp
tan α
Je größer der Winkel, desto größer die Kreisbeschleunigung!
27
3.6 Zentripetal- und Zentrifugalkraft
− Fg
Fk
Fzp
Gleiches Bild, aber aufgenommen
im System des Karussells; hier ist
alles in Ruhe
m
Fzf
28
Die Zentrifugalkraft ist eine „Scheinkraft“, da sie nicht auf der
Wechselwirkung zwischen Objekten beruht; sie hat aber die
gleiche Wirkung wie eine „reale“ Kraft.
Merkregel:
Beschreibung der Kraft in einem
rotierenden System
• Beobachter ruht: Zentripetalkraft
Fg = mg
• Beobachter rotiert mit: Zentrifugalkraft
Grund: im rotierenden Bezugssystem wirkt eine weitere Kraft,
die Zentrifugalkraft:
Fzf = − Fzp
3.7 Künstliche Schwerkraft
Kraft im rotierenden System wirkt wie (veränderte) Schwerkraft
Damit ist die Gesamtkraft auf den Körper:
F = Fg − Fg + Fzp + Fzf = 0
und damit:
a=
1 F =0
m
(der Körper bleibt in seinem Zustand der Ruhe)
Im rotierenden Bezugssystem wirkt eine nach außen
(weg von der Rotationsachse) gerichtete Kraft
v2
2
Fzf = mω r = m
r
Zentrifugalkraft (Fliehkraft)
hier:
m
Fges = Fzf + mg = mg '
Fzf
Fg
g ' = g ' = (ω 2 r ) 2 + g 2
Fges
g
g'
Die „künstliche Schwerkraft“ kann viel größer sein als g!
Beispiel: Waschmaschine, Schleudergang
Radius: 0.25 m
1400 Umdrehungen/min:
1400
1
= 23.3
60s
s
1
ω = 2πf = 147
s
f =
29
Zentrifugalbeschleunigung damit:
a = rω 2 = 5373
30
3.8 Gravitationswechselwirkung
m
= 548 g
s2
Zwischen zwei Körpern der Masse m1 und m2 im Abstand r
wirkt eine anziehende Kraft:
(Menschen überleben kurzzeitig 20 g!)
r
F =G
Beispiel: Erddrehung
ω
Radius:
Frequenz:
Fg
Fzf
r = 6400 km
1
1
f =
= 11.6 ×10−6
24h
s
1
ω = 2πf = 73×10−6
s
a zf = ω 2 r = 0.03
Erde
m
s2
m1
m2
Beispiel: Erde
rE = 6378 km
m2
g ' = g − ω r = 0.997 g
2
mE = 5.98 1024 kg
r
F =G
(am Äquator wirken Schwere- und Zentrifugalbeschleunigung
in Gegenrichtung, daher wird hier die Differenz genommen).
Erde (mE)
Die Zentrifugalbeschleunigung aufgrund der Erddrehung ist
aso sehr klein. Aber: hätte ein Erdtag 1.4h, wäre ω2r=g und
g‘=0 !
G: Gravitationskonstante
G = 6.67 10-11 Nm2/kg2
(am Äquator)
Hier ist:
m1m2
r2
mE m2
m
= G E2 m2
2
rE
rE
m
= 9.805  2  m2 = g m2
s 
Erdbeschleunigung g = 9.81 m/s2 gilt nur auf der Erdoberfläche!
(nimmt quadratisch ab mit dem Abstand zum Erdmittelpunkt)
31
Beispiel: Mond
rM = 1738 km
32
in beiden Fällen (falls m1 >> m2 ) :
m1m2
r2
m
ω 2 = G 31
r
m2 rω 2 = G
mM = 7.35 1022 kg
m2
r
gM = G
mM
m 1
=
1
.
6
2
 s 2  ≈ 6 g
rM
Die Umlauffrequenz ist unabhängig von m2 !
Mond (mM)
Mit
Die Gravitationsbeschleunigung ist auf der Mondoberfläche etwa
sechsmal kleiner als auf der Erdoberfläche.
Also:
ω=
2π
τ
2
4π 2 3
r
τ =
Gm1
2
3.9 Satelliten
Fg
m1
m2
3. Keplersches
Gesetz
Die Quadrate der Umlaufzeiten sind proportional der
Kuben der Bahnradien (doppelter Radius → 2.8 fache Umlaufzeit).
v = rω
r
m1
 2π 
  =G 3
r
τ 
wird dies zu:
Kreisbewegung einer Masse m2
um eine Masse m1, verursacht
durch Gravitationswechselwirkung.
Bemerkung: das Keplersche Gesetz gilt nicht nur für Kreisbahnen,
sondern auch für elliptische Bahnen; hier ist r die Länge der großen
Halbachse der Bahn
Beispiel: Raumstation ISS
Es gilt:
Flughöhe: 400 km
Bahnradius: r = rE + 400 km = 6800 km
Zentripetalkraft = Gravitationskraft
(ruhender Beobachter)
Zentrifugalkraft = -Gravitationskraft
ω=
GmE
1
= 1.1 ⋅10 −3
3
s
r
τ=
2π
ω
(mitbewegter Beobachter)
Bahngeschwindigkeit:
v = rω = 7660
= 5560 s = 1.5 h
m
km 
 = 27600 !
s
h 
33
Beispiel: Erdmond
Bahnradius: r = 3.84 108 m (384000 km)
ω=
GmE
−6 1
=
⋅
2
.
65
10
s
r3
τ=
2π
ω
= 2.4 ⋅106 s = 27.4 d
v = rω = 1019
Bahngeschwindigkeit:
m
s
Beispiel: Erdbewegung um Sonne
Bahnradius: r = 149.6 109 m (150 Mio km)
Sonnenmasse: mS = 1.99 1030 kg
ω=
GmS
−9 1
=
⋅
199
10
s
r3
Bahngeschwindigkeit:
τ=
2π
ω
= 3.15 ⋅107 s = 365.2 d
v = 29700
m
km 
 = 107000 !
s
h 
Weitere Planeten (bzw. Planetoiden):
Merkur
r = 57.9 109 m
τ = 88 d
Jupiter
r = 778 109 m
τ = 11.6a
Pluto
r = 5910 109 m
τ = 249a