Folien

Die Binomialverteilung
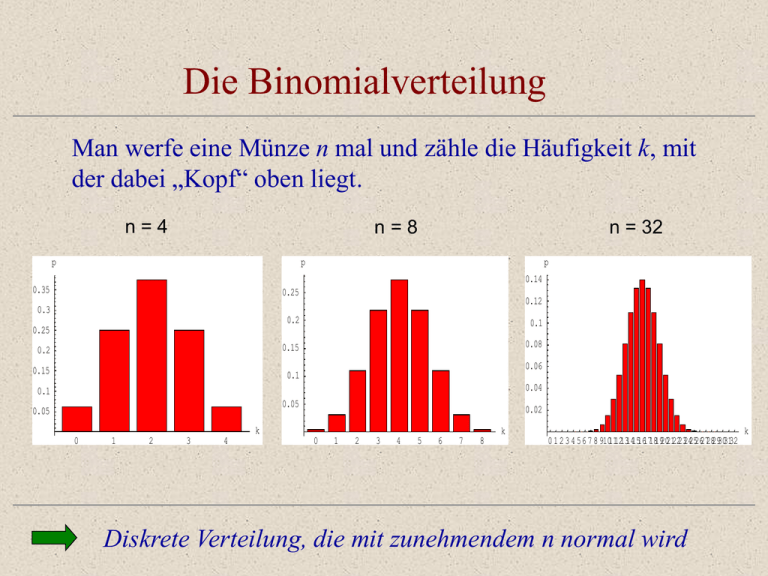
Man werfe eine Münze n mal und zähle die Häufigkeit k, mit
der dabei „Kopf“ oben liegt.
n=4
n=8
n = 32
p
p
p
0.14
0.35
0.25
0.3
0.12
0.2
0.1
0.2
0.15
0.08
0.15
0.1
0.25
0.06
0.04
0.1
0.05
0.05
0
1
2
3
4
k
0.02
0
1
2
3
4
5
6
7
8
k
0 1 2 3 4 56 7 8 91011121314151617181920212223242526272829303132
Diskrete Verteilung, die mit zunehmendem n normal wird
k
Die Binomialverteilung
Man wiederhole ein Zufallsexperiment n mal und bestimme
die Häufigkeit k, mit der ein bestimmtes Ereignis E eintritt.
Es sei:
PE  p
PE  1 p  q
Bei n Wiederholungen kann das Ereignis „k-mal E“ auf genau
 n  Weisen eintreten. Da sich die einzelnen n über k Folgen
k 
  gegenseitig ausschliessen, folgt mit dem Additionssatz:
 n  k n k
P k n      p  q
k 
[Tafel-Entwicklung]
Multiplikationssatz der WKn für unabhängige Versuche & Additionssatz auf die
disjunkten Folgen anwenden!
Die Verteilungsfunktion der Binomialverteilung
Die Wahrscheinlichkeit, daß höchstens k mal E auftritt, ist:
ænö
÷ p j ×q nP ( j £ k n) = å çç ÷×
÷
ç ÷
j= 0 è jø
k
j
Die Wahrscheinlichkeit, daß mindestens k+1 mal E auftritt,
ist:
n æ ö
n÷ j n- j
ç
P ( j ³ k + 1 n) = å ç ÷×
p ×q
÷
çè j ø
÷
j= k + 1
= 1 - P ( j £ k n)
Binomialverteilung: Diskrete Wahrscheinlichkeitsverteilung
Wahrscheinlichkeitsfunktion
Definition:
æn÷
ö x n- x
f n (x) = çç ÷×
p ×q
÷
çèx÷
ø
definiert die Wahrscheinlichkeitsfunktion, oder
Wahrscheinlichkeitsdichtefunktion der Binomialverteilung.
Sie tritt auf bei der Betrachtung der Anzahl der Erfolge einer Folge von unabhängigen Versuchen (Bernoulli-Folge), wobei p die Wahrscheinlichkeit des Erfolgs bei
einem Versuch ist und q = 1- p gilt. n ist die Anzahl der Wiederholungen des Versuchs. p und n sind die beiden Parameter der Binomialverteilung
Binomialverteilung: Diskrete Wahrscheinlichkeitsverteilung
mit den Parametern p und n.
Verteilungsfunktion
Definition:
æn÷
ö k n- k
ç
Fn (x) = å ç ÷×
p ×q
÷
ç
÷
k = 0 èk ø
x
definiert die Verteilungsfunktion der Binomialverteilung.
Allgemein:
x
Fn (x) = P (k £ x n) =
å
f n (k )
k= 0
Die Verteilungsfunktion ist die kumulierte Wahrscheinlichkeitsdichtefunktion. Sie
gibt die Wahrscheinlichkeit für Erfolge bis zu einer oberen Schranke x an.
Verteilungsfunktion: Kumulierte Wahrscheinlichkeitsdichtefunktion bis zu einer Grenze x.
Verteilungsfunktion für diskrete Variable
Es gilt für diskrete Zufallsvariablen:
f n (x)= Fn (x)- Fn (x - 1)
Allgemeine Eigenschaften sind:
1. Fn (x0 ) = 0, für x0 < min {x}
2. Fn (x0 ) = 1, für x0 = max {x}
3. P (xu < x £ xo ) = Fn (xo )- Fn (xu )
Mit der Verteilungsfunktion kann man die Wahrscheinlichkeit
für beliebige Intervalle der Zufallsvariable bestimmen.
Die Poissonverteilung
Sind einzelne Ereignisse selten, so kann die Wahrscheinlichkeit
statt mit der Binomialverteilung über die Poissonverteilung
ausgedrückt werden.
Gilt:
  n p  5
So approximiert die Possonverteilung die Binomialverteilung gut.
Die poissonverteilung hat nur den Parameter , der
sowohl Mittelwert wie Varianz beschreibt.
Wahrscheinlichkeitsfunktion:
f  x 
 x e 
x!
Die Poissonverteilung ist eine einfache Alternative zur Binomialverteilung für
Seltene Ereignisse.
Vergleich: Binomial - Poisson
Poissonverteilung
0.5000
0.5000
0.3750
0.3750
WK
WK
Binomialverteilung
0.2500
0.2500
0.1250
0.1250
0.0000
0.0000
0
1
2
3
4
5
6
7
8
0
Erfolge
Für
n  100
1
2
3
4
Erfolge
p  0.012
  n  p  1.2
Fast exakte Übereinstimmung beider Verteilungen.
5
6
7
8
Die Normalverteilung
f (x)
0.04
0.03
1
f  x 
e
s  2
0.02
1  x x 
 

2 s 
2
0.01
20 25 30 35 40 45 50 55 60 65 70 75 80
x
Die Normalverteilung (Gauss‘sche Glockenkurve) ist eine symmetrische
Verteilung. Ihre Form ist durch die Standardabweichung und den
Mittelwert eindeutig festgelegt. Sie resultiert aus dem Modell
unabhängiger sich überlagernder Zufallsfehler („Galton-Brett“)
[Tafelbeispiel Galton, Binomial]
Die Normalverteilung
F(x)
1.0
1
F (x)=
s × 2p
0.75
0.5
x
2
1æ
u- x ö
÷
ç
- ×ç
÷
÷
2 çè s ø
òe
- ¥
0.25
20 25 30 35 40 45 50 55 60 65 70 75 80
x
Die Verteilungsfunktion der Normalverteilung (Fläche unter der
Normalkurve) kann man nicht auf eine geschlossene Form bringen. Sie
ist aber für standardisierte Variablen (z-Standardisierung) austabelliert
und elektronisch implementiert (z.B. in Excel).
du
Die Normalverteilung
f(z)
f(z)
0.4
-3
-2
-1
0.4
68.26%
0.3
0.3
0.2
0.2
0.1
0.1
1
2
xx
z
s
3
z
-3
-2
-1
95.5%
1
2
3
1  12 z 2
f  z 
e
2
Die Fläche unter der Kurve ist bei der Normalverteilung eine Funktion
der Standardabweichung (in Einheiten von s angebbar)
[Tabellenbenutzung, Excel, Aufgabenbeispiel zu IQ‘s]
z
z - Standardisierung
Wahrscheinlichkeitsdichte
0.10
x
0.05
0.00
-15
-10
-5
0
x
5
10
15
f (z)
Wahrscheinlichkeitsdichte
xx
z
s
f  x
x
0.10
z 1
0.05
0.00
-3z
-2z
-1z
0
1z
2z
3z
zx
z - Standardisierung zur Überführung in Standardnormalverteilung
z
Wahrscheinlichkeitsbestimmung
Verteilungsfunktion
(Fläche der Dichtefunktion)
F  z0   P  z  z0 
Eigenschaften
F    0
F    1
P  za  z  zb   F  zb   F  za 
za
 Benutze austabellierte Standardnormalverteilung
zb
Approximation der Binomialverteilung
Die Binomialverteilung hat ebenfalls Mittelwert und Varianz:
  n p
 2  n pq
Gilt n  p  q  9 so kann die Binomialverteilung durch die
Normalverteilung approximiert werden.
Dann gilt B  n; p 
[Beispiele]
N   ; 
Fehler 1. und 2. Art
In der Population gilt
H0
Entscheidung für
H1
H0
H1
Correct
Rejection
P  H0 H0 
Miss
(Fehler 2. Art)
P  H 0 H1 
False Alarm
(Fehler 1. Art)
P  H1 H 0 
Hit
P  H 1 H1 
Hypothesenwahrscheinlichkeiten : bedingte WKn
Mittelwerteabstand aus WK
Man klassifiziere man nach „Distraktor“ (H0) und „Target“ (H1)
Tatsächlich gilt
H0
Entscheidung für
H1
H0
H1
P  H0 H0 
P  H 0 H1 
0.59
P  H1 H 0 
0.077
P  H 1 H1 
0.41
0.923
1
1
Wie groß ist der Mittelwerteabstand der Likelihoodfunktionen ?
Mittelwerteabstand
H0 – Verteilung:
H1 – Verteilung:
0.4
0.4
-3
-2
pp == 0.077
0.59
0.3
p = 0.59
-1
0.3
0.2
0.2
0.1
0.1
1
2
3
-3
z0 = F-1{0.59} = 0.23
Correct Rejection
z - Berechnung für jede einzelne Verteilung
-2
-1
1
2
3
z1 = F-1{0.077} = -1.43
Miss
Abstand in z- Standardisierung
Es gilt:
z0 
k  0
Ferner:

z1 
k  1
Nun betrachte im z1 Wert den Abstand des Kriteriums k in Bezug auf 0:
z1 
k   0   1  0  


k  0

1  0


z1  z0  d '
d '  z0  z1
(standardisierter Abstand)
Annahme: beide Likelihoodfunktionen haben dieselbe Varianz
