Kapitel 14: GRÖßE UND STRUKTUR VON MOLEKÜLEN Einleitung
Werbung

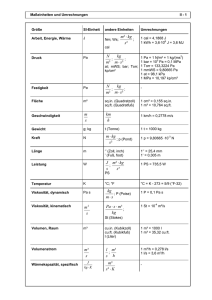
Kapitel 14: GRÖßE UND STRUKTUR VON MOLEKÜLEN Inhalt: EINLEITUNG ............................................................................................................................ 223 EINIGE METHODEN ZUR CHARAKTERISIERUNG BIOLOGISCHER MAKROMOLEKÜLE ............................ 223 DEFINITION STOFFMENGE......................................................................................................... 224 DEFINITIONEN FLÜSSIGKEITEN ................................................................................................... 225 OSMOTISCHER DRUCK ............................................................................................................. 225 ZENTRIFUGATION .................................................................................................................... 227 ELEKTROPHORESE .................................................................................................................... 242 RÖNTGENSTRUKTURANALYSE .................................................................................................... 252 KERNRESONANZSPEKTROSKOPIE (NMR) ..................................................................................... 254 STRÖMUNG UND VISKOSITÄT.................................................................................................... 255 LITERATUR .............................................................................................................................. 265 Einleitung Größe und Struktur bestimmen die Wahrscheinlichkeit für das Eintreten chemischer Reaktionen zwischen den Molekülen; sie bestimmen aber auch die Beweglichkeit der Moleküle im umgebenden Medium, den Transport durch Membranen, und die Fähigkeit, Information zu speichern und zu transportieren. Es gibt zahlreiche Methoden, mit denen unterschiedlichen Kriterien ermittelt werden. die Eigenschaften der Moleküle nach Einige Methoden zur Charakterisierung biologischer Makromoleküle Methode Aussagen über Osmotischer Druck Diffusionskoeffizient Sedimentationsgeschwindigkeit Sedimentationsgleichgewicht Elektrophorese Elektronenmikroskopie Elektronenbeugung Lichtstreuung Röntgenlichtstreuung Ar oder Mr molekulares Volumen molekulares Volumen Ar oder Mr Ladung, Form und Größe Form und Größe zwischenmolekulare Räume molekulare Anisotropie und Ar Form und Größe 223 GRÖßE UND STRUKTUR VON MOLEKÜLEN Röntgeninterferenz Viskosität Strömungsdoppelbrechung elektrische Doppelbrechung dielektrische Dispersion Rotationsdispersion Kernmagnetresonanz (NMR) Lage der Atome Molekülform + gebundenes Wasser Molekülform + gebundenes Wasser Molekülform + gebundenes Wasser Molekülform + gebundenes Wasser Helixstrukturen Molekülstruktur (Tomographie) Definition Stoffmenge Die Größe Stoffmenge mi beruht auf der "Abzählbarkeit" einzelner Teilchen (Atome, Moleküle, Radikale, Ionen, Elektronen, Nukleonen, Photonen). Die Einheit der Stoffmenge ist das Mol [mol]. Die Stoffmenge 1 mol enthält bei allen Stoffen die gleiche Anzahl von Teilchen (AvogadroKonstante): L = 6,02205 × 1023 mol-1 (Moleküle / 1 mol idealen Gases) Ein System mit der Stoffmenge 1 mol besteht aus ebenso vielen unter sich gleichen (oder als gleich betrachteten) Individuen, wie Atome in 0,012 kg des Kohlenstoffnuklids 12C enthalten sind. Die Masse eines Moleküls oder Atoms wird immer relativ zum Bezugsnuklid 12C angegeben. Die Angabe Atomgewicht oder Molekulargewicht ist daher nicht richtig, da nicht das Gewicht eines Atoms oder eines Moleküls bestimmt wird, sondern nur Atom- bzw. Molekülmassen miteinander verglichen werden. Man spricht daher von (relativer) Atommasse Ar oder (relativer) Molekülmasse Mr. Die Gesamtstoffmenge einer Mischung ergibt sich aus der Summation der einzelnen Stoffe. Ar = mi 12,000 m12C mi: mittlere Masse des Atoms der Sorte i im natürlichen Elementgemisch. Ar hat keine Einheit! Sie ist der Quotient aus zwei Massen! In der Molekularbiologie hat sich dafür die Angabe Dalton (d) eingebürgert. 224 BIOPHYSIK DER ZELLE Element Ar H 1,01 C 12,01 N 14,01 O 16,00 Beispiel: 3 M KCl Lösung enthält wieviel g KCl im Liter? Relative Atommasse von K: 39; von Cl: 35,5 -> molare Masse für KCl: 74,5 -> In einem Liter 3 M KCl Lösung sind 223,5 g KCl enthalten. Definitionen Flüssigkeiten Lösungsmittel Lösung gesättigte Lösung Mischung Suspensionen Emulsion Löslichkeit Konzentration einmolare Lösung einmolale Lösung Wasser, Alkohol Gemisch aus Lösungsmittel und gelöstem Stoff; echte Lösung, wenn jedes Molekül des gelösten Stoffes gleiche Anzahl Wassermoleküle anlagert Lösung nimmt keine Substanz mehr auf, wird mehr Substanz hinzugegeben, so fällt diese aus Flüssigkeiten können entweder in beliebigen Mengenverhältnissen (Wasser/Alkohol) oder nur in bestimmten Mengenverhältnissen (Wasser Äther) gemischt werden (Schichtung). Bei Mischung kann es zu starker Volumenänderung kommen (Wasser - Alkohol). Molekularkräfte innige Vermischung aber keine molekulare Verteilung der Substanz im Lösungsmittel; Teilchengröße kann auch im Bereich von kolloidalen Partikeln liegen. Blut Zwei nicht mischbare Flüssigkeiten (Öl / Wasser) Milch hängt von Druck und Temperatur der Lösung ab Menge Substanz pro Lösung Gewichtsprozente: (w/w) g Subst. / 100 g Lösung Gewicht/Volumen: (w/v) g Subst. / Vol. Lösung Volumenprozent: (v/v) ml Subst. / 100 ml Lösung in 1 l Lösung ist 1 Mol Substanz gelöst in 1000 g Lösungsmittel ist 1 Mol Substanz gelöst Osmotischer Druck Osmose ist die Diffusion von Molekülen durch eine semipermeable Membran. Trennt man eine Zuckerlösung von reinem Wasser durch eine semipermeable Membran, die nur Wassermoleküle passieren lässt, dann wird die Zuckerlösung im Laufe der Zeit durch die eindiffundierenden Wassermoleküle verdünnt. Mit der damit verbundenen Volumenzunahme ist eine hydrostatische Druckerhöhung verknüpft. Ein 225 GRÖßE UND STRUKTUR VON MOLEKÜLEN Gleichgewichtszustand stellt sich ein, wenn im zeitlichen Mittel keine Wassermoleküle mehr in die Zuckerlösung gelangen. Der dem hydrostatischen Druck entsprechende Druck der Lösungsmittelmoleküle, wie z. B. Wasser, heißt Osmotischer Druck. ∆p = ρ g ∆h Lösungsmittel impermeabler ∆h Osmolyt ∆c ∆π = RT ∆c Abb. 169: Pfeffersche Zelle semipermeable Membran Da verdünnte Lösungen wie ein Gas behandelt werden können, wird der osmotische Druck formal wie ein reales Gas beschrieben: Ideales Gas nach Boyle-Marriotte: pV=RT wenn N Mol des Gases betrachtet werden: pV=NRT Bei einem realen Gas: 2 N N p V = N R T 1 + B + C + .... V V wobei B und C als Virialkoeffizient bezeichnet werden. 226 BIOPHYSIK DER ZELLE Unter Berücksichtigung der van der Waals Kräfte lautet die Gleichung: a p + 2 (V - b ) = N R T V dabei ist V das Molvolumen, a/V2 der Innendruck und b das vierfache Eigenvolumen der Gasmoleküle. Der osmotische Druck π entspricht dem Druck p und die Konzentration der gelösten Substanz c entspricht der Anzahl N der Gasmoleküle. π =RTc Van't Hoffsches Gesetz (1886) Zentrifugation Die Auftriebskraft (Gesetz des Archimedes) Ein Körper, der in eine Flüssigkeit eingetaucht wird, zeigt einen scheinbaren Gewichtsverlust. Die Ursache ist eine Kraft, die der Gravitationskraft FG (= Gewichtskraft) entgegenwirkt: die Auftriebskraft FA. Mit zunehmender Tiefe nimmt der hydrostatische Druck in einer Flüssigkeit zu, daher wirkt auf einen in die Flüssigkeit gebrachten Körper auf seine Oberseite ein geringerer Druck als auf seine Unterseite. Diese Druckdifferenz bewirkt den Auftrieb, wie sich an einem rechtwinkeligen Körper mit der Höhe ∆ h zeigen lässt (Abb. 170). Allgemein gilt für den hydrostatischen Druck p: p = h ρL g h = Höhe, Entfernung von der Oberfläche ρ L = Dichte der Flüssigkeit; g = Erdbeschleunigung (= 9,81 ms-2) Abb. 170: Auftriebskraft FA Auf die Oberseite des Körpers in Abb. 170 wirkt der hydrostatische Druck: 227 GRÖßE UND STRUKTUR VON MOLEKÜLEN p oben = h 1 ρ L g und auf die Unterseite: p unten = h 2 ρ L g Da h1 < h2 ist auch p oben < p unten. Es ergibt sich ein resultierender Druck ∆ p, der nach oben gerichtet ist ∆ p = p unten - p oben = (h 2 - h 1 ) ρ L g = ∆ h ρ L g Die Fläche A des Körpers bestimmt mit dem Druck die resultierende Kraft FA (Auftriebskraft, da nach oben gerichtet) FA = A ∆ p = A ∆ h ρ L g Das Volumen der verdrängten Flüssigkeit ist gleich groß wie das des eintauchenden Körpers, nämlich V = A ∆ h . Die Masse der verdrängten Flüssigkeit ist daher m L = A ∆ h ρ L . Die Gravitationskraft FG der verdrängten Flüssigkeit (FG = m L g) ist also dem Betrag nach, aber nicht in der Richtung, gleich der statischen Auftriebskraft FA : FA = V ρ L g = m L g Sedimentation Ein Körper sinkt (sedimentiert) in einer Flüssigkeit, wenn die auf ihn wirkende Gravitationskraft FG größer ist als die Auftriebskraft FA. Eine solche Sedimentation erfolgt immer dann, wenn die Dichte des Körpers größer ist als die Dichte des Lösungsmittels. Dieser Zusammenhang lässt sich ebenfalls aus dem Archimedischen Gesetz herleiten: In der Flüssigkeit wirkt auf eine Partikel der Masse m p die Gravitationskraft FG FG = m p g und die Auftriebskraft FA, die der Gravitationskraft entgegengesetzt ist: FA = m L g Da das Volumen VP = mP ρP der eingetauchten Partikel und das Volumen VL = von ihm verdrängten Flüssigkeit gleich sind, folgt: 228 mL ρL der BIOPHYSIK DER ZELLE mP ρP = mL ρL mL = m P ρL ρP Die Sedimentationskraft FS ergibt sich aus der Summe von Gravitations- und Auftriebskraft, die einander entgegengerichtet sind. FS = FG + FA FS = m P g - m L g Es folgt: FS = m P g - m P Diese Sedimentationskraft FS ρ ρL g = m P g 1 - L ρP ρP bewirkt das Absinken eines Teilchens mit der dx . Anfänglich ist diese Bewegung beschleunigt, wobei dt dx mit zunehmender Geschwindigkeit die Reibungskraft FR = f proportional ansteigt. dt Sedimentationsgeschwindigkeit v = Sobald die Reibungskraft gleich der Sedimentationskraft ist, stellt sich eine gleichförmige Bewegung (Sedimentationsgeschwindigkeit) ein. f ρ dx = m P g 1 - L dt ρP Der Proportionalitätsfaktor f = 6 π η r ist der Reibungskoeffizient für kugelförmige Moleküle mit dem Radius r (Stokes). η = Viskosität des Lösungsmittels. ρ m P g 1 - L dx ρP = dt 6π η r ρ ρ P V g 1 - L = ρP 6π η r dx lässt sich also die mittlere Masse der dt Partikel ermitteln. Für das Verhalten einer Partikel im Lösungsmittel gilt daher: Aus der Sedimentationsgeschwindigkeit ρ L = ρ P FS = 0 Schweben (Gleichgewicht) ρ L < ρ P FS > 0 Sinken (Sedimentation) 229 GRÖßE UND STRUKTUR VON MOLEKÜLEN ρ L > ρ P FS < 0 Steigen (Auftrieb) Partikel sedimentieren also immer dann, wenn sie eine relativ größere Dichte besitzen als das Lösungsmittel, sie reichern sich also in Bodennähe an. Eine höhere Partikelkonzentration wird durch Diffusionsbewegungen begrenzt, so dass mit der Sedimentation nur dann Material angereichert wird, wenn die Diffusionsgeschwindigkeit v D wesentlich geringer ist als die Sedimentationsgeschwindigkeit v S. Im Schwerefeld der Erde ist dies für große Partikel wie z.B. bei der Blutsenkung der Fall, kleine Partikel können jedoch auch angereichert werden, wenn die Gravitationskraft entsprechend vergrößert wird. Zentrifugalkraft Allgemeines Ein mit konstanter Winkelgeschwindigkeit ω = dϕ dt um ein Zentrum 0 im Abstand r rotierender Körper der Masse m (Bahngeschwindigkeit v = ω r) erfährt eine zum Zentrum hin gerichtete Radial- oder Zentripetalbeschleunigung a: a =ω2 r Für einen mit dem System rotierenden Beobachter bewegt sich der Körper beschleunigt radial nach außen. Auf den Körper wirkt die radial nach außen gerichtete Zentrifugalkraft FZ: Fz = m a = m ω 2 r Zwischen der Bahngeschwindigkeit v und der Winkelgeschwindigkeit besteht folgender Zusammenhang: v =ω r für ω = konst. gilt: ω =2π ν =2π Upm 60 Upm = Umdrehungen pro Minute, ν = Umlauffrequenz 230 BIOPHYSIK DER ZELLE Trennung von Teilchen in einer Zentrifuge In einer Zentrifuge bewegt sich eine Partikelsuspension mit konstanter Winkelgeschwindigkeit auf einer Kreisbahn. Dabei wirkt auf eine Partikel der Masse mP die Zentrifugalkraft FZ : FZ = m P ω 2 r Die Partikel der Masse mP verdrängt Flüssigkeit der Masse mL. Dies bewirkt eine Auftriebskraft FA, die dem Betrag nach gleich, der Richtung nach aber entgegengesetzt der Zentrifugalkraft auf die verdrängte Flüssigkeitsmasse mL ist: FA = m L ω 2 r Die Sedimentationskraft FS ergibt sich wiederum aus der Summe von Zentrifugalkraft FZ und Auftriebskraft FA. FS = FZ + FA ρ = m P ω 2 r 1 - L ρP Unter der Wirkung der Resultierenden FZ + FA Geschwindigkeit bewegt sich die Partikel mit der dr in radialer Richtung und wird dabei durch den Reibungswiderstand der dt umgebenden Flüssigkeit abgebremst. Die Reibungskraft FR = f dr ist wiederum der dt bewegenden Kraft entgegengerichtet. Für stationäre Sedimentation lautet das Kräftegleichgewicht: FZ + FA + FR = 0 ω 2 r mP - ω 2 r mL - f ω 2 r (m P - m L ) = f dr =0 dt dr dt 231 GRÖßE UND STRUKTUR VON MOLEKÜLEN Der g-Wert Fällt ein Körper frei, d.h. wirkt auf ihn lediglich die Gravitationskraft FG, so fällt er mit der Fallbeschleunigung g, die durch die Erdanziehung hervorgerufen wird. g= FG mP In unseren geographischen Breiten ist g = 9,81 m s-2. In Zentrifugen werden durch Erhöhen der Umlauffrequenz höhere Beschleunigungswerte erreicht, wodurch schnellere Sedimentation erfolgt. Die sich ergebenden Werte bezieht man auf 'ein g' und spricht von einer Zentrifugation bei 'xg'. Beispiel: ν = 100 Umdrehungen pro Sekunde r = 0,1 m Abstand vom Drehzentrum ω = 2 π ν = 2 × 3,14 × 100 s-1 = 6,28 × 102 s-1 a = ω 2 r = 39,44 × 104 × 10-1 m s-2 = 39,44 × 103 m s-2 Das entspricht: 39 440 : 9,81 = 4020 g Die Svedberg-Konstante Theodor Svedberg, ein schwedischer Chemiker, konstruierte 1925 erstmals als Hilfsmittel für seine Untersuchungen über Kolloide eine Ultrazentrifuge. Mit ihr bestimmte er die Masse von Riesenmolekülen. Bei der Bestimmung der relativen Molekülmasse verwendet man seither eine Sedimentationskonstante (sK, Svedbergdr und der Konstante), die sich aus dem Quotienten der Absinkgeschwindigkeit dt Zentrifugalbeschleunigung ω 2 r ergibt und die die Einheit s hat: sK = 232 dr 1 dt ω 2 r BIOPHYSIK DER ZELLE Mit der Angabe der Sedimentationskonstanten charakterisiert man Moleküle oder Partikel bereits eindeutig, selbst wenn ihre Diffusionskonstante D und ihre Dichte unbekannt sind. In der Molekularbiologie haben viele der untersuchten Moleküle Sedimentationskonstanten im Bereich von 10-13 s. Man hat daher die Einheit "Svedberg" eingeführt: 1 Svedberg = 1 S = 10-13 s und charakterisiert Moleküle mit ihrem "S-Wert". Ribosomenuntereinheiten bei Prokaryonten haben S-Werte von: 30 × 10-13s sK = 30 S 50 × 10-13s sK = 50 S Beispiele: Die beiden Da die Sedimentationskonstante unter verschiedenen Bedingungen bestimmt werden kann, sind gewisse Vereinheitlichungen notwendig. Meist wird die Sedimentationskonstante auf einen Wert korrigiert, den man erhalten würde, wenn das Medium die Dichte und Viskosität von Wasser bei 20 o C hätte. Die Korrektur wird mit folgender Gleichung vorgenommen. s 20,W = s T, L η T, L (ρ P - ρ 20,W ) η 20, W (ρ P - ρ T, L ) sT,L : unkorrigierte Sedimentationskonstante in einem Medium bei der Temperatur T η T ,L : Viskosität des Mediums bei der Zeltrifugationstemperatur η 20,W : Viskosität des Wassers bei 20 o C ρP : Dichte der Teilchen in Lösung ρ T ,L : Dichte des Mediums bei Zentrifugationstemperatur ρ 20, W : Dichte des Wassers bei 20 o C Beispiele für Anwendungen der Sedimentationskonstanten (a) Bestimmung der relativen Molekülmasse Für die Masse einer Partikel ergibt sich: mP = f dr dt 1 1- 1 = f sK ρL ω r ρ 1- L ρP ρP 2 233 GRÖßE UND STRUKTUR VON MOLEKÜLEN Für kugelförmige Partikel wird der Reibungskoeffizient f = 6 π η r angeben (Stokes, 1856). In der Regel ist die Form eines Moleküls jedoch nicht bekannt. Man drückt daher den Reibungskoeffizienten f durch den experimentell bestimmbaren Diffusionskoeffizienten D aus. f = RT ND N = Lohschmidtzahl = 6,023 × 1023 mol-1 R = Allgemeine Gaskonstante T = absolute Temperatur (Kelvin) Die relative Molekülmasse Mr berechnet sich zu: M r = mP N Eingesetzt und umgeformt ergibt sich die Svedberg-Gleichung: Mr = RT D 1 ρ 1- L ρP sK (b) Bestimmung der Klärzeit Die Klärzeit ist die Zentrifugationszeit, die benötigt wird um ein Teilchen mit einem bestimmten Sedimentationskoeffizienten vollständig zu sedimentieren. Die Integration der umgeformten Gleichung in den Grenzen t1 und t2 ergibt: sK = ln r2 - ln r1 ω 2 (t 2 - t 1 ) t2 - t1 ist die Zeitdauer, die die Teilchen benötigen, um von Position r1 bis zu r2 zu gelangen. Daraus lässt sich weiterhin ableiten: t sK = ln r2 - ln r1 =K ω 2 3600 t : Zentrifugationszeit in Stunden, K : Rotorkonstante 234 BIOPHYSIK DER ZELLE Zentrifugationstechniken Differentielle Zentrifugation Die Trennung von Zellorganellen durch differentielle Zentrifugation ist eine der grundlegendsten und gebräuchlichsten Zentrifugationsverfahren. Dabei wird ein Gemisch von Partikeln (z.B. ein Zellhomogenat) stufenweise höheren Zentrifugalbeschleunigungen bei schrittweise verlängerten Zentrifugationszeiten ausgesetzt. Dabei werden die Komponenten mit großen S-Werten angereichert, während der Überstand langsamer sedimentierende Partikel mit kleineren S-Werten enthält. Die Sedimente (Pellets), die man nach jedem Zentrifugationsschritt erhält, sind jedoch stets mit langsamer sedimentierenden Komponenten verunreinigt, so dass vor einer weiteren Untersuchung das Pellet mit frischem Lösungsmittel resuspendiert und anschließend erneut zentrifugiert werden sollte. Abb. 171: Differentielle Zentrifugation (a) Vor der Zentrifugation enthält die Lösung Partikel zweier Größenklassen (b) Während der Zentrifugation wandern die größeren Partikel schneller zum Boden des Zentrifugenröhrchens (c) Ausbildung eines Pellets aus großen Partikeln, das mit kleinen Partikeln verunreinigt ist. Der Überstand ist rein und enthält nur kleine Partikel 235 GRÖßE UND STRUKTUR VON MOLEKÜLEN Abb. 172: Allgemeines Schema zur subzellulären Fraktionierung eines Säugergewebes, z.B. der Leber. Die Zahlen geben die molare Saccharosekonzentration im oberen bzw. unteren Bereich des Gradienten an. PM = Plasmamembran; SER = glattes endoplasmatisches Retikulum; RER = rauhes endoplasmatisches Retikulum; Mito = Mitochondrien Im Allgemeinen ist bei der differentiellen Zentrifugation die Verwendung eines Festwinkelrotors vorteilhafter als die eines Ausschwingrotors. 236 BIOPHYSIK DER ZELLE Abb. 173: Schnitt durch einen Festwinkelrotor In Festwinkelrotoren befinden sich die Zentrifugenröhrchen in einem festen Winkel (zwischen 14 o und 40 o ) zur Rotationsachse. Durch das Zentrifugalfeld bewegen sich die Partikel nur über kurze Distanzen in horizontaler Richtung bis sie an die Wand des Zentrifugenröhrchens stoßen. Unter geeigneten Bedingungen bildet sich an der Außenwand des Zentrifugenröhrchens ein kompaktes Pellet. Dichtegradienten-Zentrifugation Bisher wurde vorausgesetzt, dass die Sedimentation in einem homogenen Medium stattfindet. Die gleichmäßige Wanderung der Partikel in einer Ultrazentrifuge wird jedoch durch mechanische Vibrationen, Wärmegradienten und Konvektionen gestört. Diese Störungen können durch Zentrifugation in einem Dichtegradienten verringert werden. Geeignete Substanzen zur Bildung eines Gradienten sind Saccharose, Glyzerin, Cäsiumchlorid, Cäsiumsulfat und weniger gebräuchliche Stoffe wie Ficoll und Metrizamid. Der Gradient kann entweder mit einem Gradienten-Mischer vorgeformt bzw. von Hand aufgetragen werden oder bei der Zentrifugation selbst gebildet werden. Der Gradient ist am Boden des Zentrifugenröhrchens am dichtesten und nimmt mit der Höhe an Dichte ab. Die Wahl der Eigenschaften des Gradienten hängt vom gewünschten Verwendungszweck ab. Man kann die Dichtegradienten-Zentrifugation in die Zonen-Zentrifugation und die isopyknische Zentrifugation einteilen. Dichtegradienten-Differential- oder Zonenzentrifugation Das Charakteristische der Dichtegradienten-Differentialzentrifugation (rate zonal method) ist die Wanderung der Partikel durch einen stabilisierenden, sehr flachen Gradienten, dessen 237 GRÖßE UND STRUKTUR VON MOLEKÜLEN maximale Dichte nicht größer sein darf als die des am wenigsten dichten sedimentierenden Materials. Während der Zentrifugation wandern die Partikel mit einer Geschwindigkeit durch den Gradienten, die von Größe und Form der Partikel, Zentripetalbeschleunigung sowie Dichte und Viskosität des Mediums abhängt. Enthält die Probe, die auf den vorgeformten Gradienten aufgeschichtet wird, eine Mischung verschiedener Partikel, so wandert jede Partikelklasse unabhängig von den anderen durch den Gradienten und eine Trennung der Partikel kann selbst dann erzielt werden, wenn die Unterschiede in den S-Werten nur gering sind. Abb. 174: Zonen-Zentrifugation Die Zentrifugation muss also abgebrochen werden, bevor die ersten Partikel den Boden des Zentrifugenröhrchens erreicht haben. Diese Methode eignet sich gut für Substanzen, die sich zwar in der Größe, aber nicht in der Dichte voneinander unterscheiden. Zonen-Zentrifugationen werden bevorzugt in Swing-out-Rotoren durchgeführt. Swing-out-Rotoren zeichnen sich dadurch aus, dass sich die Zentrifugenröhrchen (bzw. Becher) vor der Zentrifugation in vertikaler Position befinden und während der Zentrifugation um 90 o (relativ zur Rotorachse) in die horizontale Lage ausschwenken. Im Gegensatz zu Festwinkelrotoren ist die Konvektion von Flüssigkeiten in Swingout-Rotoren herabgesetzt (d.h. Verminderung von Wandeffekten). Zudem ist der längere Weg, den die Partikel während der Sedimentation zurücklegen, vorteilhaft für die Auftrennung. Die Isolierung der Chloroplasten im Praktikumsversuch erfolgt ebenfalls nach dieser Methode. Zur Auftrennung des Materials verwendet man in diesem Fall einen diskontinuierlichen Saccharosegradienten (30%, 35%, 50%). Isopyknische Zentrifugation Die Technik der isopyknischen Zentrifugation dient der Trennung von Partikeln unterschiedlicher Dichte. Wie bei der Zonen-Zentrifugation ist ein Dichtegradient nötig, aber 238 BIOPHYSIK DER ZELLE im Unterschied dazu übersteigt hier die maximale Dichte des Gradientenmaterials die der Partikel. Zwei Typen von Dichtegradienten sind möglich: vorgeformte und solche, die sich bei der Zentrifugation unter dem Einfluss eines Zentrifugalfeldes ausbilden. In beiden Gradiententypen werden die Partikel solange wandern, bis sie in den Bereich des Gradienten gelangen, an dem die Dichte des Gradientenmaterials der Dichte der Partikel entspricht. Hier sedimentieren die Teilchen nicht weiter, da sie praktisch auf einer Unterlage schwimmen, die eine größere Dichte als sie selbst besitzt. Abb. 175: Isopyknische Zentrifugation Die so ermittelte Partikeldichte wird auch Buoyant-Dichte genannt. Buoyant-Dichten variieren entsprechend dem Medium, in dem sie bestimmt werden, da verschiedene Medien die Hydration unterschiedlich beeinflussen. In der Praxis verwendet man als Gradientenmaterial Schwermetallsalzlösungen (z.B. CsCl, Cs2SO4, KBr), die solange zentrifugiert werden, bis sich ein Sedimentations-DiffusionsGleichgewicht eingestellt hat. Gleichzeitig unterliegt auch die Verteilung der zu trennenden Moleküle einem Sedimentations-Diffusions-Gleichgewicht. Damit sich dieses Gleichgewicht einstellt, muss die Zentrifugation lange genug und mit höherer Geschwindigkeit durchgeführt werden. Nach der Auftrennung verschiedener Moleküle oder Organellen in einem Dichtegradienten schließt sich die Gradientenfraktionierung an, entweder durch Austropfen (bottom 239 GRÖßE UND STRUKTUR VON MOLEKÜLEN unloading), durch Auspumpen (top unloading) oder durch Unterschichten mit einer Flüssigkeit hoher Dichte mittels einer Pumpe wobei, das verdrängte Gradientenmaterial ein Spektralphotometer passiert, bevor es in Fraktionen gesammelt wird (upward displacement). Abb. 176: Gradientenfraktionierung:(a) Austropfen (b) Auspumpen Analytische Ultrazentrifuge Seit ihrer Entwicklung in den 30er Jahren spielte die analytische Ultrazentrifuge eine wichtige Rolle bei der Betrachtung theoretischer Aspekte der Sedimentation, der Bestimmung der Sedimentations-Konstanten und der Untersuchung von Makromolekülen. Moderne analytische Ultrazentrifugen, gekoppelt mit Computersystemen, ermöglichen darüber hinaus das Studium der molekularen und hydrodynamischen Eigenschaften von Partikeln. Das zu untersuchende Material befindet sich in Messzellen, welche nur ein geringes Fassungsvermögen von 0,4 bis 1 ml haben. Zudem besitzen sie zwei parallel angeordnete Fenster, die den Durchgang von Licht ermöglichen. Die Zellen, die insgesamt aus sehr vielen Einzelteilen bestehen, werden in den Rotor eingesetzt. Die Richtung der Sedimentation des Materials ist senkrecht zum Lichtstrahl, wobei die Verteilung der Partikel durch die Änderung der optischen Eigenschaften der Lösung festgestellt werden kann. Die für analytische Ultrazentrifugen verwendeten optischen Systeme gliedern sich in drei Typen: 1. Absorption (das zu trennende Material absorbiert Licht einer bestimmten Wellenlänge) 2. Schlierenoptische Systeme messen Änderungen im Brechungsindex des Mediums, wie sie durch Änderung der Konzentration verursacht werden 3. Interferenz 240 BIOPHYSIK DER ZELLE Abb. 177: Schlierenoptisches System einer Ultrazentrifuge 1 Lichtquelle 2 Linsen 3 Messzelle mit Fenster 4 Linsen 5 Rotor 6 Vakuumkammer Abb. 178: 7 Schlierendiaphragma 8 Kameralinsen 9 Zylindrische Linsen 10 halbdurchlässiger Spiegel 11 Bildschirm 12 Photographische Platte Schlierendiagramm während eines Sedimentations-Geschwindigkeits-Laufes 241 GRÖßE UND STRUKTUR VON MOLEKÜLEN Elektrophorese Proteine und Aminosäuren Proteine sind Polypeptidketten, die aus einer Aneinanderreihung von Aminosäuren (Primärstruktur) entstehen. Die Aminosäuren tragen immer eine Aminogruppe (NH2) und eine Carboxylgruppe (COOH) und unterscheiden sich in ihrer Seitenkette (R1). Amino- und Carboxylgruppen von aufeinanderfolgenden Aminosäuren werden durch eine Peptidbindung verknüpft. Bei dieser Verknüpfung bleibt je eine endständige NH2- und eine COOH-Gruppe erhalten. Abb. 179: Verknüpfung von Aminosäuren Ladungsverteilung in Aminosäuren bzw. Proteinen Die Amino- und Carboxylgruppen sowie die Reste R können bei unterschiedlichem pH-Wert ihre Ladung ändern. Abb. 180: Ladungsverschiebung in Aminosäuren (pIP: pH-Wert am isoelektrischen Punkt) basisches Medium saures Medium hohe H3O + -Konz. pH < pIP pH = pIP niedere H3O + -Konz. pH > pIP Die Amino- und Carboxylgruppen der Proteinenden und der Reste Rn sowie weitere protonierbare/deprotonierbare Gruppen der Reste Rn sind durch ihre Dissoziationskonstanten (pKs-Werte) charakterisiert. Entsprechend den pKs-Werten und dem aktuellen pH-Wert liegen die Gruppen protoniert beziehungsweise deprotoniert vor und tragen dadurch eine positive, negative oder gar keine Ladung. Für das elektrophoretische Verhalten ist die Summe dieser Ladungen (Nettoladung) von Bedeutung. Vereinfacht lässt sich hieraus schließen, dass die Proteine in stark saurem Milieu als Kation und in stark basischem Milieu als Anion vorliegen. 242 BIOPHYSIK DER ZELLE Abb. 181: Beweglichkeiten von Aminosäuren bei unterschiedlichen pH-Werten Elektrophoretische Trennmethoden für Proteine Die folgenden Trennmethoden werden ausschließlich für Proteine verwendet. Die gängigen Methoden nutzen das unterschiedliche Molekulargewicht bzw. die Aminosäurezusammensetzung dieser Makromoleküle aus. Man trennt also: - nach Molekulargewicht: SDS-Gel-Elektrophorese - nach Ladung: isoelektrischer Fokussierung (IEF) - nach Ladung und Molekulargewicht: 2D-Gel-Elektrophorese SDS-Gel-Elektrophorese Um die Proteine ausschließlich nach ihrem Molekulargewicht zu trennen, werden sie in einem (Laemmli-)Probenpuffer mit dem Detergenz SDS (sodium dodecyl sulfate) und dem Reduktionsmittel 2-Mercaptoethanol aufgenommen. SDS bewirkt die Solubilisierung und stark negative Aufladung der Proteine, so dass sie sich im elektrischen Feld bezüglich ihrer Gesamtladung gleich verhalten. Mercaptoethanol bewirkt durch die Reduktion von Schwefelbrücken zu Sulfhydrylgruppen eine Zerstörung der Quartär- und Tertiärstruktur und damit eine ausschließliche Trennung nach dem Molekulargewicht und nicht nach der räumlichen Struktur. Die Proben werden nach Aufnahme in Laemmli-Probenpuffer im elektrischen Feld in 5% Sammelgel konzentriert, um dann in 12,5%igem Trenngel aufgetrennt zu werden. Nach Beendigung der Gel-Elektrophorese werden die Proteinbanden in einer Coomassie Blau R250-Lösung fixiert und gefärbt. Mit Hilfe von Eichproteinen lassen sich den Proteinbanden die entsprechenden Molekulargewichte zuordnen. Isoelelektrische Fokussierung (IEF) Die Auftrennung von Proteinen nach ihrem Anteil an sauren und basischen Resten geschieht mit der isoelektrischen Fokussierung. Durch Gel-Elektrophorese eines Gemisches von Polyampholyten wird zunächst ein pH-Gradient hergestellt. In diesem werden die Proteinproben anschließend elektrophoretisch aufgetrennt. Die Proteine werden hierbei an 243 GRÖßE UND STRUKTUR VON MOLEKÜLEN dem pH-Wert nicht mehr weiterwandern, an dem ihre Nettoladung Null wird, das heißt die Ladungen der NH2- und COOH-Gruppen sowie der in den Resten R vorhandenen anderen Gruppen ausgeglichen sind. Dieser Punkt wird als isoelektrischer Punkt bezeichnet. 2D-Gel-Elektrophorese Die 2D-Gel-Elektrophorese ist eine Kombination der IEF und SDS-Gel-Elektrophorese zur Auftrennung der Proteine nach ihrem isoelektrischen Punkt und Molekulargewicht. Zunächst werden sie mittels der IEF in einem Gelröhrchen aufgetrennt. Anschließend wird dieses auf ein SDS-Gel überführt und die Auftrennung nach dem Molekulargewicht durchgeführt. Der Nachweis der Proteine kann ebenfalls durch Coomassie Blau-Färbung erfolgen. Proteinbestandteile am Beispiel des Serums Proteinfraktion Mr IP beiAnteil Bedeutung pH % Reserve-Eiweiß Albumine 61-69 k 4,9 60 a1-Globuline a2-Globuline b-Globuline 44-200 k 5,1 160-820 k 5,4 3-20 k 5,8 4 7 12 g-Globuline 150-960 k 7,3 17 kolloidosmot. Druck Lipidtransport Oxidaseaktivität Lipidtransport Antikörper Immunglobuline M r = relative Molekülmasse, Ip = isoelektrischer Punkt Tabelle: Serumproteine Das Blut macht etwa 6 - 8% des Körpergewichtes aus. Es dient neben dem respiratorischen Gastransport auch dem Transport von Nährstoffen, Exkreten, Hormonen, Vitaminen, Enzymen, Elektrolyten und immunogenen Zellen. Es ist für die Wasser- und Temperaturregulation im Körper ebenso wichtig wie für die Pufferung der Körperflüssigkeiten. Aus der Blutflüssigkeit (Blutplasma) können die Zellen durch Zentrifugation und das Fibrinogen durch Gerinnung abgetrennt werden, so dass Blutserum übrig bleibt. Im Serum sind viele essentielle Substanzen enthalten, wie Kohlehydrate, Fette, Ionen und Proteine. Serum wird Zellkulturen als wachstumsstimulierende Komponente zugegeben. 244 BIOPHYSIK DER ZELLE Nukleinsäuren Nukleinsäuren sind fadenförmige Polymere, die aus einem Zucker-Phosphat-Rückgrat und daran gebundenen Stickstoffbasen bestehen (siehe Abb. 182). Ein Monomer, bestehend aus einem Zucker, einem Phosphorsäurerest und einer Stickstoffbase wird als "Base" bezeichnet. Kette Desoxyribonukleotiden Abb. 182: von vier Liegen die Nukleinsäuren als Doppelhelix vor, so ergeben zwei gegenüberliegende Monomere ein Basenpaar (bp). Ein DNA-Molekül mit einer Länge von 1000 Basen ist dann eine Kilobase (kb) Nukleinsäuren. DNA und RNA sind unter physiologischen Bedingungen immer negativ geladen. Extrem hohe pH-Werte spalten das Rückgrat der Nukleinsäuren. Ihre Ladung wird durch die Phosphorsäurereste des Rückgrats geprägt, wobei jeder Rest eine negative Ladung trägt. Zu niedrige pH-Werte führen zu einer Absättigung der negativen Phosphatgruppen. Die Folge ist die Unbeweglichkeit und Ausfällung der Nukleinsäuren in einem Elektrolyten. Elektrophoretische Trennmethoden für Nukleinsäuren Die Methode für die Nukleinsäureauftrennung richtet sich nach der Größe der Moleküle und dem angestrebten Auflösungsvermögen. Die am häufigsten verwendeten drei Methoden sind: 245 GRÖßE UND STRUKTUR VON MOLEKÜLEN • das Agarose-Gel mit der "Submarine"-Technik • das Agarose-Gel im "Pulsed Field"-Verfahren • das hochauflösende Polyacrylamid-Gel Agarose-Gel mit der "Submarine"-Technik Diese Methode ist die Standardmethode zur Trennung, Reinigung und Identifizierung von Nukleinsäuren. Bei der "Submarine"-Technik befindet sich das Agarose-Gel in horizontaler Lage und ist völlig mit dem Elektrophoresepuffer bedeckt. Dadurch wird das Gel vor dem Austrocknen geschützt. Die Sichtbarmachung der Nukleinsäuren erfolgt über die Anfärbung mit Ethidiumbromid. Dieses planare Molekül schiebt sich zwischen zwei Basen und verstärkt damit sein Fluoreszenzverhalten unter UV-Anregung, so dass die angefärbten Molekülbanden sichtbar werden. "Pulsed-Field" Agarose-Gel-Elektrophorese Diese modifizierte "Submarine"-Technik wird zur Trennung von sehr großen Nukleinsäuremolekülen (meist Chromosomen) eingesetzt. Nukleinsäuremoleküle mit einer Größe von über 20 kb richten sich in der herkömmlichen Agaroseelektrophorese der Länge nach aus und wandern im elektrischen Feld mit gleichen Geschwindigkeiten. In der "PulsedField" Gel-Elektrophorese (PFG) ändert sich nun die Richtung des elektrischen Gleichstromfeldes periodisch. Dadurch sind die Moleküle gezwungen, ihre Ausrichtung ständig zu ändern. Kürzere Nukleinsäurestränge vollziehen diesen Prozess schneller, weshalb sie dann auch eine höhere Beweglichkeit besitzen. Hochauflösendes denaturierendes Polyacrylamid-Gel Im Gegensatz zur PFG ist diese Methode besonders zur Auflösung von sehr kleinen Unterschieden in der Größe der Moleküle geeignet. Das restriktive Polyacrylamid-Gel ist vertikal angeordnet und enthält zudem noch hohe Harnstoffkonzentrationen. In Verbindung mit einer zusätzlichen externen Erwärmung, bewirkt das eine Denaturierung der Doppelstränge. Das hohe Auflösungsvermögen von Polyacrylamid-Gelen ermöglicht dann eine Auftrennung von Molekülen, deren Längenunterschied nur eine Base beträgt. Deshalb wird diese Technik meistens zur Sequenzierung oder zur Identifikation von Punktmutationen eingesetzt. Grundlagen der Trennmethode Elektrolyte, Ionen, Elektrolyse Elektrolyte sind Stoffe, deren Moleküle in einem Lösungsmittel zu Ionen dissoziieren können. Eine Elektrolytlösung kann daher einen elektrischen Strom leiten. Taucht man Drähte oder 246 BIOPHYSIK DER ZELLE Platten ("Elektroden") aus Metall (z.B. Platin, Silber) in eine Elektrolytlösung ein, so fließt beim Anlegen einer Gleichspannung U ein elektrischer Strom I. Dieser Ladungstransport kommt dadurch zustande, dass in der wässrigen Lösung positive Ionen (Kationen) zur einen Elektrode (Kathode), negative Ionen (Anionen) zur anderen Elektrode (Anode) wandern. Im Gegensatz zu dieser "Ionenwanderung" besteht im Innern der Metallelektroden der Ladungstransport aus einer Wanderung von Elektronen (e-). An der Grenzfläche Elektrode/Lösung findet also ein Übergang von einem "elektronischen" zu einem "ionischen" Leitungsmechanismus statt. Dieser ist mit einer chemischen Reaktion an den Elektroden ("Elektrolyse") verbunden. Kathode: 2 H + (Lösung) + 2 e- (Metall) → H 2 (gasförmig) Anode: 2 Cl − (Lösung) → 2 e − (Metall) + Cl 2 (gasförmig) Elektrisches Feld; elektrische Kraft; elektrische Arbeit und Leistung Legt man an zwei Elektroden im Abstand d eine Spannung U, so erzeugt diese in einer Elektrolytlösung ein elektrisches Feld mit der elektrischen Feldstärke E E= U d Die elektrische Feldstärke E ist stets vom Pluspol zum Minuspol gerichtet. Auf eine positive Ladung q wirkt dann eine elektrische Kraft FE FE = q E in Richtung der Feldstärke, so dass sich ein positiv geladenes Teilchen in Richtung der Kathode bewegt. Ein negativ geladenes Teilchen bewegt sich zur Anode. Die entgegengesetzt geladenen Ionenwolken der Teilchen wandern stets in die entgegengesetzten Richtungen. Geschwindigkeit, Beweglichkeit der Teilchen Infolge der an den geladenen Teilchen oder Molekülen angreifenden elektrischen Kraft erfährt das Teilchen eine beschleunigte Bewegung. Die Geschwindigkeit steigt so lange, bis die dadurch ebenfalls größer werdende Reibungskraft des Teilchens genauso groß geworden ist wie die antreibende elektrische Kraft FE. Diese Reibungskraft wird für kugelförmige Teilchen durch das Stokessche Gesetz beschrieben: FE = q E = 6 π η r v 247 GRÖßE UND STRUKTUR VON MOLEKÜLEN η = dynamische Viskosität des Lösungsmittels r = wirksamer Radius incl. Hydrathülle v = Geschwindigkeit Im Gleichgewicht der Kräfte bewegt sich das Teilchen mit gleichbleibender Geschwindigkeit v weiter: v= qE 6π η r Die Geschwindigkeit v ist proportional der angelegten Spannung U, alle anderen Größen sind dagegen Materialkonstanten des interessierenden Teilchens bzw. Moleküls. Deshalb gibt man als charakteristische Größe für das Teilchen oder Molekül die auf die elektrische Feldstärke E bezogene Geschwindigkeit an. Dies ist die Beweglichkeit u: u= v E Man kann die Beweglichkeit eines Moleküls also durch die Messung der Wanderungsgeschwindigkeit v und der vorgegebenen elektrischen Feldstärke E bestimmen. Abb. 183: Elektrophorese Schema einer trägerfreien Elektrophorese Die Wanderung geladener Moleküle im elektrischen Gleichstromfeld (siehe Abb. 183) nennt man Elektrophorese. Aufgrund unterschiedlicher Ladung und Masse bewegen sie sich mit unterschiedlichen Geschwindigkeiten. Meistens wird die relative Beweglichkeit einer Substanz zu einem mitaufgetrennten Standard angegeben. Dadurch lassen sich nicht nur Stoffe auftrennen, sondern auch durch ihr Wanderungs-Verhalten charakterisieren. Man unterscheidet drei grundsätzlich verschiedene elektrophoretische Trennmethoden: 248 BIOPHYSIK DER ZELLE • Zonen-Elektrophorese (eigentliche Elektrophorese): Homogenes Puffersystem mit stabilem pH-Wert. Auftrennung nach Masse, Gestalt und Ladung. Das Maß für die elektrophoretische Beweglichkeit wird anhand der zurückgelegten Strecke in einer bestimmten Zeit gemessen. • Isoelektrische Fokussierung (kurz IEF): Ein permanenter pH-Gradient entlang des elektrischen Feldes verursacht bei amphoteren Substanzen eine Änderung der Ladung während des Durchwanderns des Gradienten. Das hat zur Folge, dass die Substanz bei einem bestimmten pH-Wert eine Nettoladung von Null aufweist und damit nicht mehr im elektrischen Feld wandert. Die Substanz wird an dieser Stelle fokussiert. • Isotachophorese (kurz ITP): Hier sorgt ein diskontinuierliches, mitwanderndes Puffersystem mit einem schnellen Leitionenelektrolyt und einem langsamen Folgeionenelektrolyt für eine stapelförmige Anordnung nach der elektrophoretischen Mobilität der Substanzen. Diese Methode wird hauptsächlich in der quantitativen Analyse eingesetzt. Man unterscheidet elektrophoretische Trennmethoden in freier Lösung (WanderndeGrenzschichten-Elektrophorese, kontinuierliche trägerfreie Elektrophorese, Kapillarelektrophorese) von der Auftrennung in stabilisierenden Medien (Agarose-Gel, Polyacrylamid-Gel). Puffersysteme Der pH-Bereich und die Ionenstärke sind die wichtigsten Merkmale eines Puffers und sind der Probenart anzupassen. Der pH-Wert sollte während der Elektrophorese stabil bleiben und den pH-Wert der Proben überdecken. Da die Pufferionen im elektrischen Feld ebenfalls mitwandern, müssen ausreichend große Puffervorräte vorhanden sein. Die Ionenstärke sollte bei stabiler Pufferkapazität gerade so hoch liegen, dass die zur Trennung benötigte Leistung möglichst gering ausfällt. Höhere Leistung führt zu einer Erwärmung des Trägermaterials und der Probe, was zu Veränderungen im Verhalten führen kann. Trennmedien Die Wahl eines Trennmediums richtet sich nach der Art der zu untersuchenden Substanz. Die Medien müssen chemisch inert sein, ihre Struktur sollte weitgehend homogen und hitzestabil sein und ihr Vernetzungsgrad muss reproduzierbar eingestellt werden können. Die in der Biologie am häufigsten verwendeten polymeren Trägermaterialien sind die Agarose und das Polyacrylamid. 249 GRÖßE UND STRUKTUR VON MOLEKÜLEN Polyacrylamid-Gele Polyacrylamid-Gele erhält man durch Polymerisation von Acrylamid mit dem quervernetzenden N,N'-Methylendiacrylamid. Zum Starten der Reaktion wird ein Radikalstarter benötigt. Der Vernetzungsgrad wird durch die Konzentration der quervernetzenden Substanz eingestellt und ist in hohem Maße reproduzierbar. Die geringe Porengröße des Gels verhindert die Diffusion der Probenmoleküle und ermöglicht eine sehr genaue Auftrennung. Solche Gele werden auch als restriktive Gele bezeichnet. Vor Reaktionsbeginn sind die Gelbestandteile giftig. Der Prozess ist nicht reversibel, eine Rückgewinnung von Substanzen aus dem Gel ist daher schwierig. Die Konzentration (=Vernetzungsgrad) c des Gels lässt sich mit folgender Formel berechnen: c= b 100 [ %] a+b a = Masse Acrylamid in g, b = Masse Methylendiacrylamid in g Abb. 184: Polymerisation von Acrylamid und Methylendiacrylamid 250 BIOPHYSIK DER ZELLE Agarose-Gele Agarose ist ein Polysaccharid (siehe Abb. 185), das aus roten Meeresalgen gewonnen wird. Abb. 185: Agarose Es wird in Elektrophoresepuffer aufgenommen und dann durch Erhitzen in Lösung gebracht. Die vielen Hydroxy-Gruppen (R-OH) ermöglichen die Ausbildung von WasserstoffbrückenBindungen, wodurch die großporige Gelmatrix ihre Festigkeit erhält. 251 GRÖßE UND STRUKTUR VON MOLEKÜLEN Abb. 186: Ausbildung der Gelstruktur eines Agarose-Gels Während des Abkühlens lagern sich Doppelhelices parallel aneinander und binden dann an andere Helices. Agarose-Gele sind großporige so genannte nicht restriktive Gele, bei denen die Molekülgröße eine geringere Rolle spielt. Mit ihnen wird allein nach Ladung getrennt. Der Nachteil ist ein geringeres Auflösungsvermögen, da die Diffusion nicht unterbunden wird. Vorteile der Agarose sind die einfache Herstellung und die Möglichkeit, nach Auftrennung aus dem Gel Stücke mit angereicherter Substanz herauszuschneiden. Aus diesen Stücken kann man dann durch Erhitzen die Substanzen leicht freisetzen. Röntgenstrukturanalyse Röntgenstrahlung ist eine Form der elektromagnetischen Strahlung mit einer typischen Wellenlänge von ca. 0,1 nm (= der Durchmesser eines H-Atoms). Lenkt man Röntgenstrahlung auf eine kristalline Substanz, so wird ein Teil der Strahlung gestreut. Die gestreuten Wellen werden sich an bestimmten Stellen verstärken und auf einem speziellen Detektor als Beugungsflecken erscheinen. Diese Flecken in einem bestimmten 252 BIOPHYSIK DER ZELLE Röntgenbeugungsmuster geben Informationen über die Lage der Atome im Kristall. Die Analyse der Röntgenbeugungsanalyse ist heute weitgehend automatisiert. Aus der Aminosäure-Sequenz eines Proteins lässt sich in der Regel die dreidimensionale Struktur nicht voraussagen. Durch Kristallisieren von Proteinen ist es gelungen, auch die räumliche Gestalt von Proteinen aufzuklären. Allerdings gibt es viele Proteine, die noch nicht kristallisiert werden konnten. Abb. 187: Schema einer Röntgenbeugungsapparatur (aus: H. Lodish, A. Berk, S.L. Zipursky, P. Matsudaira, D. Baltimore, J. Darnell: "Molecular Cell Biology" Scientific American Books, New York, 1999) 253 GRÖßE UND STRUKTUR VON MOLEKÜLEN Abb. 188: Beugungsdiagramm (aus: H. Lodish, A. Berk, S.L. Zipursky, P. Matsudaira, D. Baltimore, J. Darnell: "Molecular Cell Biology" Scientific American Books, New York, 1999) Kernresonanzspektroskopie (NMR) Die Kernresonanzspektroskopie dient der Strukturaufklärung kleiner Moleküle. Der Vorteil der NMR gegenüber der Röntgenstrukturanalyse liegt darin, dass keine kristalline Probe benötigt wird. Man braucht nur ein kleines Volumen konzentrierter Probenlösung. Diese wird in ein starkes Magnetfeld gebracht. Einige Atomkerne (z.B. die der Wasserstoffatome) haben ein magnetisches Moment (Spin). Dieser Spin richtet sich in einem magnetischen Feld parallel zu diesem aus. Mit Hilfe von Pulsen elektromagnetischer Strahlung im Radiowellenbereich kann man den Spin in einen nicht-parallelen Zustand versetzen. Kehrt das magnetische Moment in den parallelen Zustand zurück, emittieren die angeregten Wasserstoffkerne Strahlung mit Radiowellenfrequenz. Die Frequenz und Intensität dieser emittierten Strahlung hängen von der Umgebung der Wasserstoffatome ab; je nachdem, ob die Kerne in der Umgebung angeregt sind oder nicht. Eine Weiterentwicklung dieser Technik – die zweidimensionale NMR – ermöglicht es, die Signale der Wasserstoffkerne in unterschiedlichen Aminosäureresten zu unterscheiden und zu identifizieren. Auch Rückschlüsse auf die Entfernung zwischen Wasserstoffatomen können gezogen werden. Damit kann dann schließlich die dreidimensionale Struktur eines Moleküls dargestellt werden. In vielen biologisch wichtigen Molekülen ist Phosphat enthalten (ATP, DNA, Phospholipide), daher wird in Medizin und Biologie häufig die 31P-NMR-Spektroskopie eingesetzt. Dies ist eine nicht-invasive Untersuchungsmethode für physiologische Parameter in lebendem Gewebe, die als NMR-Tomographie dargestellt werden. 254 BIOPHYSIK DER ZELLE Strömung und Viskosität Strömung Im Allgemeinen sind Flüssigkeiten inkompressibel, d.h. sie haben eine konstante Dichte ρ , unabhängig von dem auf sie wirkenden Druck. Strömt nun eine Flüssigkeit durch ein Rohr, das nicht überall denselben Durchmesser hat, so kann man beobachten, dass die Strömungsgeschwindigkeit nicht überall im Rohr konstant ist: Abb. 189: Abhängigkeit der Fliessgeschwindigkeit vom Rohrquerschnitt Man misst hier drei verschiedene Geschwindigkeiten, die scheinbar abhängig von dem Radius des Rohres sind. Die Stromdichte ergibt sich hier aus: r j = nν ν = Geschwindigkeitsfeld n = Teilchendichte Und damit ergibt sich für den Teilchenstrom: I= j A A = Rohrquerschnitt Der Teilchenstrom ist also abhängig von dem Rohrquerschnitt und nimmt mit zunehmender Fläche ab. Dies wird auch deutlich, wenn man die Massenerhaltung beachtet. Diese besagt, das weder Masse verloren geht, noch neu entsteht, es muss also dieselbe Masse aus dem Rohr rausfließen, wie reingeflossen ist. Da Flüssigkeiten inkompressibel sind, gilt dies auch für die Volumina. Ist dies aber der Fall, dann muss bei einem engeren Rohrquerschnitt die Flüssigkeit schneller strömen, um in derselben Zeit das gleiche Gesamtvolumen zu transportieren, die Flüssigkeit wird also an der Stelle der Verengung beschleunigt. Das Verhältnis der Geschwindigkeiten entspricht dem Verhältnis der Querschnittsflächen: 255 GRÖßE UND STRUKTUR VON MOLEKÜLEN ν2 = A1 ν1 A2 Diese Gleichung nennt man auch Kontinuitätsgleichung. Betrachtet man nun die Drücke im Rohr, so kann man beobachten, dass der Druck umso kleiner ist, je weiter das Rohr ist. Der Druck berechnet sich ganz allgemein aus: p= F ⇒F=pA A Betrachten wir zunächst ein Rohr, das sich nach rechts verengt. Links ist ein Kolben angebracht. Durch eine Bewegung des Kolbens mit der Kraft F1 in das Rohr hinein wird eine Strömung erzeugt. Es wirkt also ein Druck p1. Nun kann man die Arbeit berechnen, die beim Drücken des Kolbens verrichtet wird: W1 = p1 A1 ν 1 ∆t Befindet sich an der rechten Seite des Rohrs ebenfalls ein Kolben, dann wird dieser aus dem Rohr heraus gedrückt. Dabei wird ebenfalls Arbeit verrichtet: W2 = p 2 A 2 ν 2 ∆t Man kann nun beobachten, dass der Druck p1 > p2 ist. Da A × ν = konst. ist (Kontinuitätsgleichung), ist W2 < W1. Es gilt aber außerdem der Energieerhaltungssatz, d.h. die Summe der verrichteten Arbeiten muss 0 sein. Die Differenz zwischen W1 und W2 ist genau die Arbeit die benötigt wird, um die Flüssigkeit an der Verengung zu beschleunigen. Außerdem gilt, dass die Summe aller Kräfte 0 ist: ( ) Flin ker Kolben − Frechter Kolben + FVerengung = 0 Ersetzt man hier die Kräfte durch die Drücke, so erhält man: p links p rechts = + FVerengung A links A rechts Hier sieht man deutlich, dass der Druck prechts < plinks. Betrachten wir nun noch die kinetische Energie eines Volumenelements: Wkin = 256 1 ρ A1 ν 1 ∆tν 12 2 BIOPHYSIK DER ZELLE Alle Größen außer der Geschwindigkeit sind konstant. Da die Geschwindigkeit nach der Verengung größer geworden ist, nimmt auch die kinetische Energie zu. Die Differenz zwischen den kinetische Energien entspricht genau der Differenz der Schubarbeit am linken und am rechten Kolben. Die Summe aller Arbeiten ist also 0 (Energieerhaltung). Aus dieser Betrachtung folgt die Bernoulli Gleichung: p1 + 1 1 ρ ν 12 = p 2 + ρ ν 22 = konst. 2 2 Strömungen in Form des Blutkreislaufs spielen bei Tieren und Menschen eine lebenswichtige Rolle. Das Blut verlässt das Herz durch die Aorta, und verzweigt sich anschließend in Arterien bis hin zu den feinen Kapillaren (z.B. in der Lunge). Dabei nimmt der Gesamtquerschnitt und somit auch die Gesamtfläche stark zu. In der Aorta des Menschen strömt das Blut mit einer Geschwindigkeit von ca. 100 mm/s. Aufgrund der Flächenvergrößerung nimmt die Geschwindigkeit bis auf 1 mm/s in den Kapillaren ab. Anschließend münden die Kapillaren wieder in die Venen, die Geschwindigkeit nimmt wieder zu. Viskosität Betrachten wir zwei durch Flüssigkeit getrennte Platten, die sich relativ zueinander bewegen: Abb. 190: Kraftwirkung auf zwei bewegte Platten in einer viskosen Flüssigkeit. Die Viskosität η der Flüssigkeit ist konstant. Die Molekülschicht der Flüssigkeit, die direkt an die obere Platte angrenzt, bewegt sich mit der selben Geschwindigkeit wie die Platte, die Molekülschicht, die direkt an die untere Platte angrenzt, bewegt sich mit der Geschwindigkeit der unteren Platte. Beides hat etwas mit der Wechselwirkung der Moleküle der Flüssigkeit und der Platte zu tun, und in beiden Fällen wird ein Teil dieser Bewegungsenergie an die nächste Schicht weitergegeben. Geht man nun von der oberen bewegten Platte in Richtung der unteren langsameren Platte, so kann man beobachten, dass die Geschwindigkeit langsam abnimmt, weil der Einfluss der schnell bewegten Platte auf die Moleküle immer stärker ab-, und der Einfluss der langsam bewegten Platte immer stärker zunimmt. Der Geschwindigkeitsverlauf ist linear. Man bezeichnet eine solche Strömung auch als laminare Strömung, weil die Molekülschichten parallel strömen, es findet keine Bewegung in vertikaler 257 GRÖßE UND STRUKTUR VON MOLEKÜLEN Richtung statt, es wirken lediglich Kräfte zwischen den Schichten. Im Gegensatz dazu gibt es Strömungen, bei denen dies nicht der Fall ist, sie werden als turbulente Strömungen bezeichnet. Hier treten Verwirbelungen der Molekülschichten auf, eine genauere Betrachtung erfolgt weiter unten. Betrachtet man eine laminare Strömung zwischen zwei ruhenden planparallelen Platten, so ist auch hier die Strömungsgeschwindigkeit nicht an jeder Stelle gleich: Abb. 191: Geschwindigkeitsverteilung in einem Rohr. Die Viskosität der Flüssigkeit sei auch hier konstant. Da aber die Strömungsgeschwindigkeit zur Mitte zunimmt, entsteht ein Druckgefälle von außen nach innen. Bei z = + d oder z = - d ist die Geschwindigkeit der Moleküle 0. Die Moleküle haften an den Platten. Die nächste Molekülschicht bewegt sich bereits langsam, sie wird jedoch von er vorherigen Schicht durch die Wechselwirkungen gebremst. Genau zwischen den zwei Platten ist die Entfernung zu den „stehenden" Molekülschichten am größten, und damit die Geschwindigkeit am größten. Die Form der Parabel des Geschwindigkeitsverlaufes ist abhängig von der Viskosität. Steigt die Viskosität, so steigen auch die Wechselwirkungen der Molekülschichten, und die Geschwindigkeit nimmt von einer Schicht zur nächsten um einen großen Wert zu. Die Parabel wird relativ spitz. Lässt man z.B. eine schleimige Substanz zwischen zwei Platten laufen, so erreicht diese keine hohe Strömungsgeschwindigkeit, aber der Geschwindigkeitsgradient wird sehr groß, Wasser dagegen fließt fast ungebremst. Idealisiert man die Strömung und geht davon aus, das sich alle Moleküle unabhängig von ihrer Lage zwischen den Platten mit der gleichen Geschwindigkeit bewegen, so spricht man von einer Kolbenströmung. Zwischen zwei ruhenden planparallelen Platten ist die Geschwindigkeit eine parabelförmige Funktion von z. Betrachtet man ein Volumenelement aus der strömenden Flüssigkeit, so wirken hier tangentiale Reibungskräfte Fx. Diese Reibungskräfte greifen auf einer Fläche: A=bl an. Daraus ergibt sich ein Druck: px = 258 F F = A bl BIOPHYSIK DER ZELLE Der Druck px ist aber nicht an allen Stellen entlang der z-Achse gleich, denn er hängt wiederum von der Strömungsgeschwindigkeit und der Viskosität ab: p x = -η dν z dz Je größer die Viskosität, desto größer die Druckdifferenz zwischen den Schichten. Das negative Vorzeichen ergibt sich aus der Lage des 0 Punktes, entscheidend sind die Druckdifferenzen, die unabhängig vom absoluten Druck und damit vom Vorzeichen sind. Kapillar-Viskosimeter Abb. 192: Kapillar-Viskosimeter. Dieses Gerät dient der Bestimmung von Viskositäten. Die zu messende Flüssigkeit wird in den oberen Behälter eingefüllt und das Volumen gemessen, das in einer bestimmten Zeit vom oberen Behälter in den unteren fließt. Je höher die Viskosität ist, desto langsamer fließt die Flüssigkeit. Betrachtet wir zunächst nur das Rohr: 259 GRÖßE UND STRUKTUR VON MOLEKÜLEN Abb. 193 Gehen wir davon aus, die Flüssigkeit in der Kapillare würde sich mit geringer Geschwindigkeit bewegen, dann ist die Reibungskraft der Antriebskraft entgegengesetzt: dν = pπ r2 dr p - dν = r dr 2η l −η 2 π r l ν= R (R r dr = 2η l ∫ 4η l p p 2 − r2 ) 0 2 π r l = Innen-Umfang der Kapillare Da die Strömungsgeschwindigkeit im Rohr nicht gleich ist (am Rand ist sie 0, in der Rohrmitte ist sie maximal, ähnlich wie bei zwei Platten), eignet sie sich nicht als Messgröße. Deshalb ist es einfacher, das Volumen als Messgröße zu verwenden: R dV = (2 π r )ν dr dt ∫0 setzt man die Gleichung für ν ein, ergibt sich: πp 3 πp 4 −p 2 dV = ∫ (2 π r ) r dr = − r dr = R ∫ dt 0 4η l 8η l 0 8η l R R Der Druck p ergibt sich aus der Höhe h, die konstant ist, wenn die beiden Volumina der Gefäße gleich sind. Man misst nun die Zeit, die der Meniskus benötigt, um von „0" zu „1" zu kommen. Mit Hilfe der Zeit lässt sich nun die Viskosität bestimmen, indem man die Gleichung nach η auflöst. 260 BIOPHYSIK DER ZELLE Viskosimeter Abb. 194: Rotationsviskosimeter. Rotationsviskosimeter: Die zu messende Flüssigkeit wird in einen Stahlzylinder eingefüllt und ein zweiter Stahlzylinder wird so in die Flüssigkeit getaucht, dass nur ein Spalt von einigen Millimetern zwischen den beiden Zylindern bleibt und sie sich an keiner Stelle berühren. Dreht sich der äußere Zylinder, so wird der innere Zylinder mitgenommen, was zu einem Drehmoment führt, das man messen kann. Je größer die Viskosität der Flüssigkeit im Zwischenraum der beiden Zylinder, desto höher das Drehmoment, das auf den inneren Zylinder wirkt, denn die Kraftübertragung zwischen den einzelnen Molekülschichten ist in diesem Fall sehr groß. Eine Messreihe besteht oft aus verschiedenen Drehgeschwindigkeiten des äußeren Zylinders, denn die Viskosität kann sich mit der Rotationsgeschwindigkeit ändern. In einem solchen Fall erhält man eine nicht lineare Funktion wenn man die Geschwindigkeit gegen die Schubspannung (Kraft zwischen zwei Molekülschichten in der Flüssigkeit) bzw. gegen das Drehmoment aufträgt. 261 GRÖßE UND STRUKTUR VON MOLEKÜLEN Abb. 195 Die rote Kurve zeigt den Verlauf der Messung einer Nukleinsäure-Lösung. Hier nimmt die Schubspannung nicht linear mit der Drehgeschwindigkeit zu. Die Viskosität ist also nicht konstant. Die grüne Kurve zeigt den Verlauf der Messung von Wasser (Newtonsche Flüssigkeit). Die Viskosität ist konstant. relative Viskosität: η rel = η η0 reduzierte Viskosität: η red = η - η0 η0 Viskositätszahl: Is = Grenzviskosität: I 0 = lim I s 1 η - η0 c η0 c,s → 0 Beispiele: Viskosität Luft, Gas Wasser Öle Bitumen 0,01-0,02 mPa s 1 mPa s 150-800 mPa s 105 mPa s Denaturierung und Viskosität Misst man die relative Viskosität einer DNA Lösung mit steigender Temperatur, dann erhält man folgenden Verlauf: 262 BIOPHYSIK DER ZELLE Abb. 196: Viskositätsverlauf beim Schmelzen von DNA in Lösung. Die Denaturierung setzt bei einem charakteristischen Wert, dem TM – Wert ein (temperature of melting). Kurz vor dieser Temperatur beginnt die Viskosität der Lösung schlagartig abzunehmen. Erst wenn die DNA vollständig denaturiert ist, nähert sich die Viskosität wieder einem konstanten Wert. Zusammenhang zwischen Viskosität und relativer Molekülmasse Die Gleichung, die diesen Zusammenhang beschreibt, wurde empirisch aus Messergebnissen ermittelt: η = K A ar K und a sind Konstanten, die vom Molekül und vom Lösungsmittel abhängen. Blutsenkung Mit Hilfe der Blutsenkung können Infektionen nachgewiesen werden. Hierzu wird eine Blutprobe des Patienten genommen. Lässt man diese einige Zeit stehen, so sedimentieren die Blutzellen, d. h. überwiegend Erythrozyten. Beim Blut eines gesunden Menschen sinken diese mit einer Geschwindigkeit von 3-8 mm/h. Männer haben einen Hämatokrit-Wert von ca. 45%, Frauen von ca. 40%. Der Hämatokrit-Wert beschreibt das Verhältnis von Blutzellen zum gesamten Volumen. Bei einer Infektion können Plasmaeiweiße an die Erythrozyten angelagert sein, wodurch die Sinkgeschwindigkeit abnimmt. Man kann die Sinkgeschwindigkeit mit dem Stoke’sche Gesetz berechnen: 2 R2 g (ρ − ρ fl ) νs = 9 η 263 GRÖßE UND STRUKTUR VON MOLEKÜLEN Erythrozyten sind zwar normalerweise scheibenförmig abgeflacht (7,5 mm Durchmesser, 1,5 mm Dicke), man kann sie aber als grobe Näherung als Kugeln mit dem gleichen Volumen annehmen (Radius 2,75 mm). Setzt man nun noch die Dichten der Erythrozyten und der Flüssigkeit sowie die Viskosität des Blutplasmas (1,73 mPa × s) ein, so erhält man einen Wert von ungefähr 2,4 mm/h. Sind Plasmaeiweiße an die Erythrozyten gebunden, so nimmt der Radius zu und die Sinkgeschwindigkeit ab. Man kann die Sinkgeschwindigkeit des Blutes durch Entfernen des Calciums im Blut verändern, da dadurch die Blutgerinnung verhindert wird. Die Blutzellen setzen sich daher leichter ab. Ändert sich das Verhältnis von Albumin zu Globulin, nimmt die Viskosität des Plasmas ebenfalls ab. Bei Erhöhung der Agglomerine im Blut, aggregieren vermehrt Erythrozyten und sinken ebenfalls schneller ab. Strömungswiderstand Der Strömungswiderstand FW ist die Kraft, die auf einen Gegenstand wirkt, wenn dieser von einer Flüssigkeit umströmt wird. FW = c W A A 2 Stirnfläche des Gegenstandes ρ ×ν 2 cW ρν 2 2 dynamischer Druck Widerstandsbeiwert Will man den Strömungswiderstand berechnen, so muss man beachten, dass reale Flüssigkeiten beim Umströmen von Gegenständen Wirbel ausbilden, wenn eine bestimmte Geschwindigkeit erreicht wird. Abb. 197: Laminare Strömung um einen Ball. Ideale Flüssigkeit, keine Wirbel. 264 BIOPHYSIK DER ZELLE Abb. 198: Turbulente Strömung mit Wirbelschleppe. Reale Flüssigkeit, mit Wirbeln. Ob nun eine laminare Strömung oder eine Strömung mit Wirbeln auftritt, wird durch die Reynoldszahl festgelegt. Bei einer laminaren Strömung verlaufen die Molekülschichten weitgehend parallel. Bei einer turbulenten Strömung beobachtet man Verwirbelungen in den Molekülschichten, sie laufen nicht mehr parallel. Erreicht die Reynoldszahl einen kritischen Wert, so geht die ideale laminare Strömung in eine turbulente über. Re = ην ρν l ν l = η ην = kinematische Viskosität = Länge der Strömung Die Strömungsform hängt also von der Viskosität der Flüssigkeit und von der Strömungsgeschwindigkeit ab. Literatur 1. Physikalische Chemie und Biophysik G. Adam, P. Läuger, G. Stark Springer-Verlag, Berlin - Heidelberg - New York, 1995 (3. Auflage) 265