folien8
Werbung

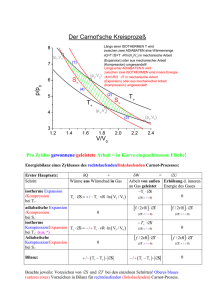
2.4. Reale Gase 2.5. Erster Hauptsatz der Thermodynamik innere Energie, Arbeit, Wärme Vorzeichenkonvention Arbeit in der Thermodynamik - Adiabatische Expansion Wärme, Wärmekapazität, Enthalpie Berechnung von U,H,Cp,CV für ein Ideales Gas - kinetische Gastheorie Berechnung von U,H, Cp,CV für reale Gase (reale Stoffe) aus molekularen Eigenschaften Messung von U,H für reale Stoffe -Verknüpfung von U, H mit leicht messbaren Größen 2.6. Thermochemie Reaktionslaufzahl χ Reaktionsenergien und –enthalpien: rU ,rH Hess'scher Satz Phasenumwandlungen: mH Schmelz- vH Verdampfungs- .sH Sublimationsenthalpie Standardzustand (1bar, 25°C) Symbol: o Standardbildungsenthalpie H o f Standardbildungsenthalpie der Elemente und von H+(aq) := 0 Kirchhoffscher Satz (Temperaturabhängigkeit von Reaktionsenthalpien) Born-Haber-Kreisprozess Kirchhoff‘scher Satz (Temperaturabhängigkeit von H) ? Temperatur T Edukte gesucht: ΔrH(T) Produkte Δ f H(T) Edukte Produkte T T Edukte Edukte Cp (T)dT 298K Pr odukte ΔrH(298 K) Δf H o Cp (T)dT 298K Edukte 298 K Δ f H(T) Produkte Produkte o Δf H Na (g) e (g) Cl(g) -351 kJ/mol Elektronenanlagerung an Cl = -Elektronenaffinität Dissoziation von Cl2 +122 kJ/mol Na (g) e (g) 1 Cl2 (g) 2 Na (g) Cl (g) Na+ und Cl- Ionen in der Gasphase +498 kJ/mol Ionisierung von Na Na(g) 1 Cl2 (g) gesucht: 2 Gitterenthalpie +107 kJ/mol von NaCl Sublimation von Na Na(s) 1 Cl2 (g) 2 +411 kJ/mol NaCl (s) festes Kochsalz NaCl (s) Spaltung von NaCl (s) in die Elemente = -Bildungsenthalpie von NaCl(s) 2.4. Reale Gase 2.5. Erster Hauptsatz der Thermodynamik 2.6. Thermochemie Reaktionslaufzahl χ Reaktionsenergien und –enthalpien: rU ,rH Hess'scher Satz Phasenumwandlungen: mH Schmelz- vH Verdampfungs- .sH Sublimationsenthalpie Standardzustand (1bar, 25°C) Symbol: Standardbildungsenthalpie f H o o Standardbildungsenthalpie der Elemente und von H+(aq) := 0 Kirchhoffscher Satz (Temperaturabhängigkeit von Reaktionsenthalpien) Born-Haber-Kreisprozess 2.7 Zweiter Hauptsatz der Thermodynamik Quelle: Atkins „Es gibt keinen periodischen Kreisprozess, der nichts anderes tut als Wärme von einem kälteren in einen wärmeren Körper zu pumpen ohne dabei einen bestimmten Betrag von Arbeit in Wärme umzutauschen“ 2. Hauptsatz Clausius: TA TA qA qA Maschine Maschine qB qB TB TB TB < TA TB < TA |qA| = |qB| wg. 1. HS w |qB| + |w| = |qA| wg. 1. HS 2. Hauptsatz „Es gibt keine zyklisch arbeitende Maschine (Kreisprozess), die Wärme aus einem Reservoir nimmt und vollständig in mechanische Arbeit umwandelt ohne einen Teil der Wärme in ein kälteres Reservoir zu überführen.“ Kelvin: TA TA qA Maschine qA w Maschine w qB TB TB < TA |qA| = |w| wg. 1. HS |qB| + |w| = |qA| wg. 1. HS Reversible Carnot-Maschine (mit idealem Gas als Arbeitsmedium) TA p qA Maschine w qB TTBB TTBB<< TTAA |qB| + |w| = |qA| wg. 1. HS Isothermen Isothermen V Reversible Carnot-Maschine (mit idealem Gas als Arbeitsmedium) p 1 TA T1,p1,V1 qA Adiabaten Maschine w T1 = T2 = TA qA Reservoir A bei TA qB Adiabaten TTBB TTBB<< TTAA 2 T4,p4,V4 |qB| + |w| = |qA| wg. 1. HS T2,p2,V2 T3,p3,V3 4 3 T3 = T4 = TB Reservoir B bei TB qB Isothermen Isothermen V Rückwärtslaufende CarnotMaschine p 1 TA T1,p1,V1 qA Adiabaten Maschine w T1 = T2 = TA qA Reservoir A bei TA qB Adiabaten TTBB TTBB<< TTAA 2 T4,p4,V4 |qB| + |w| = |qA| wg. 1. HS T2,p2,V2 T3,p3,V3 4 3 T3 = T4 = TB Reservoir B bei TB qB Isothermen Isothermen V Annahme ηs> ηc → |qAs| < |qAc| Widerspruch zu 2. HS !!! (Clausius) TA TA qAc qAs Carnot Maschine TA "super" w w qAc-qAs gekoppelte Maschine Maschinen qBs qBc-qBs qBc TB TB TB TB < TA TB < TA TB < TA |qAc| = |qBc| + |w| wg. 1. HS |qAs| = |qBs| + |w| wg. 1. HS