Angewandte Statistik – Bericht über den Nachdiplomkurs

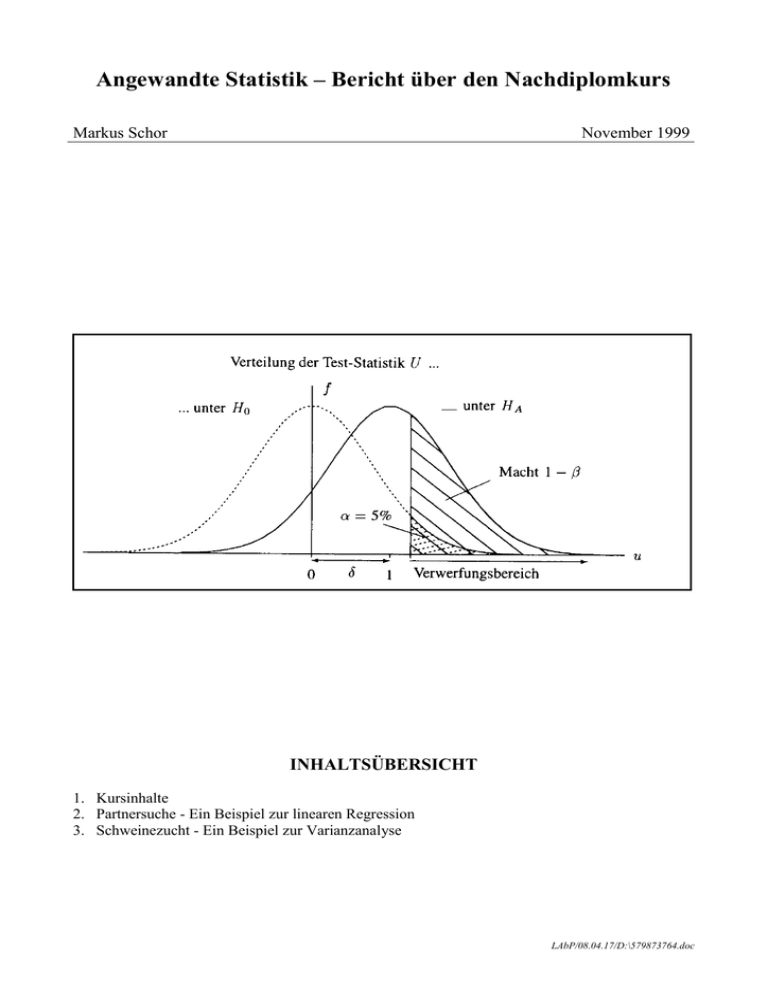
Angewandte Statistik – Bericht über den Nachdiplomkurs
Markus Schor
November 1999
INHALTSÜBERSICHT
1. Kursinhalte
2. Partnersuche - Ein Beispiel zur linearen Regression
3. Schweinezucht - Ein Beispiel zur Varianzanalyse
LAbP/08.04.17/D:\579873764.doc
Angewandte Statistik – Bericht über den Nachdiplomkurs
2. Partnersuche – Ein Beispiel zur linearen Regression
Problemstellung:
Wir betrachten eine Variable x mit festen Werten und eine Zufallsvariable Y. Es wird vermutet, dass
x eine Einfluss auf Y ausüben könnte. Es wird angenommen, dieser Zusammenhang sei ein linearer.
Unter dieser Annahme soll der Zusammenhang untersucht werden.
x heisst Einflussgrösse, Y heisst Zielgrösse.
Das Beispiel: (Nach Prof. H. Riedwyl)
In Kontaktinseraten wird häufig das Alter des Inserenten / der Inserentin angegeben, aber auch das
gewünschte Alter der Partnerin / des Partners. Uns interessiert der Zusammenhang zwischen dem
Alter der Person, von der ein Inserat stammt und dem gewünschten Alter des Partners. Das
Wunschverhalten von Männern und Frauen ist vermutlich verschieden. Darum wurden nur Inserate
von Frauen berücksichtigt, die einen Partner suchen.
In der folgenden Tabelle gibt x das Alter der Inserentin wieder, y das Wunschalter des gesuchten
Partners. Der Scatter – Plot zeigt, dass die Annahme eines linearen Zusammenhangs keineswegs
abwegig ist.
Das Modell:
Zu einem gegebenen Wert x der Einflussgrösse
ist die Zielgrösse Y normalverteilt mit einem
Mittelwert Y  x      x und einer von x
unabhängigen Standardabweichung .
Also:
Yi     xi  Ei i  1, , n 
n = Umfang der Stichprobe (im Bsp.: n = 94)
Ei = Residuen = Abweichung der Yi von ihrem
Mittelwert. Die Residuen sind normalverteilt,
Ei N  0; 
Dadurch ist die Regressionsgerade y =  + x
definiert. Allerdings sind die Parameter , 
und  unbekannt.
 = Intercept (Abschnitt auf der y – Achse)
 = Steigung
 = Standardabweichung ; misst die Streuung
der Punkte (xi;yi) um die Regressionsgerade.
1. Problem: Schätzung der Parameter
Schätzmethode: Methode der kleinsten
Quadrate
Die Summe
n
S  ,      yi     xi 
2
i 1
ist möglichst klein zu machen.
Herleitung: Siehe Anhang 1
Ergebnis:
S xy
SMin
 0.9636
=2.7769 ˆ 
ˆ 
S xx
n2
ˆ  y  ˆ x  5.4749
Gleichung der Regressionsgeraden:
y = 5.4749 + 0.9636x
Seite 3
Angewandte Statistik – Bericht über den Nachdiplomkurs
Dabei wurden folgende Abkürzungen verwendet:
x
1 n
 xi
n i 1
y
n
1 n
 yi
n i 1
n
S yy    yi  y    yi2  ny 2
i 1
S Min  S yy 
i 1
n
n
i 1
i 1
S xy    xi  x  yi  y    xi yi  nx y
i 1
S 
2
i 1
n
2
n
S xx    xi  x    xi2  nx 2
2
xy
S xx
Wunschalter des Partners
Scatter - Plot
66
64
62
60
58
56
54
52
50
48
46
44
42
40
38
36
34
32
30
28
26
24
22
20
20
22
24
26
28
30
32
34
36
38
40
42
44
46
48
50
52
54
56
58
60
62
64
66
Alter der Inserentin
ˆ , ˆ sind Zufallsvariablen.
Aus den Einflussgrössen lassen sich nun die geschätzten Werte der Zielgrössen berechnen:
yˆi  ˆ  ˆ xi
z.B.
yˆ1  5.4749  0.9636  20.5  25.2289
und daraus die beobachteten Werte der Residuen:
eˆi  yi  yˆi
z.B.
eˆ1  26  25.2289  0.7711
Im Hinblick auf die Beurteilung der gemachten Voraussetzungen ist zu überprüfen, ob die Residuen
annähernd als Stichprobe einer Normalverteilung gelten können. Ein Punktediagramm der
Wertepaare  yˆi ; eˆi  kann Aufschluss darüber bringen, ob das zugrundeliegende Modell korrekt ist.
Bei erfüllten Voraussetzungen sollten sich die Residuen im ganzen Bereich von ŷ ohne erkennbare
Struktur um 0 scharen.
Seite 4
Angewandte Statistik – Bericht über den Nachdiplomkurs
Scatter - Plot: Geschätzte y gegen Residuen
9
8
7
6
5
4
Residuen
3
2
1
0
-1
20
24
28
32
36
40
44
48
52
56
60
64
68
-2
-3
-4
-5
-6
-7
geschätzte y
2. Problem: Testen von Hypothesen
Kann man das obige Modell zur Beschreibung der Daten vereinfachen? Unter Einhaltung des
Signifikanzgrenze von 5% testen wir folgende Hypothesen:
1. Nullhypothese H0:  = 0
2. Nullhypothese H0:  = 1
gegen H1:   0
gegen H1:   1
Verwendet wird ein F – Test, basierend auf der F – Verteilung.
0
S Min
 S Min
Testgrösse:
F  H1  
S Min
n2
Freiheitsgrade:
im Zähler:
1
im Nenner: n-2 = 92
0
S Min = Minimale Fehlerquadratsumme unter der Nullhypothese
Signifikanzniveau: 5%
H0 wird verworfen, wenn gilt:
F  H1  > F0.95(1;92) (= 95% - Quantil der F – Verteilung)
Aus der Tabelle gewinnt man den Wert: F0.95(1;92) = 3.9445
1. Test:
Nullhypothese H0:  = 0
Unter H0 reduziert sich unser Modell zu:
Alternativhypothese H1:   0
Y  x    x
2
0
S Min


i xi yi  i xi yi 


= 912.0383
 xi 2
 xi 2
i

(Herleitung Anhang 2)
i
F  H1  =26.2715 > F0.95(1;92) = 3.9445

Seite 5
H0:  = 0 wird verworfen
Angewandte Statistik – Bericht über den Nachdiplomkurs
Eine Modellvereinfachung dieser Art ist nicht geeignet. Wir gehen also davon aus, dass die Gerade,
die das Wunschalter in Abhängigkeit vom Alter der Inserentinnen darstellt, nicht durch den
Ursprung des Koordinatensystems geht. Das Wunschalter des Partners ist also nicht proportional
zum Alter der Inserentin.
2. Test:
Nullhypothese H0:  = 1
Unter H0 reduziert sich unser Modell zu:
Alternativhypothese H1:   1
Y  x     x
Jetzt muss  neu geschätzt und die Testgrösse berechnet werden.
ˆ0  y  x =4.25
0
SMin
 S yy  Sxx  2Sxy = 720.375

F  H1  =1.4169 < F0.95(1;92) = 3.9445

Die Nullhypothese H0:  = 1 kann nicht verworfen werden.
Das Modell
Y  x   4.25  x
Wunschalter des Partners = 4.25 + Alter der Inserentin
beschreibt also die Situation innerhalb der gesetzten Signifikanzgrenze von 5%.
Scatterplot der Residuen vom obigen Modell:
Scatterplot der Residuen im definitiven Modell
8
6
4
Residuen
2
0
0
5
10
15
20
25
30
35
40
-2
-4
-6
-8
y = 4.25 +x
Seite 6
45
50
55
60
65
70
75
Angewandte Statistik – Bericht über den Nachdiplomkurs
Regressionsgerade im Scatterplot:
Seite 7
Angewandte Statistik – Bericht über den Nachdiplomkurs
3. Schweinezucht – Ein Beispiel zur Varianzanalyse
Problemstellung:
Die Grundlagen der Varianzanalyse (ANOVA = ANALYSIS OF VARIANCE) stammen von Sir
Ronald Fisher (F - Verteilung, F - Test). Ihn interessierte die Frage: Unterscheiden sich die
Eigenschaften verschiedener Pflanzensorten in systematischer Weise oder nur zufällig?
Die ANOVA untersucht also, ob sich verschiedene Gruppen grundsätzlich in einer bestimmten
Grösse (= Faktoren) unterscheiden, oder ob der beobachtete Unterschied nur zufällig ist.
Methode dazu ist ein Vergleich von Mittelwerten.
Das Beispiel:
(aus Gilbert, N. (1989) Biometrical Interpretation – Making Sense of Statistics in Biology, Oxford,
dargestellt von Dr. H.R. Roth in seinem Script zur Vorlesung „Varianzanalyse 1“)
Vier Würfe von je zwei reinrassigen Schweinegruppen und sechs Würfe aus einer Kreuzung der
beiden Rassen wurden auf das Längenwachstum pro Tag untersucht. Die Aufzucht aller Würfe
erfolgte unter gleichen Bedingungen. Die folgende Tabelle zeigt das durchschnittliche
Längenwachstum pro Tag und Wurf, sowie die Mittelwerte und Varianzen.
i=
j

reine Elternrassen
Large White
Landrace
1
2
Gruppe 1
Gruppe 2
Kreuzung
LW  Landrace
3
Gruppe 3
1
y11 = 1.07
y21 = 1.20
y31 = 1.35
2
y12 = 1.20
y22 = 1.31
y32 = 1.41
3
y13 = 0.98
y23 = 1.36
y33 = 1.40
4
y14 = 1.07
y24 = 1.27
y34 = 1.37
5
y35 = 1.36
6
y36 = 1.39
n1 = 4
y1  1.080
s12  0.0082
n2 = 4
n3 = 6
y2  1.285
y3  1.380
s32  0.0006
s22  0.0046
yi   Mittelwert der Gruppe i.
y  Mittelwert aller Beobachtungen
Total
n = 14
y  1.267
̂2e  0.0037
si2  Varianz der Gruppe i.
Frage: Sind die beobachteten Unterschiede im Längenwachstum zufällig, oder unterscheiden sich
die Rassen darin grundsätzlich.
Einen ersten Vergleich der Gruppen bietet das folgende Streudiagramm.
Seite 8
Angewandte Statistik – Bericht über den Nachdiplomkurs
Streudiagramm
1.4
Zuwachs pro Tag
1.3
1.2
1.1
1
0.9
0
1
2
3
4
Rasse
Das Modell:
An n Objekte in g verschiedenen Gruppen wird eine stetige Zufallsvariable Y beobachtet. Die i-te
g
Gruppe umfasst ni Beobachtungen.
n
i
n
i 1
i  1,
yij    i  eij

i    i
i
eij
,g;
j  1, ,ni 
allgemeines Niveau; feste, unbekannte Grösse
mittleres Niveau der Gruppe i
Haupteffekt / Gruppierungsfaktor; feste, unbekannte Grösse
zufälliger Fehler
Das Modell hat g + 1 Parameter bei g Gruppen. Es ist überparametrisiert. Folgende
Nebenbedingung ist nötig:
g
n 
i
i
0
i 1
Zum Modell gehören folgende Voraussetzungen:
–
Die eij setzen sich aus vielen Effekten von unbekannten oder nicht erfassbaren Faktoren
zusammen.
–
Die eij sind in allen Gruppen normalverteilt. Ihr Erwartungswert ist 0 und sie weisen alle die
gleiche Varianz  2e auf., also:
–
eij
i.i.d. N  0; e2 
 i  1,
,g;
j  1,
,ni 
(i.i.d. heisst: independent and identically distributed)
Untereinander sollen die Fehler unabhängig sein, innerhalb und zwischen den Gruppen.
Aus diesen Voraussetzungen und dem Modell folgt sofort:
E  yij   i
Var( Y )  e2
Schätzprobleme:
E  yij   i  ?
Var( Y )  e2  ?
Die i sind schätzbar. Gute Schätzer sind die Mittelwerte der Gruppen. Also:
ˆ i  yi 
ˆ  y


Seite 9
i  ?
Angewandte Statistik – Bericht über den Nachdiplomkurs
Im Beispiel:
ˆ 1  y1  1.080 ;

ˆ 2  y2  1.285 ;

ˆ 3  y3  1.380 ;

ˆ  y  1.267

2
1 ni
yij  yi  


ni  1 j 1
Die resultierenden Werte sind in obiger Tabelle ersichtlich.
Die Varianz aller Beobachtungen gemeinsam wird mit dem gewogenen Mittel geschätzt:
si2 
Die Varianzen der Gruppen:
g
g
ˆ 

2
e
  ni  1 si2
i 1
g
  n  1
ˆ 2e 

  y
ij

i 1 j 1
 yi  
ng
i
i 1
im Beispiel:
ni
3s  3s  5s
 0.0037
3 3 5
2
1
2
2
2
3
Schätzung der Haupteffekte i:
Modell:
yij    i  eij
Voraussetzung:
i  1, ,g;
i.i.d. N  0; e2   i  1, ,g;
eij
g
n 
Nebenbedingung:
i
i
j  1, ,ni 
,ni 
j  1,
0
i 1
yij    i  eij

ni
ni
j 1
j 1
 ni

  eij  0, gemäss Voraussetzung 
 j 1

 yij  ni y  nii   eij
ˆ i  yi   y

ˆ 2  0.018
ˆ 3  0.113


 ni yi   ni y  ni i 
ˆ 1  0.187
im Beispiel: 
Testprobleme:
Mit der einfachen Varianzanalyse wird ein Globaltest durchgeführt.
Nullhypothese:
Zwischen den Gruppen gibt es keine Unterschiede
Alternativhypothese: Mindestens eine Gruppe unterscheidet sich von den andern.
Im Beispiel:
H0:
1 = 2 = 3
oder:
H1:
für mindestens ein i gilt: i  0
Es gilt:
(Herleitung siehe Anhang 4)
g
ni
  y
i 1 j 1
SQ(total)
SQ(zwischen)
g
g
ni
ij  y     ni  yi   y      yij  yi  
2
2
i 1
2
i 1 j 1
SQ  total 
= SQ  zwischen  + SQ  innerhalb 
FG  total 
= FG  zwischen  + FG  innerhalb 
n 1
FG
SQ
1 = 2 = 3 = 0

 g  1

n  g 
= Freiheitsgrade
= Summe der quadrierten Abweichungen
(kurz: Summe der Quadrate / engl: sum of squares, SS)
= SQ der beobachteten Werte vom totalen Mittelwert.
= SQ der Gruppenmittel vom totalen Mittel
Seite 10
Angewandte Statistik – Bericht über den Nachdiplomkurs
SQ(innerhalb)
= SQ der beobachteten Werte vom zugehörigen Gruppenmittel
Mit der Schätzung der Haupteffekte ergibt sich noch die Beziehung:
g
g
ˆ i
SQ  zwischen    ni  yi   y    ni  
2
i 1
2
i 1
Dividiert man die SQ – Werte durch die entsprechenden Freiheitsgrade, erhält man die
„durchschnittliche quadratische Abweichung“ DQ (kurz: Durchschnittsquadrate / engl: mean squares, MS)
Die Testgrösse:
F=
DQ  zwischen 
DQ  innerhalb 
folgt unter H0 einer F – Verteilung
mit g – 1 Freiheitsgraden im Zähler und
mit n – g Freiheitsgraden im Nenner.
H0 wird verworfen, wenn F > Tabellenwert der entspr. F – Verteilung.
Daraus ergibt sich die typische Tabelle für eine Einweg – Varianzanalyse:
ANOVA
FG
SQ
Zwischen den Gruppen
g–1
SQ(zwischen)
DQ(zwischen)
Innerhalb der Gruppen
n–g
SQ(innerhalb)
DQ(innerhalb)
Total
n–1
SQ(total)
DQ =
SQ
FG
F=
DQ  zwischen 
DQ  innerhalb 
Im Beispiel ergeben sich folgende Werte:
ANOVA
FG
SQ
Zwischen den Rassen
3 – 1 =2
0.2178
0.1089
Innerhalb der Rassen
14 – 3 = 11
0.0411
0.0037
Total
14 – 1=13
0.2589
DQ =
SQ
FG
F=
DQ  zwischen 
DQ  innerhalb 
29.144
Der Wert aus der F – Verteilung mit 2 und 11 Freiheitsgraden beträgt 3.9823 (Tabelle).
 F = 29.144 > 3.9823  H0 muss verworfen werden.
Antwort:
Die drei Gruppen haben kein einheitliches Niveau. Die beobachteten Unterschiede im
Längenwachstum sind nicht zufällig.
Seite 11