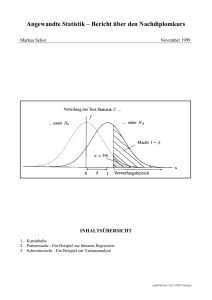
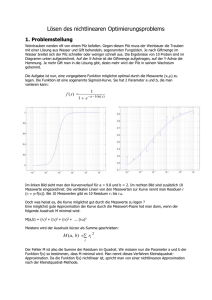
strategie

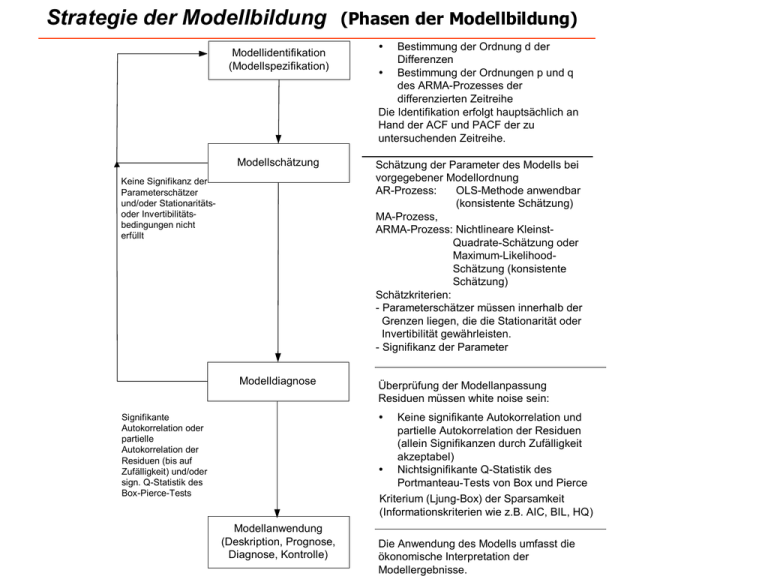
Strategie der Modellbildung
Modellidentifikation
(Modellspezifikation)
(Phasen der Modellbildung)
Ÿ
Bestimmung der Ordnung d der
Differenzen
Ÿ Bestimmung der Ordnungen p und q
des ARMA-Prozesses der
differenzierten Zeitreihe
Die Identifikation erfolgt hauptsächlich an
Hand der ACF und PACF der zu
untersuchenden Zeitreihe.
Modellschätzung
Schätzung der Parameter des Modells bei
vorgegebener Modellordnung
AR-Prozess:
OLS-Methode anwendbar
(konsistente Schätzung)
MA-Prozess,
ARMA-Prozess: Nichtlineare KleinstQuadrate-Schätzung oder
Maximum-LikelihoodSchätzung (konsistente
Schätzung)
Schätzkriterien:
- Parameterschätzer müssen innerhalb der
Grenzen liegen, die die Stationarität oder
Invertibilität gewährleisten.
- Signifikanz der Parameter
Modelldiagnose
Überprüfung der Modellanpassung
Residuen müssen white noise sein:
Keine Signifikanz der
Parameterschätzer
und/oder Stationaritätsoder Invertibilitätsbedingungen nicht
erfüllt
Ÿ
Keine signifikante Autokorrelation und
partielle Autokorrelation der Residuen
(allein Signifikanzen durch Zufälligkeit
akzeptabel)
Ÿ Nichtsignifikante Q-Statistik des
Portmanteau-Tests von Box und Pierce
Kriterium (Ljung-Box) der Sparsamkeit
(Informationskriterien wie z.B. AIC, BIL, HQ)
Signifikante
Autokorrelation oder
partielle
Autokorrelation der
Residuen (bis auf
Zufälligkeit) und/oder
sign. Q-Statistik des
Box-Pierce-Tests
Modellanwendung
(Deskription, Prognose,
Diagnose, Kontrolle)
Die Anwendung des Modells umfasst die
ökonomische Interpretation der
Modellergebnisse.
Modellschätzung
• Schätzung eines AR(p)-Modells
X t  1X t 1  2X t  2    p X t  p  Ut
Substitution der Autokorrelationen  durch die Stichprobenkorrelationen r in die YuleWalker-Gleichungen: k  1k 1  2k 2    pk p , k  1

r1  1
r  r
 2   1
  
  
rp  rp 1
kompakt:

r1
r2
1
r1


rp  2 rp 3




rp 1   1 
rp  2  2 
 

 
  
1   p 
r  R 
1
 1
Auflösen des Gleichungssystems nach dem Koeffizientenvektor  (falls Inverse von R
existiert):
ˆ
  R 1  r


ˆ1, ˆ 2 ,, ˆ p des Parametervektors   1 , 2 ,  ,  '
̂ enthält die geschätzten Parameter 
eines AR(p)-Modells.
.
Beispiel:
1  r1
AR(1)-Modell: r1  1  ˆ
r  1  2r1
AR(2)-Modell: 1
r2  1r1  2
 r1   1



| r2  r1
R 1 
 1

1  r12   r1
 r1 
1 
ˆ

 1

1  r12   r1
 r1 
1 
ˆ
1 
1
1
r1  r1  r2
1  r12
,
ˆ
2 
r1 
1 
 1 
 
 2
r1 
1 r1  r1  r2 

r 
2  r  r2 
2
1

r
 
1 
1  2
r2  r12
1  r12
• Schätzung von MA-Modellen
(nach Box und Jenkins, 1970; vgl. auch Chatfield, 1980)
 MA(1)-Modell: Xt    U t  1  Ut 1
Ein Schätzer für den Parameter 1 könnte zwar aus der Bestimmungsgleichung für den
Autokorrelationskoeffizienten 1. Ordnung
ˆ
1


ˆ
1
(1)
1  12
unter Berücksichtigung der Bedingung ˆ
1  1 ermittelt werden, doch hätte eine solche
Schätzfunktion nur eine geringe Effizienz.
Box und Jenkins schlagen daher ein Iterationsverfahren vor, in dem folgende Startwerte
ˆ (0)  x und ˆ1(0) gemäß (1) 
für  und 1 verwendet werden:
Aus (1) folgt (quadratische Gleichung in ̂1 )
ˆ1ˆ12  ˆ1  ˆ1  ˆ1ˆ12  ˆ1  ˆ1  0
1
 ˆ12  ˆ1  1  0
ˆ
b
1
Norma lg leichung 
a
Lösung der quadratischen Gleichung
2
a
a
1


1
/
2
ˆ1       b 

ˆ
2
2
2

 
1
2
 1 

  1
ˆ
2

 1
Dann werden zunächst die Residuen rekursiv berechnet. Die Rekursionsgleichungen sind
allgemein im l-ten Iterationsschritt durch
u1()  x1  ()  1()u(0) und da u(0) stets
( )
( )
.
gleich 0 gesetzt wird: u1  x1  
u(2)  x 2  ()  1()u1()
u(3)  x 3  ()  1()u(2)



un()  xn  ()  1()un()1
Es kann dann die Summe der quadrierten Residuen bestimmt werden:


n
Q  , 1    u2t()
.
t 1
Die Iteration wird für alternative Werte für  und 1 durchgeführt, die mittels eines
    -Ebene festgelegt werden. Als Kleinst-Quadrate-Schätzer
Gitternetzes in der   , 1

1 werden diejenigen Werte für  und 1 gewählt, für die die Kriteriumsfunktion Q
ˆ und ˆ
minimal wird:


 

Q
1  Q  , 1 
ˆ, ˆ

.
Sofern die Schocks Ut normalverteilt sind, sind die Kleinst-Quadrate-Schätzer

1 zugleich Maximum-Likelihood-Schätzer.
ˆ und ˆ
[Bem.:
Das Iterationsverfahren kann verfeinert werden durch ein sog. Backforecasting zur

Bestimmung von u0 . Dies ist jedoch nur erforderlich, wenn 1 nahe an 1 oder –1
herankommt.]
Für Prozesse höherer Ordnung ist das Iterationsverfahren analog einsetzbar. So sind z.B. bei
einem MA(2)-Prozess
Xt    Ut  1Ut 1  2Ut 2
Anfangswerte 0, 10 und 20zu ermitteln, aus denen die Residuen
u(t)  x t  ()  1()u(t)1  (2)u(t)2
rekursiv ermittelt werden und die dann zur Berechnung der Residualquadratsumme Q verwendet werden. Allerdings bietet es sich bei MA-Prozessen höherer als 2. Ordnung an, auf
nichtlineare Optimierungsverfahren wie z.B. das Gradiantenverfahren zurückzugreifen, womit
eine effizientere Bestimmung der Kleinst-Quadrate-Schätzer erzielt wird.
• Schätzung eines ARMA(p,q)-Modells
X t  1X t 1  2X t  2    p X t  p  Ut  1Ut 1  2Ut  2    qUt  q
X t  1X t 1  2X t  2    p X t  p  Ut  1Ut 1  2Ut  2    qUt  q
B   X t  B   Ut
mit
B   1  1B  2B2    Bp
und
B   1  1B  2B2    qB q
Kleinst-Quadrate-Kriterium:
Q1 ,  , 2 , 1 ,  , q  
mit
n
 u2t
t  
Dahinter steht die Tatsache, dass sich ein
ARMA(p,q)-Prozess durch einen
unendlichen MA-Prozess darstellen lässt.
Dieser kann mit hinreichend großem r
durch ein MA(r)-Prozess approximiert
werden.
Min.
  u2t 
1 ,  , p , 1 ,  , q
t 1  r
n
ut  x t  1x t 1    p x t  p  1ut 1    qut  q
.
Für tmax {p,q} sind die Residuen ut jedoch nicht bestimmbar, da die ut für t0 unbekannt
sind und Startwerte für xt für t0 benötigt werden.
CLS-Schätzung (conditional least-squares)
[bedingte Kleinst-Quadrate-Schätzung]
Startwerte werden Null gesetzt: t=0 für t0
xt=0 für t0
Q ist keine quadratische Funktion der Parameter 1,...,p, 1,...,q, so dass die CLS-Schätzer
ˆ
1 ,  , ˆ
p , ˆ
1 ,  , ˆ
q mittels numerischer Optimierungsmethoden ausgehend von
bestimmten Anfangswerten iterativ bestimmt werden müssen. Als numerische
Optimierungsmethoden kommen z.B. das Newton-Raphson-Verfahren oder der MarquardtAlgorithmus in Betracht.
 
   
 
Mit den Schätzern 1 ,  , p , 1 ,  , q im  -ten Schritt erhält man die Residuen für t1
aus den Rekursionsgleichungen
u1 
u2 
u3 

un 





x1
x 2  1 x1  1 u1
x 3  1 x 2  2 x1  1 u2  2 u1
x n  1 x n 1    p x n  p  1 un 1    q un  q
Daraus lässt sich die Residuen-Quadratsumme


n




   

Q 1 ,  , p , 1 ,  , q   ut 
t 1  r
n
 
 ut  0


t 1






wegen u0  u1    u1  r  0
bestimmen. Mittels eines numerischen Optimierungsverfahrens werden neue Schätzer
1 1,  , p 1, 1 1,  , q 1 bestimmt, die die Bedingung

 
Q 1 1,  , p 1, 1 1,  , q 1  Q 1 ,  , p , 1 ,  , q 

erfüllen. Die Iteration wird so lange durchgeführt, bis das Verfahren konvergiert. Als
Konvergenzkriterium kann z.B. die maximale Differenz der Schätzwerte der Parameter
1,...,p,1,...,q zweier aufeinanderfolgender Schritte verwendet werden:
max{1 1  1 ,  , p 1  p , 1 1  1 ,  , q 1  q }  ,
0
Danach wird das Verfahren beendet, wenn die maximale Differenz zweier aufeinander
folgender Parameterschätzer kleiner oder gleich einem vorgegebenen Wert  ist.
1 1,  , p 1,  , 1 1,  , q 1 sind dann die CLS-Schätzer:
ˆ
1  1 1,  , ˆ
p  p 1, ˆ
1  1 1,  , ˆ
q  q 1
Die Residualvarianz ist durch
Qˆ
1 ,  , ˆ
p , ˆ
1 ,  , ˆ
q
2

ˆu 
npq
gegeben.

.

ULS-Schätzung (unconditional least-squares)
[unbedingte Kleinst-Quadrate-Schätzung]
Bei der unbedingten Kleinst-Quadrate-Schätzung werden Schätzwerte für x0,x-1,...,x1-r
mittels einer sog. Backforecasting-Technik ermittelt, womit die Residuen
ut  x t  1x t 1    t  p  1ut 1    qut  q
für t=1–r,...,n rekursiv bestimmt werden können. Bei gegebenen x0,x-1,...,x1-r braucht man
hierzu nur noch die Residuen ut für t<1–r gleich Null zu setzen. Das BackforecastingVerfahren schätzt die Anfangswerte x0,x-1,...,x1-r durch eine „Prognose“ der Zeitreihe in die
Vergangenheit.
• Informationskriterien
Um die Güte der Anpassung alternativer ARIMA-Modelle in Bezug auf ihre Prognosefähigkeit
zu überprüfen, sind diverse Informationskriterien entwickelt worden. Sie basieren einerseits
auf der logarithmischen Likelihood-Funktion und andererseits auf einer Straffunktion, die
dem Prinzip der Sparsamkeit bei der Modellauswahl Rechnung tragen soll. Die Likelihood-Funktion allein als Auswahlkriterium heranzuziehen, wäre nicht adäquat. Denn sie
weist stets eine bessere Modellanpassung aus, wenn das ARIMA-Modell umfangreicher wird.
Je umfangreicher das ARIMA-Modell jedoch wird, um so größer ist die Gefahr, dass nicht
signifikante Parameterschätzungen auftreten. Es werden möglicherweise Zufallsschwankungen berücksichtigt, die für die Prognose störend sein können. Die Modellschätzung
insgesamt tendiert dahin, instabil zu werden, wenn das Modell überparametrisiert ist. Zum
Schutz gegen ein derartiges „Overfitting“ wird zusätzlich eine Straffunktion (penalty
function) eingeführt, die eine sparsame Modellbildung belohnt. Auf diese Weise trägt sie
auch zu einer Selektion stabiler ARIMA-Modelle bei, die im Hinblick auf eine Prognose umfangreicheren Modellen vorzuziehen sind.
Die logarithmierte Likelihood-Funktion eines ARMA(p,q)-Modells wird aus der gemeinsamen Dichtefunktion der multivariat verteilten Zufallsvariablen X1,X2,...,Xn bestimmt:
(6)
 p, q , θ | x   ln f x | , θ
.
Die Vektoren  und θ enthalten darin die Koeffizienten der MA- bzw. AR-Terme des ARMAModells. Für die Maximum-Likelihood-Schätzer ̂ und θ̂ der Parameter des ARMA-Modells
wird die logarithmierte Likelihood-Funktion maximal:
( 7)


 p,q ˆ , θˆ | x  max , θ | x  .
,θ
Das bedeutet, dass ein ARMA-Modell bei gegebenen p und q größte „likelihood“ besitzt und
damit die beste Anpassung aufweist, wenn seine Parameter durch ̂ und θ̂ geschätzt
werden. Man kann nun zeigen, dass der maximale Wert der logarithmierten Likelihood2 des ARMA (p,q)-Modells abhängig ist:
Funktion entscheidend von der Residualvarianz σ̂p,q
n
2
( 8)
 p, q ˆ
, θ̂ | x  C  ln 
ˆp, q .
2
C ist darin eine Konstante, die für die Modellselektion nicht von Bedeutung ist. Je mehr
Parameter das ARMA-Modell umfasst, um so kleiner wird die Residualvarianz und um so
größer wird damit der maximale Wert der Likelihood-Funktion. Somit gilt für p’p und q’q
stets





 p',q' ˆ , θˆ | x   p,q ˆ , θˆ | x

.
Eine Erweiterung des ARMA-Modells kann folglich unter keinen Umständen zu einer
Verschlechterung der Modellanpassung führen.
In den Informationskriterien geht die logarithmierte Likelihood-Funktion in der
Modifikation
2
2
( 9)
ln 
, θ̂ | x
ˆp, q    p, q ˆ
n
ein.


Akaikes Informationskriterium AIC kann in der Hinsicht interpretiert werden, dass ein
umfangreiches ARMA-Modell dadurch „bestraft“ wird, dass die p+q Parameter von der
maximierten Loglikelihood subtrahiert werden. Die Straffunktion ist dann einfach durch die
Anzahl der Parameter eines ARMA-Modells gegeben. Unter Berücksichtigung der Modifikation
(9) ist das AIC-Kriterium durch
(10)
2
AICp, q  ln 
ˆp, q 
2
p  q
n
gegeben. Auf der Grundlage dieses Kriteriums ist dasjenige ARMA-Modell vorzuziehen, das
zu einem minimalen AIC-Wert führt. Die Erweiterung eines ARMA-Modells mit gegebenem p
und q kann sowohl zu einem größeren als auch zu einem kleineren AIC-Wert führen. Denn
bei einer Erhöhung der Parameterzahl sinkt zwar die Residualvarianz, aber es steigt der Wert
der Straffunktion. Welcher der beiden Effekte letztlich dominiert, lässt sich a priori nicht
voraussagen.
Wie gut arbeitet nun das AIC-Kriterium? Eine wünschenswerte Eigenschaft wäre es,
wenn das korrekte ARMA-Modell auf der Grundlage des AIC-Kriteriums fast sicher selektiert
werden könnte, wenn der Stichprobenumfang, d.h. die Länge der Zeitreihe, immer größer
wird. Diese Eigenschaft der Konsistenz erfüllt das AIC-Kriterium jedoch nicht. Es hat sich
gezeigt, dass das AIC-Kriterium dazu tendiert, die Modellordnung zu überschätzen. Die
verwendete Straffunktion ist nicht ausreichend. In der Zeitreihenanalyse kann das AICKriterium unter diesem Aspekt verwendet werden, um eine obere Grenze der Modellordnung
festzulegen.
Ein konsistentes Informationskriterium ist dagegen das Bayessche Informationskriterium BIC:
(11)
2
BICp, q  ln 
ˆp, q 
ln n
p  q
n
.
Es ist ähnlich zu interpretieren wie das AIC-Kriterium, jedoch wird eine höhere
Modellordnung beim BIC-Kriterium stärker bestraft.
Ebenfalls konsistent ist das Hannan-Quinn-Kriterium HQ,
(12)
2
HQ p, q  ln 
ˆp, q 
c  lnln n
p  q , c  1
n
,
das sich von den Informationskriterien AIC und BIC durch die Straffunktion unterscheidet. c
ist hierin eine wählbare Konstante, über die keine konkreten Aussagen gemacht werden. Die
Restriktion c>1 sichert die Konsistenz dieses Kriteriums.
In der Praxis der Zeitreihenanalyse empfiehlt sich eine vorsichtige Anwendung der Informationskriterien AIC und BIC bei der Modellauswahl. Beide Kriterien können eine Residuenanalyse zur Aufdeckung von Ausreißern und Verteilungsanomalitäten nicht ersetzen. Sie
sollten erst dann angewendet werden, wenn diese Probleme hinreichend gelöst sind.