Primzahlen
Werbung
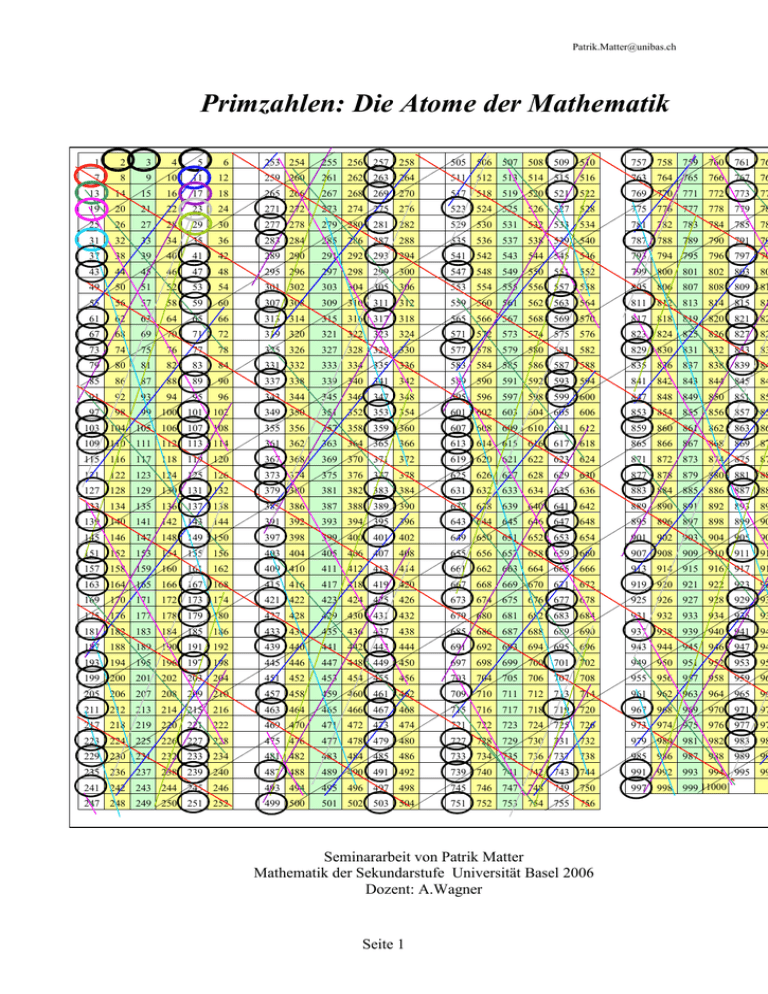
[email protected] Primzahlen: Die Atome der Mathematik 1 2 3 4 5 6 253 254 255 256 257 258 505 506 507 508 509 510 757 758 759 760 761 76 7 8 9 10 11 12 259 260 261 262 263 264 511 512 513 514 515 516 763 764 765 766 767 76 13 14 15 16 17 18 265 266 267 268 269 270 517 518 519 520 521 522 769 770 771 772 773 77 19 20 21 22 23 24 271 272 273 274 275 276 523 524 525 526 527 528 775 776 777 778 779 78 25 26 27 28 29 30 277 278 279 280 281 282 529 530 531 532 533 534 781 782 783 784 785 78 31 32 33 34 35 36 283 284 285 286 287 288 535 536 537 538 539 540 787 788 789 790 791 79 37 38 39 40 41 42 289 290 291 292 293 294 541 542 543 544 545 546 793 794 795 796 797 79 43 44 45 46 47 48 295 296 297 298 299 300 547 548 549 550 551 552 799 800 801 802 803 80 49 50 51 52 53 54 301 302 303 304 305 306 553 554 555 556 557 558 805 806 807 808 809 81 55 56 57 58 59 60 307 308 309 310 311 312 559 560 561 562 563 564 811 812 813 814 815 81 61 62 63 64 65 66 313 314 315 316 317 318 565 566 567 568 569 570 817 818 819 820 821 82 67 68 69 70 71 72 319 320 321 322 323 324 571 572 573 574 575 576 823 824 825 826 827 82 73 74 75 76 77 78 325 326 327 328 329 330 577 578 579 580 581 582 829 830 831 832 833 83 79 80 81 82 83 84 331 332 333 334 335 336 583 584 585 586 587 588 835 836 837 838 839 84 85 86 87 88 89 90 337 338 339 340 341 342 589 590 591 592 593 594 841 842 843 844 845 84 91 92 93 94 95 96 343 344 345 346 347 348 595 596 597 598 599 600 847 848 849 850 851 85 97 98 99 100 101 102 349 350 351 352 353 354 601 602 603 604 605 606 853 854 855 856 857 85 103 104 105 106 107 108 355 356 357 358 359 360 607 608 609 610 611 612 859 860 861 862 863 86 109 110 111 112 113 114 361 362 363 364 365 366 613 614 615 616 617 618 865 866 867 868 869 87 115 116 117 118 119 120 367 368 369 370 371 372 619 620 621 622 623 624 871 872 873 874 875 87 121 122 123 124 125 126 373 374 375 376 377 378 625 626 627 628 629 630 877 878 879 880 881 88 127 128 129 130 131 132 379 380 381 382 383 384 631 632 633 634 635 636 883 884 885 886 887 88 133 134 135 136 137 138 385 386 387 388 389 390 637 638 639 640 641 642 889 890 891 892 893 89 139 140 141 142 143 144 391 392 393 394 395 396 643 644 645 646 647 648 895 896 897 898 899 90 145 146 147 148 149 150 397 398 399 400 401 402 649 650 651 652 653 654 901 902 903 904 905 90 151 152 153 154 155 156 403 404 405 406 407 408 655 656 657 658 659 660 907 908 909 910 911 91 157 158 159 160 161 162 409 410 411 412 413 414 661 662 663 664 665 666 913 914 915 916 917 91 163 164 165 166 167 168 415 416 417 418 419 420 667 668 669 670 671 672 919 920 921 922 923 92 169 170 171 172 173 174 421 422 423 424 425 426 673 674 675 676 677 678 925 926 927 928 929 93 175 176 177 178 179 180 427 428 429 430 431 432 679 680 681 682 683 684 931 932 933 934 935 93 181 182 183 184 185 186 433 434 435 436 437 438 685 686 687 688 689 690 937 938 939 940 941 94 187 188 189 190 191 192 439 440 441 442 443 444 691 692 693 694 695 696 943 944 945 946 947 94 193 194 195 196 197 198 445 446 447 448 449 450 697 698 699 700 701 702 949 950 951 952 953 95 199 200 201 202 203 204 451 452 453 454 455 456 703 704 705 706 707 708 955 956 957 958 959 96 205 206 207 208 209 210 457 458 459 460 461 462 709 710 711 712 713 714 961 962 963 964 965 96 211 212 213 214 215 216 463 464 465 466 467 468 715 716 717 718 719 720 967 968 969 970 971 97 217 218 219 220 221 222 469 470 471 472 473 474 721 722 723 724 725 726 973 974 975 976 977 97 223 224 225 226 227 228 475 476 477 478 479 480 727 728 729 730 731 732 979 980 981 982 983 98 229 230 231 232 233 234 481 482 483 484 485 486 733 734 735 736 737 738 985 986 987 988 989 99 235 236 237 238 239 240 487 488 489 490 491 492 739 740 741 742 743 744 991 992 993 994 995 99 241 242 243 244 245 246 493 494 495 496 497 498 745 746 747 748 749 750 997 998 999 11000 247 248 249 250 251 252 499 500 501 502 503 504 751 752 753 754 755 756 Seminararbeit von Patrik Matter Mathematik der Sekundarstufe Universität Basel 2006 Dozent: A.Wagner Seite 1 [email protected] 1 2 3 4 5 6 7 8 9 Einleitung ........................................................................................................................... 3 1.1 Hintergrund ................................................................................................................ 3 1.2 Grundlagen ((auch)für Laien verständlich) ................................................................ 3 Definition der Primzahlen .................................................................................................. 6 2.1 Einige Eigenschaften von Primzahlen........................................................................ 6 Unendliche Menge der Primzahlen .................................................................................... 7 3.1 Beweis von Euklid ..................................................................................................... 7 3.2 Beweis von Goldbach(1730) ...................................................................................... 8 3.3 Beweis von Euler ....................................................................................................... 8 Wie erkennt man Primzahlen ............................................................................................. 9 4.1 Einfache Zerlegung .................................................................................................... 9 4.2 Sieb des Erastothenes ............................................................................................... 11 4.3 Test mit dem kleinen Lehrsatz von Fermat .............................................................. 12 4.4 Agrawal-Kayal-Saxena-Primzahltest(2004) ............................................................ 12 Besondere Arten von „Primzahlen“ ................................................................................. 13 n 5.1 Fermatzahlen ( Fn 2 2 1 n 0 ) .......................................................................... 13 5.2 Mersenne-Primzahlen( M p 2 p 1 ) für p P ...................................................... 14 5.3 Pseudoprimzahlen .................................................................................................... 14 5.4 Primzahlzwilinge ...................................................................................................... 14 5.5 Primzahlvierlinge ..................................................................................................... 15 5.6 Primzahlsechslinge ................................................................................................... 15 Bedeutung der Primzahlen ............................................................................................... 15 6.1 Histortische Bedeutung ............................................................................................ 15 6.2 Mathematische Bedeutung: Fundamentalsatz der Arithmetik ................................. 16 6.3 Kryptografie: Praktische Anwendung der Primzahlen ............................................. 16 Primzahlen in der Schule Sek1-Inputs ............................................................................. 17 7.1 Primzahlen als Hauptthema ...................................................................................... 18 7.1.1 Aufgaben im Rekord-Stil 7.1.2 Aufgaben im Internet ....................................................................................... 18 7.1.3 Aufgaben mit Teilbarkeitsregeln ...................................................................... 18 7.1.4 Sieb von Erathosthenes .................................................................................... 18 7.1.5 Einfache Primzahlbeweise ............................................................................... 18 7.1.6 Primfaktorenzerlegung ..................................................................................... 19 7.2 Primzahlen in Neben-Themen .................................................................................. 19 7.2.1 Kürzen und Erweitern ...................................................................................... 19 7.2.2 Parallelverschiebung ........................................................................................ 19 7.2.3 Beweise ............................................................................................................ 19 7.2.4 Repetition der Reihen ....................................................................................... 19 7.3 Primzahlen in Fachübergreifenden Themen / Themen für Projektarbeiten ............. 19 7.3.1 Mathematiker und ihre Beweise(Geschichte, Mathematik) ............................. 20 7.3.2 Krypografie (Geschichte, Mathematik, Deutsch)............................................. 20 7.3.3 Krypografie (Geschichte, Mathematik, Deutsch)............................................. 20 7.3.4 Primzahlen auf dem Internet (Mathematik, Informatik) .................................. 20 Glossar .............................................................................................................................. 20 Quellen und Links ............................................................................................................ 21 Seite 2 [email protected] 1 Einleitung 1.1 Hintergrund Im Rahmen meiner Ausbildung zum Sekundarlehrer ist es vorgegeben, zwei Semesterarbeiten zu verfassen. Für die zweite dieser Arbeiten habe ich mich für das Thema „Primzahlen“ entschieden. Da ich es spannend finde mich einmal mit diesen Atomen der Mathematik bzw. der Zahlen etwas näher zu befasse. Und mir der spielerische Aspekt des Themas (Primzahlrekorde, ausgesetzte Prämien für die erste Primzahl mit mehr als 10'000'000 Stellen bezahlt werden, etc) ideal erscheint um den Schülern und Schülerinnen die Freude an der Mathematik näher zu bringen. Da es mir ein Anliegen ist, dass meine Arbeit auch von interessierten Laien gelesen und verstanden werden kann, führe ich zuerst in einem allgemeinen Theorieteil die mathematischen Grundlagen ein, die zum Verständnis meiner Arbeit benötigt werden. Anschliessend gebe ich einen Überblick über das Thema Primzahlen den Schluss meiner Arbeit bilden einige Inputs zum Thema: Primzahlen im Mathematikunterricht aus der Sekundarstufe1. 1.2 Grundlagen ((auch)für Laien verständlich) 1.2.1 Beweisverfahren 1.2.1.1 Direkter Beweis Bei einem direkten Beweis ist es möglich einen Sachverhalt durch mathematische (logische) Umformungen herzuleiten. Oft werden dazu auch andere bereits bewiesene Tatsachen verwendet. z.B: Beweis des Grenzwerts der geometrischen Reihe (1.2.5) 1.2.1.2 Indirekter Beweis oder Beweis durch Widerspruch Eine Annahme wird bewiesen, in dem bewiesen wird, dass ihre Gegenannahme zu einem Widerspruch führt. z.B Lemma von Euklid (2.1.2) 1.2.1.3 Beweis durch vollständige Induktion Bei einem Beweis mit Hilfe der vollständigen Induktion, stellt man ein Annahme: (Für jedes nte Element gilt …..) auf. 1. Zeigt man, dass diese Behauptung für das erste Element stimmt. 2. zeigt man, dass die Behauptung auch für jedes (n+1) Element stimmt. Seite 3 [email protected] z.B: Eigenschaften der Fermatzahlen (5.1.1) 1.2.2 Zahlenmengen N = {1, 2, 3, …. } ist die Menge der natürlichen Zahlen ohne 0! N0 ={0, 1, 2, 3, ….}ist die Menge der Natürlichen Zahlen mit 0! Z = {…,-1,0,1,…) ist die Menge der ganzen Zahlen! P = {p1, p2, p3,…} ist die Menge aller Primzahlen! 1.2.3 Grösster gemeinsamer Teiler(ggT) Der grösste gemeinsame Teiler ist die grösste Zahl, die zwei Zahlen ohne Rest teilen kann. Man findet ihn wenn man beide Zahlen in ihre Primfaktoren zerlegt. Der ggT ist das Produkt der gemeinsamen Glieder (Primfaktoren mit Potenz). a (( p1 ) 2 p 2 ( p3 ) 2 ....) b ( p1 ( p 2 ) 0 ( p3 ) 3 ...) ggT (a, b) ( p1 ( p 2 ) 0 ( p3 ) 2 ...) 360 (2 3 32 5) 700 (2 2 5 2 7) ggT (360,700) (2 2 5) 20 1.2.4 Polynomischer Lehrsatz p p p p k k p! a b (a b) p a p k b k k 0 k k 0 k! ( p k! ) 1.2.5 Geometrische Reihe a(1 q n1 ) s n a aq aq ... aq ) a q 1 q k 0 n 2 Beweis: n k s n a(1 q q 2 ... q n ) und s n q a(q q 2 ... q n 1 ) s n q s n s n (q 1) a[( q q 2 ... q n 1 ) (1 q q 2 ... q n )] a[q n 1 1] a[q n1 1] sn (q 1) 1.2.6 Kongruenz 1.2.6.1.1 Definition Zwei Zahlen sind kongruent eines Moduls (einer weiteren Zahl), wenn sie bei der Divison durch das Modul denselben Rest haben. oder Seite 4 [email protected] Zwei Zahlen a und b sind kongruent modulo m, wenn m die Differenz a − b teilt. oder ab n (mit n Z ) a b (mod m) m Bsp: 7/5 =1 Rest 2 7 2 (mod 5) 1.2.6.1.2 Regeln für das Rechnen mit Kongruenzen Für (a, a' , b, b' , c, x, m) Z , m 0, p P und x x' (mod m) gilt: Symmetrie: a b (mod m) b a (mod m) Transitivität: a b (mod m) und b c (mod m) a c (mod m) ca ca ' (mod m) a b a'b' (mod m) ab a'b' (mod m) „Kürzen“: ca cb (mod m) a b ( mod m ) ggT (c, m) ca cb (mod p) a b (mod p) a n (a' ) n (mod m) a ( m ) 1 (mod m) Seite 5 [email protected] 1.2.7 Die eulersche Phi-Funktion Euler fand eine Funktion die es ermöglicht herauszufinden, wie viele Zahlen a mit ggT (a, n) 1 es unterhalb einer Zahl n hat. n n i 1 i 11 (n) pi k 1 ( pi 1) n (1 1 ) pi 1 p ( p k ) p k 1 ( p 1) p k (1 ) ( p) p 1 Satz: (nm) (n) (m) für ggT (n, m) 1 s ,r Beweis: (nm) nm (1 i 1, j 1 s r 1 1 1 1 )(1 ) (n) (m) n (1 )m (1 ) pi qj p i j 11 qj i 1 2 Definition der Primzahlen Eine Primzahl ist eine natürliche Zahl mit genau zwei natürlichen Teilern, nämlich 1 und sich selbst. (Da 1 nur durch sich selbst teilbar ist, bildet das neutrale Elemente der Multiplikation und der Division auch hier eine Ausnahme!) (vgl. Wikibook: „Warum_1_keine_Primzahl_ist!“) 2.1 Einige Eigenschaften von Primzahlen 2.1.1 Eindeutigkeit der Primfaktorzerlegung: Jede natürliche Zahl lässt sich als Produkt von Primzahlen schreiben. Diese Produktdarstellung ist bis auf die Reihenfolge der Faktoren eindeutig (siehe Fundamentalsatz der Algebra 6.2) 2.1.2 Lemma von Euklid: Ist ein Produkt zweier natürlicher Zahlen durch eine Primzahl teilbar, so ist bereits einer der Faktoren durch sie teilbar. Annahme1: ab n (für n, a, b N sowie a px, b py ) p ggT ( p / a) 1 und ggT ( p / b) 1 sowie ggT ( p / ab) 1 Seite 6 ab n Widerspruch! p [email protected] 2.1.3 Goldbach-Vermutung Jede gerade Zahl grösser als vier lässt sich als Summe zweier Primzahlen schreiben. Obwohl Tomás Oliveira e Silva (2005) alle Zahlen bis 2 · 1017 als Summe zweier Primzahlen schreiben konnte und diese Wahrscheinlichkeit für grössere Zahlen immer höher wird, da mehr Primzahlen für eine Addition zur Verfügung stehen ist die Vermutung ist bis heute noch nicht bewiesen. 2.1.4 Der kleine Satz von Fermat a ( p 1) 1 (mod p) oder a p a (mod p) (für a N , ggT (a, p ) 1 und p=Primzahl ) Annahme: a p a (mod p) 1. a 1 a (mod 1) 2. (a 1) p a 1 (mod p) Gemäss dem Binomischen Lehrsatz: p p p 1 p p k ( p 1)! p k p! a a 1 (a 1) p a p k a p p k 0 k k 0 k!( p k!) k 1 k!( p k!) p 1 ( p 1)! p k a p 0 (mod p) k 1 k!( p k!) p 1 ( p 1)! p k a 1 a 0 1 (mod p) (a 1) p a p p k 1 k!( p k!) Natürlich gibt es noch viele weitere Sätze über Primzahlen (P.Ribenboim(2004), E.Landau(1909), etc.), diese hier jedoch aufzulisten würde den Rahmen dieser Arbeit jedoch bei weitem sprengen. 3 Unendliche Menge der Primzahlen 3.1 Beweis von Euklid Beweisidee: Es gibt unendlich viele Primzahlen falls die Folge der Primzahlen nicht endlich ist. Annahme: Primzahlenfolge Pn enthält sämtliche Primzahlen. Pn: p1 2 , p2 3 , p3 5 , p4 7 , …., p n 1. P ( p1 p2 p3 ... pn ) 1 2. p ist ein Primteiler von P P 1 (mod p x ) (für x r und x N 0 ) und P 0 (mod p x ) Seite 7 [email protected] p p x p ist eine weitere Primzahl aber p Pn Widerspruch! 3.1.1 Variante von H.Brocard(1915) Beweisidee: Wenn es unendlich viele Primzahlen gibt, genügt es zu zeigen, dass es für jede Zahl eine Primzahl gibt die grösser ist. 1. n N 2. M n!1 M 1 (mod x ) für ( x n und x N ) 3. M 0 (mod p) p>n 3.2 Beweis von Goldbach(1730) Beweisidee: Es genügt eine unendliche Folge von natürlichen Zahlen zu finden, die ausser 1 keinen gemeinsamen Teiler haben. Da jede Zahl durch eine verschiedenen Primzahl teilbar sein müsste, ergibt sich so die Existenz von unendlich vielen Primzahlen. ( Fn 2 2 1 (für n N 0 ) (ggT ( Fa , Fb ) = 1) n (vgl. Fermatzahlen 5.1). 3.3 Beweis von Euler Beweisidee: Ein bestimmter aus allen Primzahlen gebildeter Ausdruck wird unendlich gross. p sei eine Primzahl 1 p n 0 n 1 1 1 1 1 1 2 .... n ist eine geometrische Reihe mit q 1 0 p p p p p 1 konvergiert mit dem Grenzwert:= 1 q sei eine andere Primzahl n 0 n 0 1 q n 1 p 1 1 1 q 1 1 1 1 1 1 1 1 .... n n 1 1 p n n 0 q n p 0 q 0 p 0 q 1 p 0 q 2 p q 1 1 p q Seite 8 [email protected] Die linke Seite entspricht der Summe der Kehrwerte aller natürlichen Zahlen der Form p n q m (n 0, k 0) , wobei jede der Zahlen nur einmal vorkommt, da jede der Zahlen eine eindeutige Primfaktorenzerlegung besitzt. Annahme es gibt genau r Primzahlen: r i 1 n 0 1 1 n pi i 1 1 1 pi r Die linke Seite entspricht daher der Summe der Kehrwerte aller möglichen Primfaktorenzerlegungen der r Primzahlen. Und da jede Primfaktoren Zerlegung eine eindeutige natürliche Zahl gibt, somit der Summe der Kehrwerte aller natürlichen Zahlen! r 1 1 1 divergiert die linke Seite, da ( r divergiert, falls r 1 ) 1 n 1 n n 1 n i 1 1 pi Die rechte Seite hingegen konvergiert mit einem endlichen Grenzwert, da sich mit jedem Glied der weitere Faktor immer stärker 1 annähert. 1 1 i 1 1 pi n 2 * 3 * 5 * 7 * 11 * 13 * .... * p n 1 2 4 6 10 12 pn 1 =Grenzwert(links) (Grenzwert rechts)=q ( q Q ) Widerspruch! Natürlich gibt es noch viele weitere Beweise der Unendlichkeit der Primzahlmenge (E.Kummer(1878), A.Tue(1897), H Furstenberg (1955), etc), sie hier jedoch alle Aufzulisten, würde den Rahmen meiner Arbeit bei weitem sprengen. 4 Wie erkennt man Primzahlen 4.1 Einfache Zerlegung Die einfachste (aber teilweise sehr lange dauernde) Methode zu testen, ob eine Zahl eine Primzahl ist, ist sie durch kleinere Primzahlen zu teilen, bis klar ist, dass es ausser Eins und sich selbst keinen Teiler gibt. Seite 9 [email protected] z.B: Ist 67 eine Primzahl? Dividend geteilt durch Divisor ergibt Quotient 67 : 1 = 67 67 67 67 67 67 67 67 67 67 67 67 67 67 67 67 67 : : : : : : : : : : : : : : : : 2 3 4 5 7 11 13 17 23 31 37 41 43 47 53 59 = = = = = = = = = = = = = = = = 33.50 22.33 16.75 13.40 9.57 6.09 5.15 3.94 2.91 2.16 1.81 1.63 1.56 1.43 1.26 1.14 Wie man in der Tabelle sehr schön sieht, ist es bewiesen, dass 67 eine Primzahl ist, sobald der Divisor grösser wird als der Quotient. Alle nun folgenden Quotienten sind kleiner als die bereits getesteten Divisoren. Durch das Assoziativgesetz kann man Quotient und Divisor auch tauschen, daher ist bewiesen, dass 67 keine Primzahl ist. Eine andere Formulierung für den gleichen Sachverhalt ist, dass man die Primteiler bis zur Wurzel der gesuchten Zahl testen muss. N ist eine Primzahl falls ggT ( N , p) 1 für p P und p N 4.1.1 Teilbarkeitsregeln Durch die Teilbarkeitsregeln, kann bei grösseren Zahlen sehr schnell und mit kleinem Rechenaufwand überprüft werden, ob sie durch eine bestimmte Primzahl teilbar sind. Eine Zahl ist durch 2 teilbar, wenn ihre letzte Ziffer durch 2 teilbar ist. Eine Zahl ist durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist. Eine Zahl ist durch 4 teilbar, wenn die Zahl, die aus ihren letzten beiden Ziffern gebildet wird, durch 4 teilbar ist. Eine Zahl ist durch 5 teilbar, wenn ihre letzte Ziffer durch 5 teilbar ist. Eine Zahl ist durch 6 teilbar, wenn sie durch 2 teilbar UND wenn ihre Quersumme durch 3 teilbar ist. Eine Zahl ist durch 7 teilbar, wenn ihre alternierende 3er-Quersumme durch 7 teilbar ist. Eine Zahl ist durch 8 teilbar, wenn die Zahl, die aus ihren letzten drei Ziffern gebildet wird, durch 8 teilbar ist. Eine Zahl ist durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist. Eine Zahl ist durch 10 teilbar, wenn ihre letzte Ziffer eine 0 ist. Eine Zahl ist durch 11 teilbar genau dann, wenn ihre alternierende Quersumme durch 11 teilbar ist. Eine Zahl ist durch 13 teilbar, wenn ihre alternierende 3er-Quersumme durch 13 teilbar ist. Seite 10 [email protected] Eine Zahl ist durch 17 teilbar, wenn ihre alternierende 8er-Quersumme durch 17 teilbar ist. Eine Zahl ist durch 19 teilbar, wenn ihre alternierende 9er-Quersumme durch 19 teilbar ist. Eine Zahl ist durch 27 teilbar, wenn ihre 3er-Quersumme durch 27 teilbar ist. 4.1.1.1 Beweise der Regeln Regeln, die auf der Teilbarkeit der aus den letzten Ziffern gebildete Zahl einer Zahl beruhen (2,4,5,8,10,etc) Jede beliebige ganze Zahl im Dezimalsystem ist als Summe ihrer 10er Potenzen schreibbar: .... 10 4 * ZT 10 3 * T 10 2 * H 101 * Z 10 0 * E ... 10'000ZT 1000T 100 H 10Z E E (mod 2) resp. (mod 5) etc. ... 10'000ZT 1000T 100H 10Z E ... 10'000ZT 1000T 100H 10Z E 10Z E (mod 4) resp. (mod 10) ... 10'000ZT 1000T 100H 10Z E 100H 10Z E (mod 8) Regeln, die auf der Teilbarkeit der Quersumme einer Zahl beruhen. .... 10 4 * ZT 10 3 * T 10 2 * H 101 * Z 10 0 * E ... 10'000ZT 1000T 100 H 10Z E ... 10'000ZT 1000T 100H 10Z E ZT+T+H+E (mod 3) bzw (mod 9) ... 10'000ZT 1000T 100H 10Z E -ZT+T-H+E (mod 11) .... (108 T 10 7 ZT 10 6 ZT ) (10 5 T 10 4 ZT 10 3 T ) (10 2 H 101 Z E ) .... 10 6 (10 2 T 101 ZT ZT ) 10 3 (10 2 T 101 ZT T ) 1(10 2 H 101 Z E ) .... 1(10 2 T 101 ZT ZT ) 1(10 2 T 101 ZT T ) 1(10 2 H 101 Z E ) (mod 7) + (mod 13) Die restlichen Regeln 17, 19, 27 lassen sich analog herleiten, wobei jedoch jeweils eine andere 10er-Potenz geteilt durch (17,19,27) den Rest 1 bzw den Rest -1 ergibt. 4.2 Sieb des Eratosthenes 1 Eine ergiebige Methode die auf einer grafischen Darstellung der einfachen Zerlegung fusst war bereits den Alten Griechen bekannt (Eratothenes (282 -202 v.Chr). Zuerst werden alle Zahlen bis zu der Zahl die man testen will, tabellarisch aufgeschrieben. Danach beginnt man mit der kleinsten Primzahl (p=2) und färbt die Felder aller Vielfachen dieser Zahl an. Dann wiederholt man diesen Schritt für alle Vielfachen der nächsten Zahl, die noch nicht angefärbt ist. Die nicht angefärbten Zahlen die am Schluss übrig bleiben sind Primzahlen.(Figur 1) 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Seite 11 Figur 1: Sieb des Erathotenes (1-100) (Schwarze Felder enthalten Primzahlen) [email protected] Das Titelbild meiner Arbeit zeigt die gesiebten Zahlen von 1-1000, stark vereinfachend ist, dass alle Reihen auf Parallelen liegen. 4.3 Test mit dem kleinen Lehrsatz von Fermat Der Satz von Fermat schien ebenfalls ein idealer Kandidat zu sein um mögliche Primzahlen zu finden, allerdings, stimmt die Umkehrung des Satzes nicht. Es gibt zerlegbare N, die die Bedingung: erfüllen, daher muss der Satz wie folgt ergänzt werden. Falls eine Zahl folgende zwei Bedingungen erfüllt ist sie eine Primzahl I. a N 1 1 II. a m 1 (mod N ) (für m=1,2,3, … N-2) oder ggT ( N , a) 1 (für m=1,2,3, … N-1) Allerdings ist in der Praxis dieser Test zu aufwendig, um grosse Primzahlen zu finden. Da er N-2 Operationen benötigt um zu überprüfen, ob eine gefundene Zahl auch wirklich eine Primzahl ist. 4.4 Agrawal-Kayal-Saxena-Primzahltest(2004) 2004 sorgten Agrawal, Kayal und Saxena, mit dem derzeit neusten Algorithmus (Figur 2) um zu testen, ob eine Zahl eine Primzahl ist für aufsehen. Das spezielle an diesem Test ist, dass er es vermag von Rechnern in überschaubarer (polynomieller) Zeit gelöst zu werden und dass er von einem bewiesenen Lemma zur Überprüfung von Primzahlen ausgeht. (Figur 2: AKS-Algorithmus) Dieser Algorithmus fusst somit auf einem sehr ähnlichen Satz wie dem Lehrsatz von Fermat. ( x a) N x N a (mod( x r 1, N ) für (1<a< ( 2 (r ) log N ). Hat jedoch den Vorteil, dass man den Test nicht mehr von 1 bis N durchführen muss, sondern nur noch im Bereich von 1 bis ungefähr log (N) mal durchführen muss, also ist er in Polynomialzeit lösbar. Die bedeutet, dass es sich um ein mit sequentiellen Computern praktisch lösbares Problem handelt, da die Rechenzeit mit der Problemgrösse maximal mit einer Polynomfunktion wächst. 4.4.1 Beweis des Lemmas (Analog zum kleinen Lehrsatz von Fermat): ( x a) p x p a (mod p) (für p = Primzahl) Seite 12 [email protected] p 1 ( p 1)! p k k x a a p x p 0 a p x p a (da a p a (mod p) ) ( x a) p x p p k 1 k!( p k!) Der vollständige Beweis dieses Testes würde den Rahmen dieser Arbeit bei weitem übersteigen und wurde 2004 von M.Agrawal et all. erbracht. 5 Besondere Arten von „Primzahlen“ 5.1 Fermatzahlen ( Fn 2 2 n 1 n 0) Fermat vermutete 1637, dass alle Fermatzahlen ( 2 2 1 ) Primzahlen sind. n F0 (22 1) 3 , F1 (22 1) 5 , F2 (22 1) 17 , F3 (22 1) 257 und 0 1 3 2 F4 (22 1) 65537 , F5 (22 1) 4'294'967'297 5 4 1732 widerlegte Euler diese Vermutung jedoch, in dem er mit 641 einen Teiler von F5 fand. Bis heute ist nicht bewiesen wie viele Fermatprimzahlen es gibt, jedoch ist die Wahrscheinlichkeit sehr klein, dass es noch eine weitere Fermatprimzahl gibt. 5.1.1 Eigenschaften von Fermatzahlen Annahme1: Fn ( F0 F1 F2 ... Fn1 ) 2 1. F1 F0 2 22 1 22 1 2 1 22 1 2 1 2 4 1 2 1 2 55 1 0 2. Fn1 F0 F1 F2 ... Fn 2 Fn 2 F0 F1 F2 ... Fn1 Fn ( F0 F1 F2 ... Fn1 ) 2 Fn1 ( Fn 2) Fn 2 Fn1 ( Fn ) 2 2Fn 2 (2 2 1) 2 2(2 2 1) 2 (2 2 ) 2 2(2 2 ) 1 2(2 2 ) 2 (2 2 ) 2 n 22 n 1 ( 2 2 ) 2 2 2 2 2 2 n n n n n n 1 Fermatzahlen haben keine gemeinsamen Teiler oder ggT ( Fn , Fa ) 1 Annahme2: ggT ( Fn , Fa ) p (für a n, a N ) Fn 2 F0 F1 F2 ... Fn1 ( Fn 2) 0 (mod Fa ) wobei Fa ein Teiler von Fn 2 ist. Seite 13 n n [email protected] ( Fn 2) 0 (mod p) da Fa Teiler von Fn 2 ist und p Teiler von Fa ist.) ggT ( Fn 2, Fn ) p p=2 Fa 0 (mod 2) 2 2 1 0 1 1 (mod 2) ( Fa ist ungerade!) Widerspruch! a 5.2 Mersenne-Primzahlen( M p 2 p 1 ) für pP M 2 2 2 1 3 , M 3 2 3 1 7 , M 4 2 4 1 15 , M 5 2 5 1 31 , M 7 2 7 1 127 Der Mönch Marin Mersenne (1588-1648) behauptete, dass für p=2,3,5,7,13,17,19,31,67,127 sowie 257 Mp Primzahlen sind. Frank Cole widerlegte 1903, dass M67 eine Primzahl ist und 1932 wurde mit einer frühen Rechenmaschine gezeigt, dass auch M257 teilbar ist. 5.2.1 Eigenschaften von Mersenne-Primzahlen Wenn Mp eine Primzahl ist, dann muss auch p eine Primzahl sein. Beweis durch Negation: Annahme: Wenn Mn keine Primzahl ist, dann ist auch n keine Primzahl sein. b 2 ab 1 (2 a 1)( 2 a (b 1) 2 a (b 2) .... 2 a 1) (2 a 1) 2 a (b i ) für a, b, i N i 1 (2 1) ist zerlegbar daher gilt falls (2 1) P ist auch p P ! ab p 5.3 Pseudoprimzahlen Pseudoprimzahlen sind Primzahlen die von einem der vielen Primzahl suchenden Algorithmen, fälschlicherweise für Primzahlen gehalten werden (z.B Fermatsche Pseudoprimzahlen, sind Nicht-Primzahlen, welche die Bedingung des kleinen Satzes von Fermat erfüllen.) 5.4 Primzahlzwilinge Primzahlzwillinge nennt man zwei Primzahlen die ein Differenz von 1 haben. (z.B 3,5 oder 5,7 oder 599, 601, etc.) 5.4.1 Eigenschaften von Primzahlzwillingen Alle Primzahlzwilinge ausser 3,5, kann man in der Form 6n-1 bzw. 6n+1 darstellen. Seite 14 [email protected] (6n 1)(6n 1) 1 36n 2 Es ist unbekannt, ob es unendlich Primzahlzwillinge gibt. 5.5 Primzahlvierlinge Primzahlvierlinge heissen Primzahlen der Form p, p+2, p+6, p+8. (z.B: 5, 7, 11, 13 oder 11,13,17,19 oder 821,823,827,829 etc.) 5.5.1 Eigenschaften von Primzahlvierlingen Alle Primzahlvierlinge mit Ausnahme von 5,7,11,13 lassen sich auch als (15n-4, 15n-2, 15n+2, 15n+4) darstelllen. ( (15n 4) (15n 2) (15n 2) (15n 4) 60n Es ist unbekannt ob es unendlich Primzahlvierlinge gibt. 5.6 Primzahlsechslinge Primzahlvierlinge heissen Primzahlen der Form p, p+4, p+6, p+10, p+12, p+14. (z.B: 7,11,13,17,19,23 oder 97,101,103,107,109,113 oder 16057,16061,16067,16069,16073) 5.6.1 Eigenschaften von Primzahlsechslingen (15n 8) (15n 4) (15n 2) (15n 2) (15n 4) (15n 8) 90n Primzahlsechlinge enthalten immer einen Primzahlvierling! Ob es unendlich viele Primzahlsechslinge gibt, ist unbekannt. 6 Primzahlrekorde 7 Bedeutung der Primzahlen 7.1 Histortische Bedeutung Primzahlen sind quasi die Delphine(flagship species) in der Mathematik, kaum ein Thema hat über Jahre so viele Mathematiker und Laien beschäftig. Für kaum ein Teilgebiet der Mathematik sind und waren so viele Prämien ausgesetzt. So sind aktuell von der Electronic Frontier Foundation 100'000 Dollar ausgesetzt für die erste Primzahl mit mehr als 10 Millionen Dezimalstellen. Seite 15 [email protected] Der britische Verlag Faber & Faber hatte im Jahre 2000 eine Belohnung von 1'000'000 Dollar ausgesetzt für einen Beweis der Goldbach Vermutung, die Frist ist aber leider bereits im April 2002 verstrichen. Innerhalb von zwei Wochen wurde die Korrektheit des AKS-Primzahltests bestätigt und die Homepage hatte über 2'000'000 Besucher in der ersten Woche. Daher sind für mich die Primzahlen, abgesehen von ihren zwei anderen Bedeutungen die Spielzeuge der Mathematiker oder wenn man so will eines der letzten grossen Rätsel aus dem Beginn der Mathematik. 7.2 Mathematische Bedeutung: Fundamentalsatz der Arithmetik Durch den Fundamentalsatz der Arithmetik sind Primzahlen so etwas wie die Atome der Arithmetik. 7.2.1 Definition Jede natürliche Zahl grösser eins, besitzt eine Primfaktorenzerlegung, die bis auf die Reihenfolge der Faktoren eindeutig ist! 7.2.2 Beweis Zerlegbarkeit: Annahme: N ist die kleinste Zahl, die nicht durch Primfaktoren zerlegbar ist. n ab (für 1<a<n) 1 b n n a Da n jedoch die kleinste Zahl ist, die nicht durch Primfaktoren dargestellt werden kann, sind a und b in Primfaktoren zerlegbar und somit ist auch deren Produkt n in Primfaktoren zerlegbar Widerspruch! Eindeutigkeit: Annahme: Die kleinste Zahl mit Primfaktoren Zerlegung ist k. k pl und k qu wobei ggT (u,p)=1 und ggT(l,q)=1 k ' k pu pl pu p(l u ) ggT(k' , p) 1 k ' k pu qu pu u (q p) ggT(u(q - p), p) 1 aber ggT(u,p)=1 ggT((q - p), p) 1 (q p) hp q hp p p(h 1) q ist zerlegbar und daher keine Primzahl Widerspruch! 7.3 Kryptografie: Praktische Anwendung der Primzahlen Seite 16 [email protected] Obwohl Primzahlen schon bei den Alten Griechen wohlbekannt und beliebt waren, ging es bis ins Jahr 1977 bis Primzahlen auch einen nutzen jenseits der Theorie fanden. Da es mit heutigen Mitteln sehr lange dauert eine grosse Zahl in ihre Primfaktoren zu zerlegen, ist das erzeugen einer grossen Zahl durch das multiplizieren zweier Primfaktoren sehr einfach. Auf diesem Prinzip funktioniert das RSA –Kryptosystem (Rivest, Shamir und Adleman(1977)). Bei vielen herkömmlichen Kryptografiesystemen wurden Daten mit einem geheimen Schlüssel verschlüsselt. Der Austausch dieses Schlüssel stellte ein hohes Risiko dar, denn sobald eine Drittperson Kenntnisse des Schlüssels erhielt, waren die Daten nicht mehr sicher. Um dies zu umgehen wird der Schlüsselaustausch im RSA-System offen vorgenommen (puplic key). Entscheidend für die Entschlüsselung ist der zweite persönliche Schlüssel (private key) der, jedoch nur dem Empfänger nicht aber dem Absender bekannt ist. 1. Generation der Schlüssel n pq wobei p und q möglichst grosse Primzahlen sind. 1 s ( N ) (q 1)( p 1) für ggT ( s, ( N )) 1 ts 1 (mod ( N )) ts k (N ) =1 Wobei n, s die öffentlichen Schlüssel sind. Und p, q bzw. das daraus resultierende t der Privateschlüssel. Bsp: n pq 143 1113 ( N ) (143) ( p 1)( q 1) 10 12 120 ggT ( s, ( N )) 1 ggT (23,120) 1 ts k ( N ) 1 23t 120k 1 s=47 2. Verschlüsselung der Nachricht (Zahlenfolge) M mit öffentlichem Schlüssel M ' M s ( mod n) M=7 M ' 7 23 2 (mod 143) 3. Entschlüsslung mit privatem Schlüssel (M ' )t M st M (mod n) 223 7 (mod 143) In der Realität verschlüsselt man Texte natürlich nicht mit solch einfachen Zahlen, sondern es wird empfohlen über 200 Stellen grosse Zahlen zu gebrauchen für diese ist es mit heutigen Computern nicht möglich die Sicherheit zu knacken. Da RSA im Vergleich zu anderen Verfahren (ohne öffentliche Schlüssel) um mindestens einen Faktoren 1000 langsamer ist, wird es oft nur benutzt um einen Schlüssel sicher auszutauschen. 8 Primzahlen in der Schule Sek1-Inputs Seite 17 [email protected] 8.1 Primzahlen als Hauptthema Wie ich in der historischen Bedeutung erläutert habe, sind für mich die Primzahlen so etwas wie die Delphine der Mathematik. Wenn man daher das Thema mit Schülern und Schülerinnen behandelt, finde ich es wichtig den Spassfaktor möglichst im Vordergrund zu halten. 8.1.1 Aufgaben im Rekord-Stil (am besten mit kleiner Belohnung z.B: Tafel Schoggi) A) Ohne Vorwissen: Wer findet als erster eine Zahl mit nur zwei Teilern über 100 (bzw. 1000 (Binnendifferenzierung)). B) Vertiefung: Wer findet als erstes ein Primzahlzwilling über 100 oder welches Team findet innerhalb einer Schulstunde den höchsten Primzahlzwilling. Etc. 8.1.2 Aufgaben im Internet A) Wie heisst die grösste derzeit bekannte Primzahl. B) Finde eine interaktive Darstellung des Siebes von Erasthothenes. C) Teilbarkeitsregeln D) Primzahltabellen E) Primzahlzähler Etc. 8.1.3 Aufgaben mit Teilbarkeitsregeln A) Finde aus einer Zahlengruppe (z.B 10 Zahlen) die Primzahlen heraus. B) Erstellt selbst Zahlengruppen mit Primzahlen. Etc. 8.1.4 Sieb von Erathosthenes A) Sieb des Erathosthenes Anleitung, mit kurzer Geschichte Eratosthenes (Fachübergreifend) B) Siebe alle Zahlen bis 100, was fällt auf? C) Konstruktionsaufgabe bis 1000 mit Parallelverschiebung der Teiler. D) Jeder färbt auf einer Tabelle (Klarsichtfolie) alle Vielfachen einer Primzahl an. (Binnendifferenzierung. Schwache Schüler und Schülerinnen bekommen einfache Teiler) Am Schluss werden die Folien Stück für Stück auf den Hellraumprojektorgelegt und alle durchsichtig bleibenden Zahlen sind Primzahlen. Etc. 8.1.5 Einfache Primzahlbeweise A) Die Beweise von Euklid und Brokhard verstehen Seite 18 [email protected] B) Unbewiesene Sätze überprüfen für den Raum 1-100 (z.B Goldbach Vermutung). etc. 360 8.1.6 Primfaktorenzerlegung 120 A) Zerlegung einer Zahl in ihre Primfaktoren B) Primfaktorenzerlegung als Baum(Figur 3). 60 15 5 8.2 Primzahlen in Neben-Themen 360 3 90 2 30 4 3 2 4 10 3 5 2 2 3 2 2 (Figur3: eindeutige Primfaktorenzerlegung als Baum) 8.2.1 Kürzen und Erweitern A) Um einen Bruch in einem Schritt korrekt zu Kürzen, zerlegt man beide Nenner in ihre Primfaktoren und bildet den ggT der beiden Nenner. B) Um einen Bruch in einem Schritt korrekt zu erweitern, zerlegt man beide Nenner in ihre Primfaktoren und bildet das kgV der beiden Nenner. 8.2.2 Parallelverschiebung Das Sieb des Erathosthenes ist sehr gut geeignet für eine Parallelverschiebungsübung. Der Lehrer verteilt einen Ausdruck der Zahlen 1-1000, in der der Mittelpunkt jedes Feldes durch einen Punkt gekennzeichnet ist. Die Schüler und Schülerinnen finden nun durch die Parallele-Verschiebung der jeweiligen Zahlen-Reihen, alle Teiler der Ursprungsprimzahl. (vgl. Titelbild dieser Arbeit). 8.2.3 Beweise Die Beweis für die unendliche Menge der Primzahlen von Euklid und Brokhard sind einfach nachzuvollziehende Beweise. 8.2.4 Repetition der Reihen Anhand der Primzahlen von 1-100 können im mündlichen Rechnen sehr gut die Reihen repetiert werden. Ist 63 eine Primzahl, nein sie geht durch 7 und 9 und 3 etc. 8.3 Primzahlen in Fachübergreifenden Themen / Themen für Projektarbeiten und Projektwochen Seite 19 [email protected] 8.3.1 Mathematiker und ihre Beweise(Geschichte, Mathematik) Hier könnte man unter dem Stichwort: griechische Mathematiker (Euklid, Eratosthenes, Pythagoras, Thales, Appollonios, Archimedes, Aristarchos von Samos, etc). Natürliche wäre das gleiche auch mit modernen Mathematikern möglich(Euler, Goldbach, etc)! 8.3.2 Krypografie (Geschichte, Mathematik, Deutsch) Hier könnte man einen Text nach dem RSA –Verfahren verschlüsseln….allerdings bräuchte man dafür auf dem Internet einen Algorithmus der Kongruenzen ausrechnen kann. 8.3.3 Krypografie (Geschichte, Mathematik, Deutsch) Hier könnte man einen Text nach dem RSA –Verfahren verschlüsseln….allerdings bräuchte man dafür auf dem Internet einen Algorithmus der Kongruenzen ausrechnen kann oder irgend ein Mathematikprogramm. 8.3.4 Primzahlen auf dem Internet (Mathematik, Informatik) Hier sind die Möglichkeiten beinahe grenzenlos, da Primzahlen die Delphine der Mathematik sind, wimmelt es im Internet nur so von Informationen über sie. Daher sind internetRecherchen ebenso ergiebig, wie das Programmieren einfacher Algorithmen etc. 9 Glossar Polinominalzeit Seite 20 [email protected] 10 Quellen und Links H.Brocard(1915) Goldbach(1730) (E.Kummer(1878), A.Tue(1897), H Furstenberg (1955), (P.Ribenboim(2004), E.Landau(1909), etc.) Tomás Oliveira e Silva (2005) (vgl. Wikibook: „Warum_1_keine_Primzahl_ist!“) H. Brocard (1915) un preuve simple Intermédiare des Mathématiciens 22, p 253 Goldbach(1730) Briefwechsel mit Euler im Juli M Agrawal, N Kayal, N Saxena (2004) Primes in P Indian Institute of Technology, Kanpur http://www.cse.iitk.ac.in/users/manindra/algebra/primality.pdf (Rivest, Shamir und Adleman(1977)) RSA paper muss ich noch suchen http://www.anderegg-web.ch/phil/eratosthenes.htm Erasthotenes http://www.faust.fr.bw.schule.de/mhb/eratosib.htm Sien des E Seite 21











