Leistungskurs 13.1, Jg. 98/99, HhG

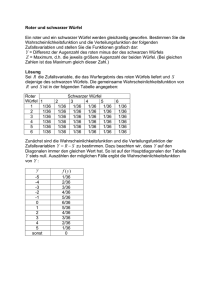
2004/05 , 13.1 , LK Mathematik
Bonn, den 21. Januar 2005
Übungsaufgaben Nr. 9
1. Ein Hexaederwürfel trage auf vier Seiten die 2 und auf zwei Seiten die 5.
(a) X sei die Augenzahl beim einmaligen Würfeln. Man bestimme die Wahrscheinlichkeitsverteilung
von X und berechne Erwartungswert und Varianz.
(b) Der Würfel wird so lange geworfen, bis die Augensumme wenigstens 7 beträgt. Man zeichne ein
Baumdiagramm für diesen stochastischen Prozeß. Z sei die Anzahl der benötigten Würfe. Man
bestimme Verteilung und Erwartungswert von Z
(c) Der Würfel werde acht mal geworfen. Wieviel verschiedene Wurffolgen sind möglich ? Welche
Werte kann die Augensumme Y der acht Würfe annehmen ? Man berechne P(Y = 25) Man berechne ferner E(Y) mit Hilfe von Sätzen über Erwartungswerte.
(d) Um zu prüfen, ob der verwendete Würfel "gut" ist, wird er 1800 mal geworfen. N sei die Anzahl
der geworfenen Fünfer. In welchem Intervall liegt N mit Wahrscheinlichkeit 95 %, wenn der
Würfel tatsächlich gut ist ?
(e) Zwei Spieler machen eine Wette. A besitzt einen gewöhnlichen Würfel, B den bisher untersuchten. Beide sind gut. Jeder würfelt mit seinem Würfel. A gewinnt, wenn er eine höhere Augenzahl
als B hat, sonst gewinnt B. Welche Gewinnwahrscheinlichkeit haben A und B ?
2. Ein Würfel, der zwei Zweien, zwei Vieren und zwei Sechsen trägt, wird 69 mal geworfen.
(a) Welchen Erwartungswert hat die Anzahl der Sechsen ? Mit welcher Wahrscheinlichkeit tritt dieser Erwartungswert genau ein ? Man berechne diesen Wert exakt mit Hilfe der Binomialverteilung sowie näherungsweise mit Hilfe von  und .
(b) Dieselbe Fragestellung soll für 70 Würfe und die Zahl von 22, 23 und 24 Würfen bearbeitet werden, wobei Sie die entsprechenden Terme der Binomialverteilung durch Rekursion aus dem Ergebnis von (a) ermitteln sollen (Werte „sprengen“ den TR).
3. Stetige Zufallsvariable
Eine Zufallsvariable habe die Dichtefunktion
f(x) = C.x.(2 - x), x  [0 ; 2]
(a) Man berechne die kumulative Verteilungsfunktion F(x).
(b) Man berechne den Erwartungswert dieser Zufallsvariablen.
(c) Die Varianz einer stetigen Zufallsvariablen ist genau wie bei diskreten Zufallsvariablen
Var (X) = ² = E(X - )²
Man berechne die Varianz der gegebenen Zufallsvariablen und überprüfe am konkreten Fall die
Gültigkeit der Formel
Var (X) = E(X²) - ²
Man beweise diese Formel anschließend allgemein.
4. Kühnes Spiel
Ich habe 1 DM brauche dringend (a) 6 DM, (b) 7 DM, (c) 9 DM. Ich versuche, mein Ziel in einem gerechten Glücksspiel durch kühne Strategie zu erreichen. Man zeichne den Graphen des Spiels und
errechne Gewinnwahrscheinlichkeit und mittleren Gewinn.
5. Wie lange dauert es im Mittel, bis man mit einem gewöhnlichen Würfel zweimal hintereinander eine
6 wirft. Man verallgemeinere die Aufgabenstellung auf ein Ereignis, das mit Wahrscheinlichkeit p
einmal eintritt.