K12 GK Physik 2pas2 1 - Hans-Carossa

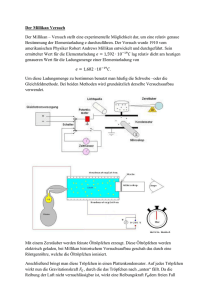
K12
GK Physik
2pas2
1. Klausur
29.1.2007
Allgemeine Hinweise:
Die Rechenaufgaben sind nach folgendem Schema durchzuführen:
 Gegeben, Gesucht
 Lösung
(Allgemeiner Ansatz, Auflösen nach der gesuchten Größe,
Einsetzen mit Benennungen, Ergebnis)
 Antwort (Kurzantwort) unter Beachtung der jeweils geltenden Ziffern
Die äußere Form der Arbeit kann mitbewertet werden.
1)
Arbeitszeit:
75 Minuten
Kräfte im elektrischen Feld
5
a) Erklären Sie genau (mit Skizze und präzisem Text mit Fachbegriffen) folgende Beobachtung:
Eine auf einer Tischplatte liegende, ungeladene (!) Watteflocke wird von der (positiv) geladenen
Kugel des Bandgenerators angezogen.
2
b) Skizzieren Sie (ohne weitere Erklärung) einen zu a) analogen magnetischen Vorgang
3) Das Experiment von Robert Andrews Millikan
Im Jahre 1923 erhielt Robert Andrews Millikan den Nobelpreis für den Nachweis und die
Bestimmung der Elementarladung.
4
a) Skizzieren Sie das Prinzip der Versuchsanordnung der Schwebemethode und tragen Sie in die
Zeichnung die auf ein negativ geladenes Öltröpfchen wirkenden Kräfte sowie die Richtung des
elektrischen Feldes ein.
9
b) Berechnen Sie, wie viele Überschusselektronen sich auf einem negativ geladenen, schwebenden,
kugelförmigen Öltröpfchen befinden, wenn dessen Radius 5,0  10 5 cm , die Dichte des Öls
g
 Öl = 9,0  10 2
, und die Kondensatorspannung 58 V bei einem Plattenabstand von 6,0 mm
dm 3
betragen.
3
c) Mit dieser Schwebemethode sind zwei grundsätzliche messtechnische Probleme verbunden.
Benennen Sie diese und geben Sie für eines dieser Probleme die physikalische Ursache an.
 Fortsetzung auf Seite 2 !
y
4) Elektronen in elektrischen Feldern
Elektronen werden durch die
Beschleunigungsspannung Ua von der
Ruhelage auf 5,0 % der Lichtgeschwindigkeit beschleunigt. Es ist:
U’ = 85 V; s = 2,0 dm ; d’ = 4,0 cm.
P
U’
’
B
d’
x
Ua
4
a) Berechnen Sie den Wert der
Beschleunigungsspannung Ua.
4
b) Zeigen Sie, dass sich die Querbeschleunigung ay im Bereich des Ablenkkondensators nach
e U '
m
der Formel ay =
ergibt und berechnen Sie den Wert von ay. [ 3,7  1014 s 2 ]
m  d'
6
c) Berechnen Sie, welche Spannung man höchstens an den Ablenkkondensator legen darf, um
sicherzustellen, dass die Elektronen den Bereich des Ablenkkondensators auf jeden Fall verlassen
können (ohne vorher auf eine der Kondensatorplatten zu treffen).
4
d) Wie ändert sich die Ladung Q der Platten des Ablenkkondensators, wenn der Plattenabstand bei
angeschlossener Spannungsquelle verdoppelt wird? Begründen Sie Ihre Antwort.
s
q
5) „Das Erdmagnetfeld ist schuld“ (??)
Beim Bruch einer Hochspannungsleitung auf der Nordhalbkugel der Erde
versucht sich der verantwortliche Ingenieur auf die Kraft auf stromdurchflossene
Leiter im magnetischen Feld der Erde herauszureden. Als Sachverständige(r) der
Physik sollen Sie über diese Ausrede befinden. (Daten am Ende dieser Aufgabe)
6
a) Berechnen bzw. ermitteln Sie Betrag und Richtung der auf die Hochspannungsleitung wirkenden
Lorentzkraft.
3
b) Vergleichen Sie diese Lorentzkraft mit der Gewichtskraft der Leitung und geben Sie Ihr Urteil ab.
Daten:
50
Länge der Leitung zwischen 2 Hochspannungsmasten: 200 m
Stromstärke in jeder Leitung: 400 A, Gleichstrom
Stromrichtung (technisch): von Ost nach West
Masse des 200 m langen Leitungskabels: 6,0 t
Flussdichte des Erdmagnetfeldes am Ort der Stromleitung: 40 T
Deklination des Erdmagnetfeldes am Ort der Stromleitung: 0o
Inklination des Erdmagnetfeldes am Ort der Stromleitung: 30o
(Inklinationswinkel = Winkel zwischen der Magnetfeldrichtung und der Horizontalen)
K12
GK Physik
2pas2
1. Klausur
29.1.2007
Allgemeine Hinweise:
Arbeitszeit:
75 Minuten
Die Rechenaufgaben sind nach folgendem Schema durchzuführen:
 Gegeben, Gesucht
 Lösung
(Allgemeiner Ansatz, Auflösen nach der gesuchten Größe,
Einsetzen mit Benennungen, Ergebnis)
 Antwort (Kurzantwort) unter Beachtung der jeweils geltenden Ziffern
Die äußere Form der Arbeit kann mitbewertet werden.
1) Kräfte im elektrischen Feld
5
a) Erklären Sie genau (mit Skizze und präzisem Text mit Fachbegriffen) folgende Beobachtung:
Eine auf einer Tischplatte liegende, ungeladene (!) Watteflocke wird von der (positiv) geladenen
Kugel des Bandgenerators angezogen.
2P:
+
+
„Elektrische Influenz in Nichtleitern“:
Watte befindet sich im elektr. Feld der Bandgeneratorkugel.
In den Molekülen der Wattefasern erfolgt Ladungstrennung durch Influenz. 1P
(Moleküle werden zu elektrischen Dipolen.)
Negative Influenzladungen sind näher an der Kugel als positive Influenzladungen. (vgl. Skizze)
Auf Grund der Inhomogenität des radialsymmetrischen Feldes folgt: 1P
Anziehung der neg. Influenzladungen > Abstoßung der positiven Influenzladungen. 1P
2
b)
Skizzieren Sie (ohne weitere Erklärung) einen zu a) analogen magnetischen Vorgang.
Eisenfeilspäne (Magnetnadeln, ...) werden in der Nähe des Pols eines Stabmagneten ausgerichtet
und von diesem angezogen.
3) Das Experiment von Robert Andrews Millikan
Im Jahre 1923 erhielt Robert Andrews Millikan den Nobelpreis für den Nachweis und die
Bestimmung der Elementarladung.
4
a) Skizzieren Sie das Prinzip der Versuchsanordnung der Schwebemethode und tragen Sie in die
Zeichnung die auf ein negativ geladenes Öltröpfchen wirkenden Kräfte sowie die Richtung des
elektrischen Feldes ein.
Prinzip der Versuchsanordnung: 2P
+
Kräfte: 1P
Feldrichtung: 1P
Fel
E
U
FG
9
b) Berechnen Sie, wie viele Überschusselektronen sich auf einem negativ geladenen, schwebenden,
kugelförmigen Öltröpfchen befinden, wenn dessen Radius 5,0  10 5 cm , die Dichte des Öls
g
 Öl = 9,0  10 2
, und die Kondensatorspannung 58 V bei einem Plattenabstand von 6,0 mm
dm 3
betragen.
geg.: r = 5,0  10 5 cm ;
 Öl = 9,0  10 2
g
;
dm 3
U = 58 V ;
d = 6,0 mm = 6,0  10 3 m
ges.: Anzahl der Überschusselektronen
Lös.:
Fel = FG ;
qE = mg ;
q
q
U
4 3
r g ;
= 
d
3
= 
4 3
d
r g 
=
3
U
= 9,0  10 2
=
3
kg 4
N 6,0  10 3 m
7

=


5
,
0

10
m

9
,
81
m3 3
58V
kg
4,8  10 19 C =


3,0  1,6  10 19 C
Antw.: Auf dem Öltröpfchen befinden sich 3 Überschusselektronen.
3
c) Mit dieser Schwebemethode sind zwei grundsätzliche messtechnische Probleme verbunden.
Benennen Sie diese und geben Sie für eines dieser Probleme die physikalische Ursache an.
Lös.: Probleme: Ermittlung des Tröpfchenradius
Einstellung des Gleichgewichtszustandes
Aufgrund der Brownschen Molekularbewegung führen alle Öltröpfchen völlig unregelmäßige
Zitterbewegungen aus, was zur Folge hat, dass sich der Gleichgewichtszustand nicht exakt
einstellen lässt.
4) Elektronen in elektrischen Feldern
y
Elektronen werden durch die
Beschleunigungsspannung Ua von der
Ruhelage auf 5,0 % der Lichtgeschwindigkeit beschleunigt. Es ist:
P
U’
’
B
d’
x
U’ = 85 V; s = 2,0 dm ; d’ = 4,0 cm.
Ua
Geg.:
4
m
m
v = 5,0 % = 0,05  c = 1,5  3,0  10
= 1,5  10 7
s
s
U’ = 85 V;
s = 2,0 dm = 0,20 m ; d’ = 4,0 cm = 0,040 m .
s
q
8
a) Berechnen Sie den Wert der Beschleunigungsspannung Ua.
ges.: Ua
Lös.: Epot = Ekin
eUa =
1
2
m v2

9,1  10 31 kg  1,5  10 7
mv²
Ua =
=
2e
2  1,6  10 19 C
= 639,84 V
4
m
s

2
=
= 6,3984  10 2 V
= 6,4  10 2 V =
0,64 kV
b) Zeigen Sie, dass sich die Querbeschleunigung ay im Bereich des Ablenkkondensators nach
e U '
m
der Formel ay =
ergibt und berechnen Sie den Wert von ay. [ 3,7  1014 s 2 ]
m  d'
Beh.: ay =
Bew.: ay =
e U '
m  d'
Fy
m
=
q  Ey
m
q U ' e U '
m
1,6  10 19 C  85V
=
=
=
= 3,7  1014 .
31
m d'
s²
m  d ' 9,1  10 kg  0,040m
6
c) Berechnen Sie, welche Spannung man höchstens an den Ablenkkondensator legen darf, um
sicherzustellen, dass die Elektronen den Bereich des Ablenkkondensators auf jeden Fall verlassen
können (ohne vorher auf eine der Kondensatorplatten zu treffen).
Lös.: y1 =
4
1
 ay t 2
2
2
1 e U '  s
d'

= 
2 m  d '  v x
2



d ' 2 m  v x
U’ =
e  s²
0,040m2  9,1  10 31 kg  1,5  10 7 ms 2
2
1,6  10 19 C  0,20m
2
=
= 51 V
d) Wie ändert sich die Ladung Q der Platten des Ablenkkondensators, wenn der Plattenabstand bei
angeschlossener Spannungsquelle verdoppelt wird? Begründen Sie Ihre Antwort.
Geg.:
U’ = konst und d’  2d’
Ges.:
Wie ändert sich Q?
Lös.:
Die Ladung Q auf den Platten des Ablenkkondensators ist nur noch halb so groß.
Begr.:
Q = CU
= C o 
A
wird halbiert.
d
5) „Das Erdmagnetfeld ist schuld“ (??)
Beim Bruch einer Hochspannungsleitung auf der Nordhalbkugel der Erde
versucht sich der verantwortliche Ingenieur auf die Kraft auf stromdurchflossene
Leiter im magnetischen Feld der Erde herauszureden. Als Sachverständige(r) der
Physik sollen Sie über diese Ausrede befinden. (Daten am Ende dieser Aufgabe)
Daten:
Länge der Leitung zwischen 2 Hochspannungsmasten: 200 m
Stromstärke in jeder Leitung: 400 A, Gleichstrom
Stromrichtung (technisch): von Ost nach West
Masse des 200 m langen Leitungskabels: 6,0 t
Flussdichte des Erdmagnetfeldes am Ort der Stromleitung: 40 T
Deklination des Erdmagnetfeldes am Ort der Stromleitung: 0o
Inklination des Erdmagnetfeldes am Ort der Stromleitung: 30o
(Inklinationswinkel = Winkel zwischen der Magnetfeldrichtung und der Horizontalen)
N
W
O
L = 200 m
I = 400 A,
I
m = 6,0 t = 6000 kg
B = 40 T
Inklinationswinkel = 30o
S
N
o
30
S
6
a) Berechnen bzw. ermitteln Sie Betrag und Richtung der auf die Hochspannungsleitung wirkenden
Lorentzkraft.
Lös.:

Richtung von FL:
Schaut man entlang der Stromleitung von O nach W:
I
Süden
Norden
B
FL
Die Lorentzkraftpfeil liegt in der durch die NS-Richtung und der Vertikalen aufgespannten
Ebene. Der Winkel zwischen FL und der NS-Richtung beträgt 60o .
Richtung von FL : „im Wesentlichen nach unten“

Betrag von FL:
B=
F
;  FL = B  I  l
I l
Da B  I  FL = 40  10 6 T  400 A  200m = 3,2 N
( cos 30o =
 FL,vert
3
Bhor
;  Bhor = B cos30o .
B
= Bhor  I  l = B cos30o  I  l = 40  10 6 T cos30o  400 A  200m = 2,8 N )
b) Vergleichen Sie diese Lorentzkraft mit der Gewichtskraft der Leitung und geben Sie Ihr Urteil ab.
FG = m g = 6000 kg  9,81
N
= 58860 N = 59 kN >> 2,8 N = FL
kg
Die Lorenzkraft ist gegenüber der Gewichtskraft betragsmäßig vernachlässigbar gering,
kann daher nicht als Grund für das Reißen des Seils angeführt werden.
„Der Ingenieur ist eine Flasche.“