Sangaku – Japanische Tempelgeometrie

Bayerische
Julius Maximilians-Universität
Würzburg
Erstes Staatsexamen für ein Lehramt an Realschulen
Schriftliche Hausarbeit
Thema:
„Sangaku – Japanische Tempelgeometrie“
Eingereicht von: Christiane Hartmann
Fach: Mathematik
Eingereicht am: 29.02.2008
Dozent: Prof. Dr. Jörn Steuding
1
Inhaltsverzeichnis:
1
Einführung ____________________________________________________ 3
2
Allgemeines ____________________________________________________ 5
3
Geschichtlicher Hintergrund ______________________________________ 8
3.1
Allgemeiner Überblick über die Geschichte der japanischen Mathematik __ 8
3.2
Die Renaissance der japanischen Mathematik _________________________ 9
3.3
Takakazu Seki Kowa _____________________________________________ 10
4
Die Geometrie in der Wasan- Mathematik __________________________ 12
4.1
Allgemeines_____________________________________________________ 12
4.2
Interessante Entdeckungen ________________________________________ 14
4.2.1
4.2.2
Das Malfatti- Problem _________________________________________________ 14
Das Casey Theorem ___________________________________________________ 17
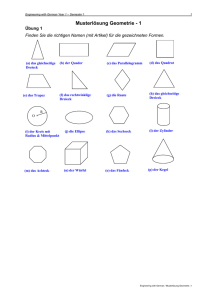
5 Wichtige Sätze, die häufig zur Lösung von Sangaku- Problemen benötigt
werden _________________________________________________________ 21
5.1
Der Satz des Pythagoras __________________________________________ 21
5.2
Sätze über Tangenten und Sekanten ________________________________ 22
5.3
Ähnlichkeitssätze ________________________________________________ 23
6
Einige Sangaku- Aufgaben ______________________________________ 25
6.1
Sangaku 1 ______________________________________________________ 25
6.2
Sangaku 2 ______________________________________________________ 27
6.3
Sangaku 3 ______________________________________________________ 29
6.4
Sangaku 4 ______________________________________________________ 32
6.5
Sangaku 5 ______________________________________________________ 35
7
Sangakus in der heutigen Schulgeometrie __________________________ 36
7.1
1. Beispiel aus dem Schulbuch _____________________________________ 36
7.2
2. Beispiel aus der Schulgeometrie __________________________________ 39
7.3
3. Beispiel aus dem Schulbuch _____________________________________ 41
7.4
Allgemeines zur Anwendung in der Schule ___________________________ 43
8
Vergleich mit der europäischen Geometrie zur Wasan- Zeit ____________ 44
8.1
Allgemeine Entwicklung der europäischen Geometrie _________________ 44
8.2
Die Inversions- Methode __________________________________________ 45
8.3
Der Satz von Descartes ___________________________________________ 45
8.3.1
8.3.2
9
10
Lösung im n-dimensionalen Fall _________________________________________ 46
Original japanische Lösung _____________________________________________ 50
Schlusswort ___________________________________________________ 59
Literaturverzeichnis __________________________________________ 60
2
1 Einführung
In dieser schriftlichen Hausarbeit beschäftige ich mich mit dem Thema Sangaku –
Japanische Tempelgeometrie, welche auch als Wasan bezeichnet wird.
Im ersten Teil meiner Arbeit gebe ich dem Leser zunächst einige allgemeine
Informationen zur Japanischen Tempelgeometrie und einen kurzen Überblick
darüber, was Sangakus sind und welchen Zweck sie erfüllen.
Das dritte Kapitel erläutert den geschichtlichen Hintergrund, der von großer
Bedeutung für die Entstehung der eigenständigen japanischen Wasan–Mathematik
ist. Hierbei gehe ich auch auf den wichtigsten japanischen Mathematiker dieser Zeit
ein, Takakazu Seki Kowa, der für seine Zeit erstaunliche mathematische
Entdeckungen gemacht hat.
Was man genau unter der Geometrie in der Wasan-Mathematik versteht, stelle ich im
vierten Kapitel dieser Arbeit dar.
Im fünften Kapitel werde ich einige mathematische Sätze kurz erklären, die häufig
zur Lösung von Sangaku-Problemen verwendet werden. Die meisten dieser Sätze
habe ich bei meinen Lösungsvorschlägen auch benutzt.
Im sechsten Kapitel meiner Arbeit werden schließlich einige Sangaku-Aufgaben
vorgestellt, zu denen ich Lösungsvorschläge mache. Dabei habe ich die Skizzen im
dynamischen Geometrieprogramm Dyna-Geo erstellt und in meine Arbeit eingefügt.
Das siebte Kapitel geht auf die Verwendung von Sangakus im Schulunterricht ein
und stellt einige Sangaku- ähnliche Schulbuchaufgaben vor.
Im achten Kapitel ziehe ich einen Vergleich zur europäischen Geometrie dieser Zeit,
indem ich zunächst allgemein die Entwicklung der europäischen Geometrie erläutere
und dann einige Unterschiede darlege.
Zu Beginn meiner Arbeit möchte ich noch erwähnen, dass es relativ schwierig war,
Literatur zu diesem Thema zu finden, da es zum einen fast nur japanische Texte dazu
gibt und zum anderen die japanische Tempelgeometrie einfach zu wenig bekannt ist
und es deshalb generell sehr wenig Literatur dazu gibt. Der Wissenschaftler, der sich
wohl bisher am meisten mit Wasan beschäftigt hat, ist Hidetosi Fukagawa, der auch
das Hauptwerk über die Japanische Tempelgeometrie, „Japanese Temple Geometry
Problems“, verfasst hat. Dieser japanische Mathematiker, der einen Doktortitel der
Mathematik
trägt,
widmete
zusammen
mit
seinem
amerikanischen
3
Wissenschaftskollegen, Mathematikprofessor Dan Pedoe der Erforschung der
japanischen Mathematik der Edo-Periode viel Zeit und Geduld und ihnen beiden ist
es wohl zu verdanken, dass dieses Thema in der westlichen Welt noch nicht völlig in
Vergessenheit geraten ist. In den wenigen Texten, die ich zu Wasan im Internet oder
auch in anderen Büchern und Zeitschriften gefunden habe, wird auf das Werk von
Fukagawa und Pedoe verwiesen und meist finden sich keine neuen SangakuProbleme, die nicht schon bei ihnen gelöst wurden.
4
2
Allgemeines
Sangaku ist das japanische Wort für kunstvoll verzierte Holztafeln, in die
geometrische Probleme eingraviert sind. Sie wurden vor allem zum Schmücken von
Decken von Schreinen und Tempeln aufgehängt. Diese Kunstwerke entstanden
während der nationalen Isolation Japans, in der so genannten Edo-Periode (16031867) in Japan. Die folgende Abbildung zeigt eine solche Sangaku-Tafel [C]:
Ein anderer Begriff, der in diesem Zusammenhang auch häufig zu finden ist, ist
„Wasan“, der die Mathematik der japanischen Tempelgeometrie im Allgemeinen
bezeichnet. In aller Kürze gesagt, enthalten diese Tafeln zahlreiche geometrische
Probleme, mit denen mathematisch interessierte Menschen aller Schichten
versuchten, sich gegenseitig zu beeindrucken und herauszufordern. Es wurde aber
auch als Zeichen der Verehrung oder Danksagung an inspirierende Geister und
Götter verwendet. Zunächst waren es wohl hauptsächlich gebildete Japaner der
Samurai-Klasse, die Sangaku-Tafeln erschufen, später beschäftigten sich Menschen
aller Klassen und jeden Alters mit den mathematischen Holztafeln.
In den Sangakus wird hauptsächlich die klassische euklidische Geometrie verwendet,
jedoch mit einer völlig anderen Motivation, als in der Schulmathematik oder der
europäischen Geometrie üblich. Die wichtigsten mathematischen Elemente der
japanischen Tempelgeometrie sind v.a. Kreise, Ellipsen und Dreiecke, die in den
verschiedensten Arten ineinander einbeschrieben sind und so Anlass für unzählig
5
verschiedene Aufgaben aller Schwierigkeitsstufen bilden. Die meisten Sangakus
erhalten mehrere Theoreme und nur Ergebnisse ohne Beweise. Außerdem findet sich
auf fast jeder Tafel der Hersteller und das Datum der Widmung [FuPe].
Zu erwähnen ist weiterhin, dass nicht jedes Sangaku geometrische Probleme
darstellt. Es werden zum Beispiel auch Aufgaben gestellt, bei denen die Volumina
von krummflächig begrenzten Körpern zu berechnen sind, wozu man eigentlich die
Infinitesimalrechnung benötigt, die aber zu dieser Zeit in Japan noch unbekannt war.
Außerdem wurden Tafeln mit diophantischen Problemstellungen gefunden, also
algebraische Gleichungen, bei denen man sich nur für die ganzzahligen Lösungen
interessiert [FuRo].
Die Holztafeln sind in der Sprache Kanbun, einer alten Form des Japanischen,
geschrieben. Kanbun hat eine ähnliche Bedeutung wie Latein bei uns:
Wissenschaftliche Werke der Edo-Zeit sind hauptsächlich in dieser Sprache verfasst.
Es gibt jedoch nur wenige Japaner, die Kanbun noch fließend lesen können. Vielen
Wissenschaftlern, die sich mit Sangakus beschäftigen wollen, bereitet die
Entschlüsselung dieser Sprache Schwierigkeiten [FuRo].
Die älteste noch erhaltene Sangaku-Tafel stammt aus dem Jahre 1683 und die erste
Sammlung von typischen Sangaku- Aufgaben wurde 1789 in Buchform
veröffentlicht. Zur heutigen Zeit sind noch mehr als 880 Holztafeln erhalten, wobei
noch weitere hundert in Sammlungen zitiert werden [FuPe]. Das Auffinden von
Sangaku-Tafeln war relativ gleichmäßig über Japan verteilt, es ließ sich also kein
besonders häufiges Auftreten in ländlichen oder in städtischen Regionen feststellen.
Die folgenden Abbildungen zeigen eine Landkarte von Japan mit japanischen
Städten und eine andere mit der Anzahl der in den Regierungsbezirken gefundenen
Sangaku-Tafeln:
6
Vgl. [D].
Vgl. [FuPe]. Anzahl der in jedem Regierungsbezirk gefundenen
Sangaku-Tafeln
7
3 Geschichtlicher Hintergrund
3.1 Allgemeiner Überblick über die Geschichte der japanischen
Mathematik
Ich orientiere mich in diesem Teil meiner Arbeit größtenteils am Buch „5000 Jahre
Geometrie“, das im Literaturverzeichnis unter [ScSc] zu finden ist.
Um historische Fakten über die japanische Mathematik erfahren zu können, muss
man sich hauptsächlich an einer Darstellung von Mikami aus dem Jahre 1913
orientieren bzw. einer Ausarbeitung von Mikami und Smith aus dem folgenden Jahr,
da ansonsten keine Informationen in westlicher Sprache bekannt sind.
Diese Autoren teilen die mathematische Entwicklung Japans in sechs Epochen ein:
Bis 552
Vor dieser Zeit war Japan nur wenig und indirekt von der chinesischen
Mathematik beeinflusst, sonst weitgehend unabhängig.
552-1603
In dieser Periode lässt sich eine starke Beeinflussung durch die
chinesische Wissenschaft feststellen; sie wird später auch als das
japanische Mittelalter bezeichnet.
1603-1675
Diese Zeit wird auch als die Renaissance der japanischen Mathematik
bezeichnet. Auch in diesem Zeitraum ist ein Eindringen der
chinesischen Wissenschaft festzustellen, aber auch erste Strömungen
der europäischen Wissenschaft werden wahrgenommen. Diese Zeit
gehört schon zur japanischen Edo-Periode, in der die Sangakus
entstanden sind.
1675-1775
In dieser Periode ist Japan fast vollständig von der westlichen Welt
abgeschottet und zwei wichtige Mathematiker Japans, Seki Kowa und
sein Schüler Takebe, bereiten in ihren Arbeiten die Entwicklung der
einheimischen Wasan-Mathematik vor.
8
1775-1868
Während dieser Zeit entstehen die meisten Sangakus und man
bezeichnet diesen Zeitraum als Höhepunkt der eigenständigen
japanischen Mathematik.
Ab 1868
Von dieser Zeit an erfolgt wieder eine schrittweise Öffnung zur
westlichen
Welt
und
damit
eine
immer
stärker
werdende
Beeinflussung durch die westliche Mathematik.
In einem späteren Werk über die Geschichte der japanischen Wissenschaft, dem
Buch „Science and Culture in Traditional Japan“ von M. Sugimoto und D. L. Swain,
das 1978 erschienen ist, erhält man eine aufschlussreiche Beschreibung der
kulturellen und sozialen Hintergründe der japanischen Wasan-Mathematik.
3.2 Die Renaissance der japanischen Mathematik
Die Zeit der Renaissance der japanischen Mathematik beginnt, als es zunächst noch
engere Kontakte zur europäischen Welt gibt. Nach einem Machtwechsel in der
Regierung Japans werden neue Handelsbeziehungen zur westlichen Welt aufgebaut
und die Jesuiten beginnen das Land zu missionieren. Es ist festzustellen, dass in
dieser Epoche die Entwicklung der japanischen Mathematik merklich von der
europäischen Wissenschaft geprägt war. Nachdem aber in der ersten Hälfte des 17.
Jahrhunderts (wahrscheinlich bis 1639) bereits wieder eine Gegenbewegung zur
politischen Entwicklung der letzten Jahrzehnte einsetzt, isoliert sich Japan völlig von
der westlichen Welt. Diese Isolation, die von den damaligen Machthabern zur
Festigung ihrer Führungsrolle verhängt wurde, wird bis ungefähr 1860 dauern, bis
US-amerikanische Kriegsschiffe die Isolation gewaltsam beenden.
Der totale Ausschluss der westlichen Welt hat jedoch nicht nur negative Folgen.
Kunst und Kultur entwickeln sich im späten 17. Jahrhundert so ausgezeichnet, dass
diese Jahre mit dem Namen „genroku“, was so viel wie Renaissance bedeutet,
bezeichnet werden. Eben in dieser Zeit beginnt in Japan auch eine neue
Mathematikkultur zu wachsen, die durch die einmalige Entwicklung des Wasan
9
gekennzeichnet ist. Wasan bedeutet übersetzt „Japanische Mathematik“. In dieser
Mathematik, die zunächst hauptsächlich von gebildeten Bürgern der Samurai-Klasse
betrieben
wird,
lassen
sich
kaum
mathematische
Begriffsbildungen
und
philosophische Reflexionen finden und es ist im Wesentlichen kein Praxisbezug zu
alltäglichen Problemen oder Fragen festzustellen. Die Beschäftigung mit Sangakus
ist vielmehr als ein intellektueller Zeitvertreib zu verstehen, was man in der heutigen
Zeit vielleicht mit dem Lösen von Sudokus (japanisches Zahlenrätsel) vergleichen
kann. Man muss aber auch anmerken, dass diese mathematische Renaissance unter
der Beeinflussung durch die chinesischen Mathematik stand, welche sogar in
einzelnen Texten als die Quelle der japanischen Mathematik bezeichnet wird.
Außerdem
werden in
dieser
Zeit
der
Isolation
verstärkt
mathematische
Rechenoperationen gelehrt, wie zum Beispiel das elementare Rechnen auf dem
Rechenbrett, aber auch das Wurzelziehen mit Hilfe von Rechenstäben. Weiter wird
Wert gelegt auf die Berechnungen von Flächen- und Rauminhalten. Für die
Ermittlung der Kreisfläche lassen sich zu dieser Zeit in Japan für die Kreiszahl
die Näherungen 3,16 und
10

finden. Diese im Alltag anwendbaren
mathematischen Gesetzmäßigkeiten ergänzen in der Zeit der Renaissance die
praxisferne Wasan- Mathematik und sind vor allem bei der Arbeit von Kaufleuten
und Handwerkern von großem Nutzen.
3.3 Takakazu Seki Kowa
Diese Abbildung ist zu finden unter der Quelle [A1].
10
Der wichtigste Mathematiker dieser Zeit in Japan war Takakazu Seki Kowa. Seki
wurde im März 1642 in Fujioka in Japan geboren und wuchs in einer adligen Familie
auf, die ihn kurz nach seiner Geburt adoptiert hatte. Er wurde von einem Hauslehrer
unterrichtet, der schon früh Sekis außergewöhnliches mathematisches Talent
erkannte. Wenige Jahre später baute er eine Bibliothek auf, in der er japanische und
chinesische Werke über Mathematik sammelte. So wurde er bald als ein Experte im
Bereich der Mathematik anerkannt. Er wurde als „The Arithmetical Sage“
bezeichnet, was soviel heißt wie „Der Weise im Bereich der Arithmetik“ und wurde
ein erfolgreicher Lehrer der von ihm gegründeten Seki-Schule. In vielen seiner
Werke griff er Entdeckungen der westlichen Mathematik vor. Seki leistete einen
wichtigen Beitrag bei der Entdeckung der Determinanten (1683). Zwar behandelte er
nur 2x2- und 3x3-Matrizen und schaffte es nicht, die Berechnung auf den
allgemeinen Fall zu erweitern, war aber trotzdem allgemeiner als Leibniz, der zehn
Jahre später, unabhängig von Seki, Determinanten zur Lösung von Gleichungen
benutzte.
Ein weiterer bedeutender Erfolg Sekis war die Entdeckung der Bernoulli-Zahlen vor
Bernoulli
selbst.
Außerdem
benutzte
er
bereits
1685
ein
Schema
zur
Nullstellenberechung, das erst 100 Jahre später von Horner bekannt gemacht wurde.
Eine dritte Leistung, die Seki zugeschrieben wird, und die für die japanische
Tempelgeometrie äußerst relevant ist, ist das Kreisprinzip, damals „enri“ genannt. Es
hat große Ähnlichkeit mit der Exhaustionsmethode, welche von den griechischen
Mathematikern Eudoxos und Archimedes zur Berechnung der Kreisfläche entwickelt
wurde. Seki zerlegte einen Kreis in n Rechtecke, während die griechischen
Mathematiker den Kreis durch n-seitige Polygone annäherten.
Seki Kowa starb schließlich vor 300 Jahren am 24. Oktober 1708 in Edo, dem
heutigen Tokio.
Vgl. für diesen Abschnitt die Quellen [A1] und [A2].
11
4 Die Geometrie in der Wasan- Mathematik
4.1 Allgemeines
Als Grundlage für die Wasan–Mathematik erlangt vor allem ein mathematisches
Werk besondere Bedeutung. Dies ist das wohl bekannteste Lehrbuch aus der Zeit der
Ming-Dynastie, das 1627 von Yoshida Shichibei Koyu verfasst wurde. Der Titel
dieses Buches „Jinko-ki“ bedeutet sinngemäß soviel wie „Abhandlung über Zahlen
von der größten bis zur kleinsten“ [ScSc] und dieses Lehrbuch wird nach Yoshidas
Tod von vielen Autoren gern als Vorbild genommen. Wie auch beim Kreieren von
Sangaku-Tafeln, werden in diesem Werk ungelöste Aufgaben als Herausforderung
an andere Mathematiker in die eigenen Aufgabensammlungen mit aufgenommen
oder von anderen gestellte Aufgaben gelöst. Diese Art der mathematischen
Diskussion wurde auch in Europa von dem französischen Mathematiker Pierre de
Fermat betrieben. Er hatte es sich im 17. Jahrhundert zur Aufgabe gemacht, durch
regelmäßige Briefwechsel mit anderen Wissenschaftlern gemeinsam mathematische
Probleme und Fragen zu erörtern und neue Ideen zu diskutieren [L]. Auf diesem
Weg wurde also früher in vielen Teilen der Welt mathematisches Wissen verbreitet
und Grundlagen für die Entwicklung dieser Wissenschaft gelegt.
Ein Thema, das in der japanischen Mathematik dieser Zeit sehr beliebt war, ist das
Problem der systematischen Berechnung von regelmäßigen Vielecken. Dieses
Problem wurde sehr unterschiedlich und teilweise äußerst raffiniert bearbeitet und es
wurden viele ähnliche Aufgabenstellungen dazu gefunden. So gibt es zum Beispiel
eine Aufgabe, bei der in einen gegebenen Kreis 19 kleinere Kreise ringförmig so
einzupassen sind, dass diese je ihre beiden Nachbarn und den gegebenen Kreis
berühren und unter den gleichen Bedingungen 19 Kreise außen tangential als Ring
angelegt werden. Gesucht sind schließlich die Radien der einbeschriebenen und
umbeschriebenen Kreise. In diesem Problem ist die Frage nach einem regelmäßigen
Neunzehneck versteckt [ScSc].
Ingesamt ist festzustellen, dass es beliebt war, Aufgaben zu stellen, die in
Alltagsprobleme eingekleidet sind und den Anschein von Relevanz für die Praxis
erfüllen.
12
Viel Beachtung wurde in der japanischen Mathematik dieser Zeit auch dem so
genannten Enri- oder Kreisprinzip geschenkt. Dies beinhaltet ein Verfahren zur
Bestimmung der Länge eines Kreisbogens bzw. dem Umfang eines Kreises und
damit eine Möglichkeit, die Kreiszahl π relativ genau zu berechnen. Ein japanischer
Mathematiker, der sich um diese Problemlösung verdient gemacht hat, ist Takebe,
der von Seki Kowa unterrichtet wurde. Sein Verfahren ähnelt der heutigen
Infinitesimalrechnung, wobei von seinem Schüler Takebe über einen geometrischen
Ansatzpunkt eine Reihenentwicklung für die Berechnung eines Kreisbogens
gefunden wurde. Diese Methode ist eng verwandt mit der Exhaustionsmethode,
welche die griechischen Mathematiker Eudoxos und Archimedes zur Berechnung der
Kreisfläche entwickelten. Während diese den Kreis durch n-seitige Polygone
approximieren, wird er im enri in n Rechtecke zerlegt; entsprechend unterscheiden
sich die Grenzprozesse voneinander [FuRo].
Allgemein muss man feststellen, dass die japanische Tempelgeometrie eher als eine
Art Aufgabensammlung zu verstehen ist, die von den verschiedensten mathematisch
interessierten Japanern geschaffen wurde. Es gibt keine neuen Lehrsätze, die für die
Entwicklung der weltweiten Geometrie von Bedeutung wären und auch sonst kaum
mathematische Entdeckungen, die für die Nachwelt festgehalten wurden. Zwar steht
fest, dass Seki wichtige Entdeckungen schon vor den heute bekannten Erfindern
einiger mathematischer Sätze gemacht hat (Bernoulli und Descartes), jedoch wurden
seine Erfindungen nicht ausreichend bekannt gemacht, was wohl an der Isolation
Japans zu seiner Zeit lag.
Die Tatsache, dass aus der japanischen Wasan–Mathematik kaum neue Lehrsätze
hervorgingen, führt auch dazu, dass über diese Mathematik sehr wenig bekannt ist
und dass sie im Laufe der Zeit immer mehr in Vergessenheit geriet und sich dies in
Zukunft wahrscheinlich noch fortsetzen wird.
13
4.2 Interessante Entdeckungen
Im Folgenden möchte ich nun einige interessante Probleme darstellen, die bereits in
Japan in der Edo-Mathematik entdeckt wurden, jeweils einige Zeit vor den
bekannten Entdeckern in Europa. Dies ist jedoch kaum bekannt, weshalb die
japanischen Mathematiker heute selten damit in Verbindung gebracht werden.
4.2.1 Das Malfatti-Problem
Folgende Skizze stellt das Malfatti-Problem dar:
A
O1
O2
B
O3
C
Die drei Kreise k1(O1;r1), k2(O2;r2) und k3(O3;r3) berühren sich gegenseitig jeweils
von außen her. Das Dreieck ABC wird gebildet von den drei Tangenten an die
Kreise.
Gesucht sind nun die Radien der drei Kreise r1, r2 und r3 in Abhängigkeit von den
Dreiecksseiten a, b und c und anschließend der Radius des Inkreises des Dreiecks
ABC.
Dieses Problem wurde offiziell im Jahre 1803 von Gian Francesco Malfatti gestellt
und im gleichen Jahr von diesem auch gelöst.
Interessant ist aber zu erfahren, dass der japanische Mathematiker Chokuen Ajima,
der von 1732 bis 1798 lebte, bereits dieses Problem gestellt hatte und im Zeitraum
von 1771-1773, also mindestens 30 Jahre vor Malfatti selbst, eine Lösung dazu fand.
14
Außer einer allgemeinen Lösung veröffentlicht Ajima zusätzlich eine Lösung mit
Zahlenbeispielen, da man in dieser Zeit bemüht war, stets rationale Lösungen zu
Problemen aller Art anzugeben.
Im Folgenden möchte ich nun eine Lösung des Malfatti-Problems darstellen. Hierzu
benötige ich zunächst einige Hilfslinien und neue Bezeichnungen:
C
d3
90 ° H
I
90 °
r3
90 °
G
90 °
K
r2
r1
90 °
A
d1
E
90 °
d2
F
B
Um die Strecke EF zu bestimmen, wende ich zunächst den Satz des Pythagoras an
und bekomme damit: (r1+r2)² = (r2-r1)² + EF²
Durch Umformen: EF² = r1² + 2r1r2 + r2² - r2² + 2r1r2 – r1²
Und schließlich: EF = 2 r1 r2 .
Analog gehe ich für die Strecken GH und IK vor, so dass ich folgende Gleichungen
erhalte: GH = 2 r2 r3 und IK = 2 r3 r1 .
Hieraus ergeben sich folgende drei Gleichungen für die Dreiecksseiten a, b und c:
c = d1 + 2 r1 r2 + d2
(1)
a = d2 + 2 r2 r3 + d3
(2)
b = d3 + 2 r3 r1 + d1
(3)
Da die drei Kreise jeweils auf den drei Winkelhalbierenden des Dreiecks liegen,
gelten auch folgende Beziehungen:
r
1
tan(  ) = 1
2
d1
15
r
1
tan(  ) = 2
2
d2
r
1
tan(  ) = 3
2
d3
wobei  der Winkel bei A,  der Winkel bei B und  der Winkel bei C ist.
Anschließend quadriere ich die Gleichungen 1, 2 und 3 und stelle sie wie folgt um:
4r1r2 = (d1 + d2 – c)²
4r2r3 = (d2 + d3 – a)²
4r1r3 = (d1 + d3 – b)²
Mit Hilfe des Halbwinkelsatzes erhält man außerdem:
r
1
tan(  ) = 1 =
2
d1
(
a  b  c 2b a  b  c 2c
 )(
 )
2
2
2
2
a  b  c a  b  c 2a
(
)(
 )
2
2
2
Durch Quadrieren und anschließendem Umformen erhält man folgende Gleichung:
2bc(d1² - r1²) = (d1² + r1²) (-a² + b² + c²)
Analog geht man für die drei anderen Winkel vor und bekommt schließlich weitere
zwei Gleichungen:
2ac(d2² - r2²) = (d2² + r2²) (a² – b² + c²)
2ab(d3³ - r3²) = (d3² + r3²) (a² + b² - c²)
Um nun auf die Lösung zu kommen, muss der Schnitt von zwei Kegelschnitten
berechnet werden.
Für den Radius r des größten Kreises gilt dann in Abhängigkeit der Radien r1, r2, r3:
r=
r1 r2 r3 ( r1  r2  r3  r1  r2  r3 )
r1 r2  r2 r3  r3 r1
=
2 r1 r2 r3
r1  r2  r3  r1  r2  r3
.
Vgl. für die ausführliche Lösung [FuPe], [Ste], [F] und [G].
16
4.2.2 Das Casey-Theorem
Folgende Skizze zeigt das Casey-Theorem:
r1
r2
O1
O2
r5
O5
O3
r3
O4
r4
Das Casey-Theorem ist ein Theorem aus der euklidischen Geometrie, das nach dem
englischen Mathematiker John Casey benannt ist. Er hat es 1857 aufgestellt und es
besagt Folgendes:
Vier Kreise k1, k2, k3, k4 sind Tangenten an einen gegebenen Kreis oder eine gerade
Linie, genau dann, wenn gilt: T12T34  T14T42  T14T23 = 0, wobei Tij die Länge
einer gemeinsamen Tangente von dem Kreis ki und kj ist.
Die Notwendigkeit, dass diese Beziehung gilt, wurde bereits 1830 von dem
japanischen Mathematiker Chochu Siraisi festgestellt, also fast 30 Jahre, bevor Casey
dies bekannt gemacht hat.
Für die folgende Lösung vergleiche die Quellen [FuPe] und [H].
Zunächst wird für die Skizze ein Koordinatensystem festgelegt, wobei das Quadrat
die Seitenlänge 1 hat. Die linke untere Ecke des Quadrats liegt im Ursprung (0,0)
und die rechte obere Ecke hat die Koordinaten (1,1).
17
Für den mittleren Kreis mit dem Mittelpunkt O5 werden die Koordinaten (x,y)
festgelegt. Für die anderen Kreismittelpunkte gilt mit diesen Voraussetzungen und
den bereits bekannten Radien:
O1 (1 - r1, 1 – r1)
O2 (r2, 1 – r2)
O3 (r3, r3)
O4 (1 – r4, r4)
Mit Hilfe des Satzes des Pythagoras ergeben sich folgende Gleichungen:
(1 – r4 – c)² + (y – r4)² = (r + r4)²
(1 – r1 – x)² + (1 – r1 – y)² = (r + r1)²
(x – r3)² + (y – r3)² = (r + r3)²
(x – r2)² + (1 – r2 – y)² = (r + r2)²
Für die weiteren Schritte werden in der Skizze weitere Bezeichnungen eingeführt:
T12
r1
r2
O1
O2
c 13
T23
r5
90 °
T14
O5
T13
90 °
O3
r3
90 °
O4
r4
T34
Hierbei beschreiben die Tangenten Tij jeweils die Entfernungen zwischen den zwei
Berührpunkten an den Kreisen ki und kj.
Für die Tangentenabschnitte Tij gilt also offensichtlich, wobei die Seitenlänge des
Quadrats 1 ist:
18
T12 = 1 – r1 – r2
T34 = 1 – r3 – r4
T14 = 1 – r1 – r4
T23 = 1 – r2 – r3
Werden mit cij die Entfernungen von einem Mittelpunkt Oi zum Mittelpunkt Oj
bezeichnet, ergibt sich mit Hilfe von Pythagoras für die weiteren Tangenten:
c13² = (1 – r1 – r3)² + (1 – r1 – r3)² = 2(1 – r1 – r3)²
c24² = (1 – r2 – r4)² + (1 – r2 – r4)² = 2(1 – r2 –r4)²
Außerdem findet man auch folgende Zusammenhänge:
c13² = T13² + (r3 – r1)²
Umgeformt nach T13 ergibt dies:
T13² = c13² - (r3 – r1)²
Schließlich radiziere ich noch:
T13 =
c13  (r3  r1 )² =
2
2(1  r1  r3 )²  (r3  r1 )²
Analog gehe ich für die Tangente T24 vor:
c24² = T24² + (r2 – r4)²
bzw. T24 =
c24  (r2  r4 )² =
2
2(1  r2  r4 )²  (r2  r4 )²
Da alle vier Kreise Tangenten an den Kreis 5 sind, ergibt sich:
T12  T34  T14  T23  T13  T24 =
= (1 – r1 – r2)(1 – r3 – r4) + (1 – r1 – r4)(1 – r2 – r3) -
[2(1  r1  r3 )²  (r3  r1 )²][2(1  r2  r4 )²  (r2  r4 )²]  0
Hiermit ist die Behauptung gezeigt.
19
Diese Beispiele zeigen eindrucksvoll, dass in der japanischen Wasan-Mathematik
sehr wohl interessante Erkenntnisse und Ergebnisse gewonnen wurden. Diese
wurden jedoch wegen der Isolation Japans meist nicht verbreitet und blieben für die
westliche Welt größtenteils unbekannt, weshalb auch kaum japanische Mathematiker
dieser Zeit zu heute bekannten Wissenschaftlern gezählt werden.
20
5 Wichtige Sätze, die häufig zur Lösung von SangakuProblemen benötigt werden
Im Folgenden werde ich einige mathematische Sätze vorstellen, die man heute häufig
zur Lösung von Sangaku-Aufgaben verwenden kann, bzw. die mir bei der Lösung
von Aufgaben hilfreich waren.
5.1 Der Satz des Pythagoras
Ein bedeutender Satz, der in vielen Sangaku-Lösungen gebraucht wird, ist der Satz
des Pythagoras, zusammen mit seinem Höhensatz und den Kathetensätzen.
Diese Sätze lauten folgendermaßen:
C
90 °
b
a
h
90 °
q
p
A
c
B
In einem rechtwinkligen Dreieck ABC gilt, wenn die Bezeichnungen wie in obiger
Skizze sind:
(1) a² + b² = c² (Satz des Pythagoras)
(2) c  p = b² (1. Kathetensatz)
(3) c  q = a² (2. Kathetensatz)
(4) p  q = h² (Höhensatz)
Vgl. [BMNW].
21
In Sangakus kommen häufig Dreiecke vor, z.B. Dreiecke, in die Kreise
einbeschrieben sind oder Dreiecke, die in Kreiskonstruktionen auftauchen und die
man dann so in rechtwinklige Dreiecke umformen muss, dass man die Seiten mit
Hilfe gegebener Radien oder anderen Strecken über die Satzgruppe des Pythagoras
berechnen kann. Zudem ist es meist notwendig, dass man geeignete Hilfslinien bzw.
ganze Hilfsdreiecke einzeichnet, damit überhaupt bestehende Zusammenhänge klar
werden und Berechnungen über bekannte Methoden ermöglicht werden. In einem
späteren Teil meiner Arbeit werde ich einige Sangaku-Lösungen vorstellen, bei
denen die Notwendigkeit von Hilfsdreiecken deutlich wird, damit die Seitenlängen
durch bekannte Größen ausgedrückt werden können. Meist reicht aber eine einfache
Anwendung eines Satzes der Pythagorassatzgruppe nicht aus, sondern es müssen
geschickt mehrere Beziehungen aufgestellt werden, so dass durch gegenseitiges
Einsetzen und sinnvolles Gleichsetzen die gesuchten Beziehungen erreicht werden
können.
5.2 Sätze über Tangenten und Sekanten
Weitere wichtige mathematische Aussagen, die man oft benutzen muss, sind Sätze
über Tangenten am Kreis. Hierzu gehört als erstes, dass Tangenten an einen Kreis
stets senkrecht auf den Kreisradius stehen.
Außerdem benötigt man den Satz vom gemeinsamen Tangentenabschnitt. Dieser
besagt, dass es zu einem Punkt P außerhalb des Kreises K stets zwei Tangenten T
und T` durch P gibt, wobei C und C` die Berührpunkte der Tangenten an den Kreis
sind. Die Tangentenabschnitte PC und PC` sind dann gleichlang, es gilt also:
PC =PC`. Vgl. [B].
C
P
r
k
M
C`
22
Zusätzlich benötigt man häufig den so genannten Sekanten-Tangentensatz. Dieser
besagt Folgendes:
PA  PA` PB  PB` PT 2 .
Hier sind A, A`, B und B` Schnittpunkte zweier
T
90 °
A`
A
Sekanten durch einen Punkt P außerhalb des
Kreises mit der Kreislinie und T ist der
P
M
Berührpunkt der Tangente durch den Punkt P.
B
Vgl. [BMNW].
B`
B
Wichtig ist auch der Sehnensatz:
Er sagt etwas über die Verhältnisse zweier
D
sich schneidender Sehnen in einem Kreis:
SA  SB  SC  SD . (vgl. Skizze)
S
C
Vgl. [BMNW].
M
A
5.3 Ähnlichkeitssätze
Neben diesen Aussagen über Verhältnisse zwischen Geraden und Kreisen benötigt
man auch die Ähnlichkeitssätze in Dreiecken.
In der Geometrie sind zwei Figuren zueinander ähnlich, wenn sie durch eine
Ähnlichkeitsabbildung, also eine geometrische Abbildung, die sich aus einer
zentrischen Streckung und einer Kongruenzabbildung zusammen setzen lässt,
ineinander überführt werden können. In ähnlichen Figuren stimmen Winkel und
Streckenverhältnisse überein.
Im Einzelnen gibt es vier Ähnlichkeitssätze über Dreiecke:

Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln
übereinstimmen.

Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen
entsprechender Seiten übereinstimmen.

Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im
Verhältnis der anliegenden Seiten übereinstimmen.
23

Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten
und im Gegenwinkel der größeren Seite übereinstimmen.
Vgl. [O].
24
6 Einige Sangaku-Aufgaben
In diesem Teil meiner Arbeit werde ich nun einige Sangaku-Aufgaben vorstellen und
meine Lösungsvorschläge dazu ausführen. Zum letzten Sangaku werde ich außerdem
eine Original-Lösung präsentieren.
6.1 Sangaku 1
Dieses Problem ist auf einer Holztafel von 1824 zu finden [FuPe].
Gegeben sind drei Kreise, wobei alle eine gemeinsame Linie als Tangente haben und
der Kreis k3 vom Radius r3 um den Mittelpunkt M3 die beiden größeren Kreise k1,
mit dem Radius r1 und dem Mittelpunkt M1 und k2 mit dem Radius r2 und dem
Mittelpunkt M2 wie in folgender Zeichnung berührt:
M1
M2 r2
r1
M3
r3
Es ist nun zu zeigen, dass gilt:
1
1
1
.


r3
r1
r2
Um dies beweisen zu können, zeichne ich einige geeignete Hilfslinien in die Skizze
ein:
25
M1
y
M2 r2
r1
r1+r2
r1-r3
r1+r3
x
I: Nach dem Satz des Pythagoras gilt:
M3
r3
r2+r3
(r1-r3)² + x² = (r1+r3)²
Durch Ausmultiplizieren erhalte ich:
r1² - 2r1r3 + r3² + x² = r1² + 2r1r3 + r3²
Nach Kürzen bleibt übrig:
x² = 4r1r3
Durch Radizieren ergibt sich:
x = 2 r1r3
II: Auch hier gilt nach Pythagoras:
(r1-r2)² + y² = (r1+r2)²
Nach Ausmultiplizieren gilt:
r1² - 2r1r2 + r2² + y² = r1² + 2r1r2 + r2²
Nach Kürzen gilt dann:
y² = 4r1r2
Durch Radizieren ergibt sich:
y = 2 r1r2
III: Wie in I und II gilt:
(y-x)² + (r2-r3)² = (r2+r3)²
Durch Ersetzen von y und x durch die Ausdrücke aus I und II, Ausmultiplizieren
und anschließendem Kürzen erhält man:
(2 r1r2 - 2 r1r3 )² + r2² - 2r2r3 + r3² = r2² + 2r2r3 + r3²
4r1r2 – 8r1 r2 r3 + 4r1r3 = 4r2r3
Diesen Ausdruck teile ich zunächst durch 4 und faktorisiere ihn dann mit Hilfe
der binomischen Formel:
r1r2 – 2r1 r2 r3 + r1r3 = r2r3
26
( r1r2 -
r1r3 )² = r2r3
Nun radiziere ich den Ausdruck und bekomme somit Folgendes:
r1r2 -
r1r3 =
r2 r3
Anschließend addiere ich den Term
r1r2 =
r2 r3 +
r1r3 und dividiere dann durch r1 r2 r3 :
r1r3
1
1
1
=
.

r3
r1
r2
Dies ist das gewünschte Ergebnis.
Bei dieser Sangaku-Aufgabe ist es wichtig, dass man sich gleich zu Beginn geeignete
Hilfslinien einzeichnet, um rechtwinklige Dreiecke zu erhalten, bei denen man den
Satz des Pythagoras anwenden kann. Hat man diese Hilfsdreiecke eingezeichnet und
die Zusammenhänge zwischen den drei Radien erkannt, dann sind fast nur noch
elementare algebraische Umformungen durchzuführen, um das Ergebnis zu erhalten.
Kommt man nicht sofort auf die Idee, wie man geeignet dividieren und kürzen muss,
so ist es zunächst auch möglich, vom Ergebnis her rückwärts zu rechnen und sich
von zwei Seiten einander anzunähern und so auf das gewünschte Resultat zu
kommen.
6.2 Sangaku 2
Dieses Problem ist auf einer Sangaku- Tafel aufgemalt, auf der gegen die
Gewohnheit kein Datum festgehalten wurde. Es ist jedoch bekannt, dass es im
japanischen Regierungsbezirk Hyogo gefunden wurde [FuPe].
A
E
90 °
B
D
C
27
Problem:
Das Dreieck ABC hat bei C einen rechten Winkel. AD ist die Winkelhalbierende des
Winkels ACD. Die Strecke ED ist parallel zu der Seite AC, wobei der Punkt D auf
der Seite BC liegt und der Punkt E auf AB.
Es soll nun gezeigt werden, dass gilt:
1
1
1


.
ED AC AB
Beweis:
Da ED nach Voraussetzung parallel zu AC ist, muss bei D auch ein rechter Winkel
sein, d.h. EDB = 90°.
Nach dem Satz über Stufenwinkel gilt außerdem: BED = BAC .
Nach Voraussetzung ist AD Winkelhalbierende, woraus sich ergibt:
BAD = DAC =
1
1
 BAC =  BED .
2
2
Wir betrachten nun das Dreieck ADC. Dort gilt für den Winkel ADC :
ADC = 180° - 90° - DAC = 90° - DAC = 90° - BAD .
Weiter gilt nun, da nach dem Nebenwinkelsatz auch CDE ein rechter Winkel ist:
ADE = 90° - ADC = 90°- (90° - BAD ) = BAD .
Da also die Winkel ADE und BAD im Dreieck AED gleichgroß sind, ist das
Dreieck AED gleichschenklig und die Seiten AE und ED sind gleichlang.
Es gilt offensichtlich: BE = AB – AE und mit obiger Feststellung also:
BE = AB – AE = AB – ED.
Außerdem gilt nach dem Strahlensatz:
ED BE

.
AC AB
In diesem Ausdruck ersetze ich nun BE durch obige Beziehung BE = AB – ED und
bekomme:
ED AB  ED
ED

=1.
AC
AB
AB
Ich addiere nun
ED
ED
ED
, so dass 1 alleine auf einer Seite steht:
+
= 1.
AB
AC
AB
Anschließend muss ich nur noch durch ED dividieren:
1
1
1
+
=
.
AC
AB ED
Dies ist genau die Beziehung, die gezeigt werden sollte.
28
6.3 Sangaku 3
Dieses Sangaku ist auf einer noch existierenden Holztafel von 1895 zu finden, die
im Regierungsbezirk Fukusima aufgehängt war. [FuPe]
In diesem Sangaku sind die Radien des kleinen Kreises (ganz oben) und des etwas
größeren Kreises (über dem kleinen Quadrat) zu bestimmen.
Um den Beweis führen zu können, zeichne ich einige Hilfslinien ein und benenne
benötigte Strecken und Punkte:
D
L
H
C
M
N
G
a
b
A
E
K
F
B
29
Lösung:
Der Kreis mit dem Radius a um den Mittelpunkt B berührt den kleinen Kreis an
einem Punkt O. Auf der Verlängerung der Strecke BO liegt der Mittelpunkt des
kleinen Kreises M, wobei für die Länge der Strecke BM gilt: BM= a + r.
Die Strecke KM ist parallel zu den Seiten AD und BC und hat offensichtlich die
Länge
KM= a - r.
Zur Bestimmung von r betrachten wir nun das rechtwinklige Dreieck BMK mit
seinem rechten Winkel bei K und der Seite KB =
a
. Nach Pythagoras gilt hier mit
2
den vorhergehenden Überlegungen:
2
a
(a – r)² +   = (a + r)²
2
Diesen Term forme ich um:
a² – 2ar + r² +

a²
= a² + 2ar + r²
4
a²
= 4ar
4
r=
a
.
16
Zur Bestimmung des Radius R des großen Kreises benötigen wir zunächst die
Seitenlänge b des kleinen inneren Quadrates EFGH:
Hierfür betrachte ich das rechtwinklige Dreieck BHE. Da der Punkt H auf dem Kreis
um den Mittelpunkt B mit dem Radius a liegt, gilt für die Länge der Seite BH:
BH = a.
Außerdem ist EH eine Seite des kleinen Quadrats und entspricht somit der gesuchten
Seitenlänge b.
Die Strecken AE und FB sind gleichlang, da das kleine Quadrat offensichtlich zentral
auf der Seite AB liegt und es gilt: AE  FB 
a b
.
2
Also gilt für die Seite EB des rechtwinkligen Dreiecks BHE: EB= b +
a b
.
2
30
Mit Pythagoras ergibt sich also:
b² + (b +
a b
)² = a²
2
Dies forme ich wieder um:
b² + (
ba
)² = a²
2
 b² +
a ²  2ab  b ²
= a²
4
 4b² + a² + 2ab + b² = a²
 5b² + 2ab – a² = 0
Diese quadratische Gleichung löse ich mit Hilfe der Lösungsformel für quadratische
Gleichungen nach b auf und erhalte für b zunächst die zwei Lösungen b1 = -a und
b2 =
3
a.
5
Da aber eine Seitenlänge nicht negativ und auch nicht 0 sein kann, muss b2 die
gesuchte Lösung sein. Wir rechnen also im Folgenden mit b =
3
a.
5
Um nun den Radius R des großen Kreises bestimmen zu können, betrachte ich nun
das rechtwinklige Dreieck BNK. Hier gilt aus ähnlichen Gründen wie oben im
Dreieck BMK für die drei Dreiecksseiten:
KB =
a
, BN = a – R und KN = b + R.
2
Nach Pythagoras gilt also wieder:
2
a
  + (b + R)² = (a – R)²
2

a²
+ b² + 2bR + R² = a² - 2aR + R²
4

16
39
aR =
a²
5
100
R=
39
a.
320
Hiermit sind die Radien beider Kreise bestimmt.
31
6.4 Sangaku 4
Dieses Sangaku stammt von 1814 und wurde in dem Regierungsbezirk Chiba
gefunden.
Dieses Problem wird als „Keksproblem 108“ an der Uni Würzburg behandelt und ist
zu finden unter: http://www.mathematik.uni-wuerzburg.de/~keks/kekse.html.
A
Problemstellung:
O1
I
O3
O2
B
C
Der Kreis mit dem Mittelpunkt I und dem Radius r ist Inkreis des Dreiecks ABC. Die
Kreise k1(O1;r1), k2(O2;r2) und k3(O3;r3) berühren die Dreiecksseiten AB und AC, BA
und BC, CA und CB. Zusätzlich berühren alle drei kleinen Kreise den großen Kreis
an seiner Außenseite.
Nun soll gezeigt werden, dass gilt: r 
r1 r2 
r2 r3 
r3 r1 .
Die folgende Lösung ist nun eine Originallösung, die in einem Buch von 1810
erschienen ist. Einige Rechenschritte, die für die Lesbarkeit des Beweises
erforderlich sind, wurden von mir beigefügt.
32
Zunächst werden in der Originallösung folgende Hilfsbezeichnungen eingeführt:
A
C1
B3
O1
C2
B2
I
C3
O3
O2
B
A1
B1
A3
A2
C
Um nun auf den ersten Schritt aus der japanischen Lösung zu kommen, benötige ich
zunächst noch einige Hilfslinien:
C2
A
C1
r1 B3
O1
B2
I
C3
O2
B
r
r-r3
r2
A1
r3
90 °
A2
A2A3
O3
B1
A3
C
Da es sich bei meinem eingezeichneten Hilfsdreieck um ein rechtwinkliges Dreieck
handelt, gilt nach Pythagoras:
(A2A3)² + (r – r3)² = (r3 + r)²
Durch Ausmultiplizieren um Umstellen erhalte ich folgendes:
(A2A3)² = r3² + 2rr3 + r² - r² + 2rr3 – r3²
Nun kürze ich noch:
(A2A3)² = 4rr3
Und schließlich radiziere ich noch:
A2A3 = 2 rr3
33
Analog gehe ich für die Strecken C2C3 und B2B3 vor, so dass man schließlich folgern
kann, wie es in der Originallösung zu finden ist:
Es bestehen also folgende Gleichheiten:
A2A3 = 2 rr3 , C2C3 = 2 rr2 , B2B3 = 2 rr1
Deshalb gilt auch:
A2 A3 r  r3
=
,
A2 C
r
A2C =
2r rr3
r  r3
, C2 B =
2r rr2
r  r2
, B2A =
2r rr1
r  r1
Mit der Heron-Formel ergibt sich schließlich:
ABC = ( A2 C  B2 A  C2 B)( A2C)( B2 A)(C2 B) ,
wobei A2C = s – c, B2A = s – a und C2B = s – b ist.
Außerdem gilt weiter:
ABC =
1
r (a + b + c) = r (A2C + B2A + C2B).
2
Daraus erhalten wir folgende Gleichung:
(2r rr3 ) (2r rr1 ) (2r rr2 )
(r  r3 )
(r  r1 )
(r  r2 )
 r ²(
2r rr3
r  r3

2r rr1
r  r1

2r rr2
r  r2
),
welche letztendlich zu folgender quadratischen Gleichung führt:
r²( r1  r2  r3 )–r{ r1 r2 r3 +( r1 r2 + r2 r3 + r3 r1 )( r1 + r2 + r3 )}
+ r1 r2 r3 ( r1 r2 + r2 r3 + r3 r1 ) = 0, bzw.:
{( r1  r2  r3 )r -
r1 r2 r3 }{r – ( r1 r2 +
r2 r3 +
r3 r1 )} = 0.
Betrachtet man nun den Spezialfall, dass das gegebene Dreieck gleichseitig wird, so
sind die drei Radien ri der kleinen Kreise gleich und es gilt für den Radius des großen
Kreises: r = 3 ri, was nur von dem zweiten Term ( r1 r2 +
r2 r3 + r3 r1 ) erfüllt
34
werden kann. Da r stetig von den ri abhängt, kann aus diesem speziellen Fall auf den
allgemeinen Fall geschlossen werden.
Diese Tatsache zeigt, dass die korrekte Lösung der Gleichung für den allgemeinen
Fall folgende Beziehung für r ist:
r=
r1 r2 +
r2 r3 +
r3 r1 .
6.5 Sangaku 5
Am Ende dieses sechsten Kapitels stelle ich nun noch eine Sangaku-Aufgabe, zu der
ich jedoch keine Lösung präsentiere. Diese Aufgabe ist für diejenigen Leser gedacht,
die sich gerne einmal selbst an einem Sangaku versuchen wollen. Das Problem
stammt aus Quelle [FuPe], wo sich auch das gesuchte Ergebnis finden lässt.
Das Problem lautet folgendermaßen:
Das Dreieck ABC hat den Inkreis k(M, r). Die drei Kreise k1(M1, r1), k2(M2, r2) und
k3(M3, r3) berühren jeweils den Kreis k von außen und der Kreis k1 die Seiten des
Dreiecks AB und AC, der Kreis k2 die Seiten AB und BC und der Kreis k3 die Seiten
BC und AC.
Die drei gemeinsamen paarweisen Tangenten an diese drei Kreise bilden ein weiteres
Dreieck A`B`C`.
Gesucht ist nun der Inkreis k`(M`, r`) dieses Dreiecks A`B`C` in Abhängigkeit der
Radien r1, r2 und r3.
Folgende Skizze verdeutlicht dieses Problem:
A
M1
A`
M`
B`
C`
M2
M3
B
C
35
7 Sangakus in der heutigen Schulgeometrie
Wenn man als Student der Mathematik für das Lehramt an Realschulen eine Arbeit
über ein auf den ersten Blick schulfern erscheinendes Thema „Sangaku- Japanische
Tempelgeometrie“ verfasst, stellt man sich natürlich die Frage, ob sich dieses Thema
auch für die Verwendung im Schulunterricht eignet.
Hat man sich einmal mit dem Thema Sangaku beschäftigt und weiß, wie solche
Sangaku-Probleme aussehen, erkennt man schnell beim Betrachten einiger
Geometrie-Schulbücher, dass sich dort Geometrie-Aufgaben finden lassen, die
damaligen Sangaku-Aufgaben ähnlich sind. Auch hier werden in einen Kreis oder
Halbkreis Dreiecke einbeschrieben oder umgekehrt und es müssen Radien oder
Seitenlängen in Abhängigkeit von bekannten Größen berechnet werden.
Im Folgenden möchte ich einige solcher Schulbuchaufgaben vorstellen.
7.1 1. Beispiel aus dem Schulbuch
Diese Aufgabe stammt aus dem Buch „Anschauliche Geometrie 9“ von Barth,
Krumbacher und Ossiander [BaKO].
Folgende Aufgabe ist gegeben:
C
T
P
M
A
S
Q
B
36
Gegeben ist ein rechtwinkliges Dreieck, das zusammen mit dem Halbkreis errichtet
ist über dem Mittelpunkt der Hypotenuse mit einem Radius halb der Länge der
Hypotenuse.
Gesucht ist der Radius des größten Kreises, den man so in die Figur einbeschreiben
kann, dass dieser Kreis die Höhe des Dreiecks, die Hypotenuse und den Halbkreis
berührt.
Zunächst zeichne ich wieder einige Hilfslinien und –punkte in die Skizze mit ein:
C
90 °
T
r
P
M
A
S
H
Q
B
Es gilt zunächst:
Die Punkte S (Mittelpunkt des großen Kreises), M (Mittelpunkt des kleinen Kreises)
und T liegen stets auf einer Geraden, da T sowohl Berührpunkt an den kleinen Kreis
mit dem Radius r ist, als auch Berührpunkt an den großen Halbkreis mit dem
Radius
c
.
2
Um den Radius r des kleinen Kreises zu bestimmen, betrachte ich nun das
rechtwinklige Dreieck SQM. Dieses Dreieck ist bei Q rechtwinklig, da die
Dreiecksseite c des großen Dreiecks Tangente an den Kreis ist.
Nun müssen die Seitenlängen der drei Seiten bestimmt werden. Die Seite MQ ist
offensichtlich gleich dem Radius r des kleinen Kreises.
Die Seite SM drücke ich mit Hilfe der Strecke ST aus, wobei die Strecke ST gleich
c
dem Radius des großen Kreises ist, also ST = . Da MT offensichtlich gleich dem
2
c
Radius r ist, gilt für die Dreiecksseite SM: SM = - r.
2
37
Nun benötige ich noch die Strecke SQ. Hier gilt: = q -
c
und HQ = r. Deshalb ergibt
2
sich für die gesuchte Dreiecksseite SQ: SQ = SH + HQ = q -
c
+r.
2
Nun wende ich auf dieses rechtwinklige Dreieck den Satz des Pythagoras an, nach
dem gilt:
r² + (q -
c
c
+r)² = ( - r)².
2
2
Diesen Ausdruck vereinfache ich nun folgendermaßen:
r² + r² + 2qr - cr + q² +
1
1
c ² - qc = c ² - cr + r²
4
4
 r² + 2qr + q² - qc = 0
 r² + 2qr + q² = qc
Da nach dem Kathetensatz außerdem qc = b² gilt, ersetze ich auf der rechten Seite qc
durch b² und erhalte so:
r² + 2qr + q² = b²
Die linke Seite ist außerdem eine binomische Formel, die ich umformen kann zu:
(r + q)² = b²
Nun radiziere ich noch auf beiden Seiten:
r+q=b
Und stelle schließlich noch nach r um:
r = b – q.
Also habe ich, wie gefordert, einen Ausdruck für r gefunden.
Dies ist eine Geometrie-Aufgabe aus einem 9. Klasse-Mathematikbuch des
Gymnasiums und stellt ein verborgenes Sangaku-Problem dar. Bei dieser Aufgabe
müssen die Schüler den Satz des Pythagoras beherrschen und in der Lage sein,
geeignete Hilfslinien und Dreiecke einzuzeichnen.
38
7.2 2. Beispiel aus der Schulgeometrie
B
C
N
P
M
Q
A
D
Bei dieser Figur handelt es sich um einen Kreis, dem ein Sehnenviereck ABCD
einbeschrieben ist. Durch die Diagonalen AC und BD entstehen im Viereck Dreiecke
ABC, BCD, CDA und DAB, für die jeweils der Inkreis mit den Mittelpunkten M, N,
P und Q konstruiert wurde. Dies geschieht am einfachsten mit Hilfe der
Winkelhalbierenden.
In dieser Aufgabe ist nun zu beweisen, dass die Verbindungslinien der Mittelpunkte
M, N, P und Q der vier Inkreise ein Rechteck bilden.
Im Folgenden möchte ich einen Beweis zu dieser Behauptung liefern:
Hierfür zeichne ich in meine Aufgabenskizze noch die Punkte R, S, T und U mit ein,
welches jeweils die Schnittpunkte der vier Winkelhalbierenden des Sehnenvierecks
ABCD mit dem Viereck MNPQ sind. Vgl.[Q].
39
B
N
C
U
R
P
M
TS
Q
A
D
Es gilt zunächst:
 BCA =  BDA,
da beide die Kreissehne AB als Grundseite haben und somit der Umfangswinkelsatz
gilt.
Außerdem gilt wegen der Innenwinkelsumme im Dreieck BNA und da die Strecken
AN und BN Winkelhalbierende im Dreieck ABC sind:
 BNA = 180°-
ABC CAB
180 ABC CAB
= 90° +
2
2
2
2
2
(1)
Und im Dreieck ABC:
 BCA = 180° -  CAB -  ABC
=>
BCA 180 CAB ABC
=
2
2
2
2
(2)
Nun setzt man Gleichung (2) in (1) ein und erhält schließlich:
 BNA = 90° +
BCA
BDA
= 90° +
.
2
2
Und zudem gilt aus dem gleichen Grund im Dreieck ABD, in dem die Strecken AM
und BM Winkelhalbierende sind:
Daraus ergibt sich also:  BNA =
 BMA
= 90° +
BCA
BDA
= 90° +
.
2
2
 BMA.
Hieraus ist zu folgern, dass die Punkte ABNM des gleichnamigen Vierecks auf
einem Kreis liegen, also das Rechteck ABNM auch ein Sehnenviereck ist.
40
In einem Sehnenviereck ergeben gegenüberliegende Winkel zusammen 180°.
Daher gilt:  ABN + (  NMB +  BMA) = 180°.
Da die Punkte AMR auf einer Geraden liegen, muss der Winkel
 RMN zusammen
mit  NMB und  BMA auch 180° ergeben, weshalb  ABN =  RMN sein muss.
Ebenso führt man den Beweis für die Vierecke ADQM, DCPQ und CBNP.
Es ergibt sich also auch folgende Gleichheit:
 QDA =
 QMR.
Da in einem Sehnenviereck gegenüberliegende Winkel zusammen 180° ergeben, gilt
also:
 ABC +  CDA = 180°,
woraus sich für die Winkel, die von den Winkelhalbierenden BN und DQ begrenzt
sind, ergibt:
 NBA +  QDA = 90°,
also auch:
 RMN +
 QMR
= 90° =
 NMQ.
Dies zeigt also, dass der Winkel
 NMQ
des Vierecks MNPQ ein rechter Winkel ist.
Die gleiche Beweisführung wird für die restlichen Winkel des Vierecks MNPQ
vollzogen.
Daraus erhält man schließlich, dass alle vier Winkel des Vierecks rechtwinklig sind,
dass also das Viereck MNPQ tatsächlich ein Rechteck ist.
Vgl. [Q].
7.3 3. Beispiel aus dem Schulbuch
Dies ist eine Aufgabe aus dem Mathematikbuch für eine 10. Klasse der Realschule,
erschienen im Westermann-Verlag [DEGW]. Diese Aufgabe soll im Unterricht als
Vertiefung zur Berechung am Kreis dienen.
Sie lautet folgendermaßen:
Einem Rechteck mit der Länge a = 9 cm und der Breite b werden zwei Kreise mit
den Radien 3 cm und 2 cm wie in der folgenden Abbildung einbeschrieben:
41
b
R
P
Q
a
Ermittelt werden soll nun, wie breit das Rechteck mindestens sein muss.
a) Löse die Aufgabe durch Konstruktion.
b) Begründe, dass gilt: PQ = 1 cm.
c) Berechne die Länge PR.
d) Berechne anschließend die Breite b des Rechtecks.
e) Berechne den prozentualen Anteil der beiden Kreisflächeninhalte am
Flächeninhalt des Rechtecks.
Diese Aufgaben finden sich genauso formuliert in oben genanntem Mathematikbuch.
Durch die Hilfslinien in der Skizze, die man identisch so im Buch findet, ist die
Lösung dieser Aufgabe schon relativ weit vorgegeben.
Wären lediglich die zwei Kreise im Rechteck gegeben, würde es sich um ein echtes
Sangaku-Problem handeln, das man ebenso in Japan zur Zeit der WasanMathematik hätte finden können.
Ich werde zu dieser Aufgabe nun keine Musterlösung angeben, da der interessierte
Leser leicht auf eine eigene Lösung kommen kann. Zum Überprüfen der eigenen
Rechnung hier aber die Ergebnisse der Teilaufgaben c) – e): c) PR = 1cm,
d) b = 8cm, e) Anteil der Kreisflächen am Rechteck: 56,7 %.
42
7.4 Allgemeines zur Anwendung in der Schule
Es ist festzustellen, dass sich Sangaku-ähnliche Aufgaben relativ häufig in
Geometrieteilen von Schulbüchern finden lassen. Hauptsächlich bei Aufgaben zur
Berechnung am Dreieck und im Bereich der Kreisgeometrie werden den Schülern
häufig Aufgaben gestellt, in denen ihnen bekannte geometrische Beziehungen
versteckt sind und die sie als Vertiefung des Gelernten bearbeiten sollen.
Während meiner Recherche zu dieser Arbeit ist mir aber kein Mathematikbuch
begegnet, in dem ein Verweis auf die japanische Tempelgeometrie gegeben wird
oder in dem eine historische Sangaku-Tafel abgebildet ist, auf dem eine von Schülern
zu lösende Aufgabe zu finden ist. Meiner Meinung nach wäre es für Schüler schon
interessant zu erfahren, dass die Aufgaben, die sie bearbeiten müssen, nicht erst von
den Buchautoren und Mathematiklehrern der heutigen Zeit erfunden wurden,
sondern dass es bereits vor einigen Jahrhunderten in einem anderen Teil der Welt
Menschen gab, die sich mit solchen Problemstellungen beschäftigt haben. Auch die
Tatsache, dass solche Aufgaben bei den Japanern früher nicht als reine
Mathematikaufgaben angesehen wurden, sondern eher als eine Art „Volkssport“
betrieben wurden, könnte Schüler dazu motivieren, sich gerne mit solchen
Problemen auseinanderzusetzen und die Lust am geometrischen Knobeln zu
entdecken.
43
8 Vergleich mit der europäischen Geometrie zur WasanZeit
8.1 Allgemeine Entwicklung der europäischen Geometrie
Zu der Zeit, in der in Japan die Wasan-Mathematik entsteht, befindet sich auch die
europäische Geometrie in einer Entwicklung, in der zahlreiche neue Arten der
Geometrie ins Leben gerufen werden.
Im 17. Jahrhundert entsteht die analytische Geometrie, die vor allem von dem
französischen Philosophen und Mathematiker René Descartes geprägt ist, der 1637
das bedeutende Mathematikwerk „Discours de la méthode“ (Abhandlung über die
Methode) veröffentlicht [E]. Descartes schafft in seinem Werk die Verbindung von
Geometrie und Algebra, indem er zeigt, wie man Methoden des einen Gebietes auf
das andere anwenden kann und umgekehrt. Auf dieser Grundlage der analytischen
Geometrie werden geometrische Figuren durch algebraische Ausdrücke dargestellt,
also Gleichungen dazu verwendet, um Figuren auszudrücken.
Eine weitere wichtige Entdeckung des 17. Jahrhunderts stellt die projektive
Geometrie dar. Hier werden Eigenschaften geometrischer Figuren untersucht, die
sich nicht ändern, wenn die Figuren von einer Ebene auf eine andere Ebene projiziert
werden [M]. Mit Hilfe der projektiven Geometrie können zum Beispiel die
verschiedenen Kegelschnitte durch geeignete Projektion ineinander übergeführt
werden.
Im 18. Jahrhundert wird schließlich noch die Differentialgeometrie entwickelt, die
die Geometrie mit der Analysis verbindet [Ma].
In diesen Gebieten entdecken verschiedene europäische Mathematiker Lehrsätze und
Beweise, die eine enorme Bedeutung für die heutige Mathematik haben. Deshalb ist
zum einen über diese westliche Mathematik wesentlich mehr bekannt als über
Wasan, zum anderen sind dies oft Entdeckungen, die heute Grundlagen der Schulund Universitäts-Geometrie sind.
44
8.2 Die Inversions-Methode
Die Inversion, auch genannt Kreisspiegelung bzw. Spiegelung am Kreis ist eine
spezielle Abbildung der ebenen Geometrie, die das Innere und das Äußere eines
gegebenen Kreises miteinander vertauscht.
Für die Kreisspiegelung an einem Kreis mit dem Mittelpunkt M und Radius r ist der
Bildpunkt P` eines Punktes P dadurch festgelegt, dass P` auf der Halbgeraden [MP
liegen und die Bedingung MP `
r²
erfüllen muss.
MP
Die Inversion ist eine Methode, mit der man einige Sangaku-Probleme ganz kurz und
einfach lösen kann. Diese Methode war jedoch bei den japanischen Mathematikern
dieser Zeit nicht bekannt, so dass viele Aufgaben eine viel längere und
kompliziertere Lösung erforderten. Vgl. [FuPe] und [P].
8.3 Der Satz von Descartes
Der Satz von Descartes, der nach René Descartes (1596-1650) benannt ist, beschreibt
eine Beziehung zwischen vier Kreisen, die einander berühren. Dieser Satz, der auch
als „Vier-Kreise-Satz von Descartes“ bezeichnet wird, macht es möglich, zu drei
gegebenen Kreisen, die einander wechselseitig berühren, einen vierten Kreis zu
finden, der die drei anderen Kreise berührt [I].
Dieses Problem war auch in der Wasan-Mathematik in Japan Gegenstand einer
Sangaku-Aufgabe. Hier handelte es sich jedoch nicht um Kreise, sondern um Kugeln
im dreidimensionalen Bereich. Folgende Skizze stellt das Problem dar:
45
Im Folgenden möchte ich eine moderne Lösung für den verallgemeinerten
n-dimensionalen Raum vorstellen und im Anschluss daran eine original japanische
Lösung, für jene Leser, die die japanische Sprache beherrschen bzw. für alle die, die
sich für fremde Kulturen interessieren.
8.3.1 Lösung im n-dimensionalen Fall
Bei dieser Lösung orientiere ich mich an der Quelle [K].
Im n-dimensionalen Raum sind n + 2 Kugeln mit den Radien r1, r2, …, rn+2 gegeben
und es sei ki =
1
mit i = 1, 2, …, n + 2.
ri
Dann gilt: n (k1² + k2² + … + kn+2²) = (k1 + k2 + … + kn+2)²,
wenn die Kugeln sich einander von außen her berühren.
46
Lösung:
Zum Lösen dieser Aufgabe wird die Theorie der Determinanten verwendet. Zur
Vereinfachung werden im (n – 1)-dimensionalen Raum n + 1 sich einander von
außen berührende Kugeln untersucht. Die Radien der Kugeln sind dabei r0, r1, …, rn.

Mit a ij wird der Vektor bezeichnet, der die Mittelpunkte der Kugeln i und j

verbindet, d. h. aij = aij = ri + rj.

 
Durch Quadrieren der Vektorgleichung a ij = a 0 j - ai 0 ergibt sich für das
Skalarprodukt:
 
1
a 0i  a 0 j = (a0i²+ a0j² – aij²)
2
(1)
Die n Vektoren a01, a02, …, a0n, in einem n-dimensionalen Raum sind linear
abhängig. Hieraus ergibt sich, dass ihre Gramsche Determinante gleich Null ist. Das
bedeutet:
 
a01  a01
 
a02  a01

 
a0 n  a01
 
a01  a02
 
a02  a02

 
a0 n  a02




 
a01  a0 n
 
a02  a0 n
= 0.

 
a0 n  a0 n
Hier setzen wir nun (1) ein und multiplizieren dabei jede Zeile mit 2, damit die
Brüche wegfallen. Daraus ergibt sich:
2a01 ²
a01 ²  a02 ²  a12 ²
a ²  a02 ²  a12 ²
2a02 ²
Dn := 01


a01 ²  a0 n ²  a1n ² a02 ²  a0 n ²  a 2 n ²
 a01 ²  a0 n ²  a1n ²
 a02 ²  a0 n ²  a 2 n ²
= 0.



2a 0 n ²
Diese Gleichung ist gleich der Determinante (n + 2)–ten Grades, welche man durch
Entwicklung nach der letzten Zeile und letzten Spalte erhält:
47
a 01 ²  a 0 n ² 1
0
a ²
0
01
~
D n+2:= 
(Dn)
 = 0,
0
a0n ²
1

0
0
0
wobei der mittlere Teil, der eingerahmt ist, die zur Determinante Dn gehörende
Matrix ist.
Anschließend wird nun die erste Zeile von jeder anderen Zeile außer der letzten Zeile
subtrahiert und man erhält:
0
a 01 ²
a 01 ²
a 01

a0 n ² a0 n
1
2
2

a0 n ²
 a01  a1n ²  1


 a1n ² 
a0 n

0
0
1
2

2
 = 0.
1
0
Nun wird ebenso die erste Spalte von jeder anderen Spalte außer der letzten
subtrahiert. Hieraus ergibt sich, wenn man zusätzlich die Vorzeichen umdreht:
0
a 01 ²  a 0 n ² 1
a 01 ²
0
 a1n ² 1



a 0 n ² a1n ² 

0
 = 0.
1
1
1

1
0
Nun werden die i-te Zeile mit ki² und die j-te Zeile mit kj² multipliziert, wobei
i, j = 0, 1, …, n ist. Dieser Schritt ist möglich, da sich die Determinante nicht ändert,
wenn zeilenweise mit einem Skalar multipliziert wird.
Dabei entstehen die Terme aij ²  k i ² k j ² = (ri + rj)²ki²kj² = (
1 1
 )²ki²kJ² = (ki+ kj)²
ki k j
und es ergibt sich die Determinante:
48
(k 0  k1 )²  (k 0  k n )² k 0 ²
0
(k 0  k1 )²

 (k1  k n )²


0

(k 0  k n )² (k1  k n )² 
k0 ²

k1 ²
k1 ²
 = 0.
0
kn ²
kn ²
0
Im nächsten Schritt wird die letzte Zeile von allen anderen Zeilen subtrahiert:
 k0
k 0 ²  2 k 0 k1
2
2 k 0 k1  k1 ²
 k1


2 k 0 k n  k n ² 2 k1 k n  k n ²
k0 ²
k1 ²
2
 k 0  2k 0 k n
2
 k 1  2 k1 k n


2

 kn

kn ²
2
k0 ²
k1 ²
 = 0.
kn ²
0
Jetzt wird noch die letzte Spalte von allen anderen Spalten subtrahiert. Anschließend
verdoppelt man die letzte Zeile und die letzte Spalte, woraus sich schließlich ergibt:
 2k 0 ²
2k 0 k1
2k 0 k1

 2k1 ² 


2k 0 k n
2k1 k n
  2k n ² 2k n ²
2k 0 ²
2k1 ²

 2k 0 k n
2k1 k n

2k n
2k 0 ²
2k1 ²
 = 0.
0
Nun wird die i-te Zeile durch ki und die j-te Spalte durch kj dividiert,
mit i, j = 0, 1, …, n-1 und außerdem mit 2 gekürzt. Dies ist wieder möglich, da sich
die Determinante nicht ändert, wenn man durch ein Skalar dividiert.
Daraus erhält man nun folgende Matrix:
1
1

1
k0
1

1 
 
1

k1
 = 0.
1
1
  1 kn
k0
k1
 kn
(1)
0
49
Diese Gleichung hat die Form:
Pn (k0² + k1² + …+ kn²) + 2Qn (k0k1 + k0k2 + … + kn-1kn) = 0, mit
1
1
1

1
1
1
1
1

1
1 1
Pn:= - 1

1

1 
 
1
1
1
1 und Qn:= 1


 1
1
1
1

1
1

1
1

1 
 
1
1
1 .

 1
Dies ergibt sich durch Entwicklung der Determinante (1) nach der letzten Zeile und
der letzten Spalte.
Nun ist noch zu zeigen, dass Pn = -(n - 2)Qn ist:
Addiert man zur ersten Zeile in Pn alle anderen Zeilen, dann wird jedes Element der
ersten Zeile gleich n – 2. Ebenso geht man in den anderen Zeilen vor.
Hieraus folgt schließlich mit den vorausgegangenen Überlegungen:
(n – 2) (k0² + k1² + … + kn²) = 2 (k0k1 + k0k2 + kn-1kn)
Nach Umformen erhält man schließlich die Behauptung:
(n – 1) (k0² + k1² + … + kn²) = (k0 + k1 + … + kn)².
Und somit ist die Aussage für den n-dimensionalen Raum gezeigt und kann jetzt z.B.
auf den dreidimensionalen Raum mit 5 Kugeln angewendet werden, wofür sich dann
ergibt: 3(k1² + k2² + k3² + k4² + k5²) = (k1 + k2 +k3 +k4 + k5)².
8.3.2 Original japanische Lösung
Diese Lösung ist zu finden im Buch „Japanese Temple Geometry Problems: San
Gaku“ von Fukagawa und Pedoe [FuPe], auf den Seiten 179-186.
50
51
52
53
54
55
56
57
58
9 Schlusswort
Die japanische Wasan-Mathematik ist ein Bereich, dem kaum Beachtung geschenkt
wird. Dies liegt, wie oben aufgeführt, vor allem daran, dass aus dieser Kultur kaum
bekannten Lehrsätze hervorgegangen sind. Während der Beschäftigung mit diesem
Thema wurde mir aber klar, dass es schade ist, dass darüber so wenig bekannt ist.
Die Sangaku-Tafeln sind häufig mit so interessanten und eleganten Problemen
kunstvoll bemalt, dass sie regelrecht zum Knobeln anregen. Es wird immer wieder
deutlich, dass die Beschäftigung mit Sangakus nicht nur Mathematik war, sondern
auch stets großer Wert auf den künstlerischen Aspekt gelegt wurde. Ein Zitat von
Tony Rothman drückt meiner Meinung nach die Begeisterung und Faszination für
diese mathematische Tradition besonders gut aus und bildet deshalb das Schlusswort
meiner Arbeit:
„ Of the world`s countless customs and traditions, perhaps none is as elegant, nor as
beautiful, as the tradition of sangaku, Japanese temple geometry. “ [N]
59
10 Literaturverzeichnis

[FuPe] H. Fukagawa und D. Pedoe: “Japanese Temple Geometry Problems:
San Gaku”, erschienen 1989 in Winnipeg, Kanada, veröffentlicht von: The
Charles Babbage Research Center Winnipeg

[ScSc] C. J. Scriba und P. Schreiber: “5000 Jahre Geometrie –Geschichte,
Kulturen, Menschen ”, erschienen im Springer-Verlag

[FuRo] H. Fukagawa und Tony Rothman: „Sangaku – Japanische
Tempelgeometrie“, aus: Spektrum der Wissenschaft 7/ 1998, Seite 80 ff.

[Ped] Dan Pedoe: „A course of Geometry for colleges and universities”,
Cambridge at the university press, 1970

[BaKO] Barth, Krumbacher, Ossiander: „Anschauliche Geometrie 9“,
erschienen im Ehrenwirth-Oldenbourg- Verlag

[DEGW] J. Dlugosche, C. Englmaier, F. Götz, J. Widl: „Mathematik 10 II,
III, Realschule Bayern“, erschienen im Westermann- Verlag, 2005
Braunschweig

[Ma] Klaus Mainzer: „Geschichte der Geometrie“, erschienen 1980,
Mannheim, Wien, Zürich: Bibliographisches Institut

[BMNW] Barth, Mühlbauer, Nikol, Wörle: „Mathematische Formel und
Definitionen“, erschienen im Bayerischen Schulbuch-Verlag, J. Lindauer
Verlag (Schaefer), 7. Auflage von 1998

[Ste] Milorad R. Stevanovic: „Triangle Centers Associated with the Malfatti
Circles”, erschienen in Forum Geometricum, Volume 3 (2003), Seite 83-93.
60

[A1] N.N.: „Seki Takakazu“, zu finden unter:
http://de.wikipedia.org/wiki/Seki_Takakazu, Stand: 31.10.1007

[A2] J. O`Connor and E. F. Robertson: “Takakazu Seki Kowa”, zu finden
unter: http://turnbull.mcs.st-and.ac.uk/~history/Printonly/Seki.html,
Stand: 24.10.2007

[B] Ingmar Rubin: „Sangaku – Probleme“, Berlin, zu finden unter:
http://www.matheraetsel.de/lit_geometrie.html, sangaku.pdf,
Stand 27.10.2007

[C] Chad Boutin: „Rothman helps reveal intricacies of ancient math
phenomenon”, zu finden unter:
http://www.princeton.edu/main/news/archive/S15/04/04077/index.xml,
Stand 12.09.2007

[D]
N.N.:
“Clickable
Sangaku
Map”,
zu
finden
unter:
http://www.wasan.jp/english/map.gif, Stand: 18.03.2007

[E] N.N.: „Geschichte der Geometrie – Die Neuzeit“, zu finden unter:
http:// www.oliver-bieri.ch/mascheroni/geschicht_neuzeit.html,
Stand: 12.09.2007

[F] „Malfatti's Problem“, zu finden unter:
http://www.cut-the-knot.org/Curriculum/Geometry/Malfatti.shtml,
Stand: 18.12.1007

[G] „Malfatti Circles“, zu finden unter
http:// mathworld.wolfram.com/MalfattiCircles.html, Stand 18.12.2007

[H ] „Casey`s Theorem“, zu finden unter
http:// mathworld.wolfram.com/CaseysTheorem.html, Stand 18.12.2007
61

[I] „Satz von Descartes“, zu finden unter
http://de.wikipedia.org/wiki/Satz_von_Descartes, Stand 13.12.2007

[K] Oleg Faynshteyn: „Berührende Kreise und Kugeln in: „Die Wurzel“,
Zeitschrift für Mathematik, Heft 07/02

[L] N.N. „Pierre de Fermat“, zu finden unter
http://www.uni-essen.de/didmath/texte/jahnke/quellen/fermatpascal01.html,
Stand 13.12.2007

[M] “Mathematik und die wissenschaftliche Revolution”, zu finden unter:
http://www.mathematik.de/mde/information/matheInGeschichteUndGegenw
art/jahrtausende/kapitel7.html, Stand 19.11.2007

[N] N. N. “Sangaku: Reflections on the Phenomenon”, zu finden unter
http://cut-the-knot.org/pythagoras/Sangaku.shtml, Stand 18.03.2007

[O] N. N, „Ähnlichkeitssätze“, zu finden unter
http://de.wikipedia.org/wiki/Ähnlichkeitssätze , Stand 19.11.2007

[P] N.N. “Inversion”, zu finden unter:
http://de.wikipedia.org/wiki/Inversion_(Geometrie), Stand 19.11.2007

[Q] Antonio Gutierrez: „Sangaku Japanese Geometrical Problem“, zu finden
unter: http://agutie.homestead.com/files/sangaku2.html, Stand 18.03.2007
Danksagung:
Mein Dank gilt besonders Herrn Prof. Dr. Steuding, der immer ein offenes Ohr für
meine Fragen hatte und mich stets mit hilfreicher Literatur versorgt hat.
62
Erklärung:
Hiermit versichere ich, dass ich die Arbeit in allen Teilen selbstständig angefertigt
habe und keine anderen als die in der Arbeit angegebenen Hilfsmittel benutzt habe.
Die Zeichnungen und bildlichen Darstellungen habe ich selbst angefertigt.
Würzburg, den 29.02.2008
Christiane Hartmann
63