Repetition deutliche Sehbereiche

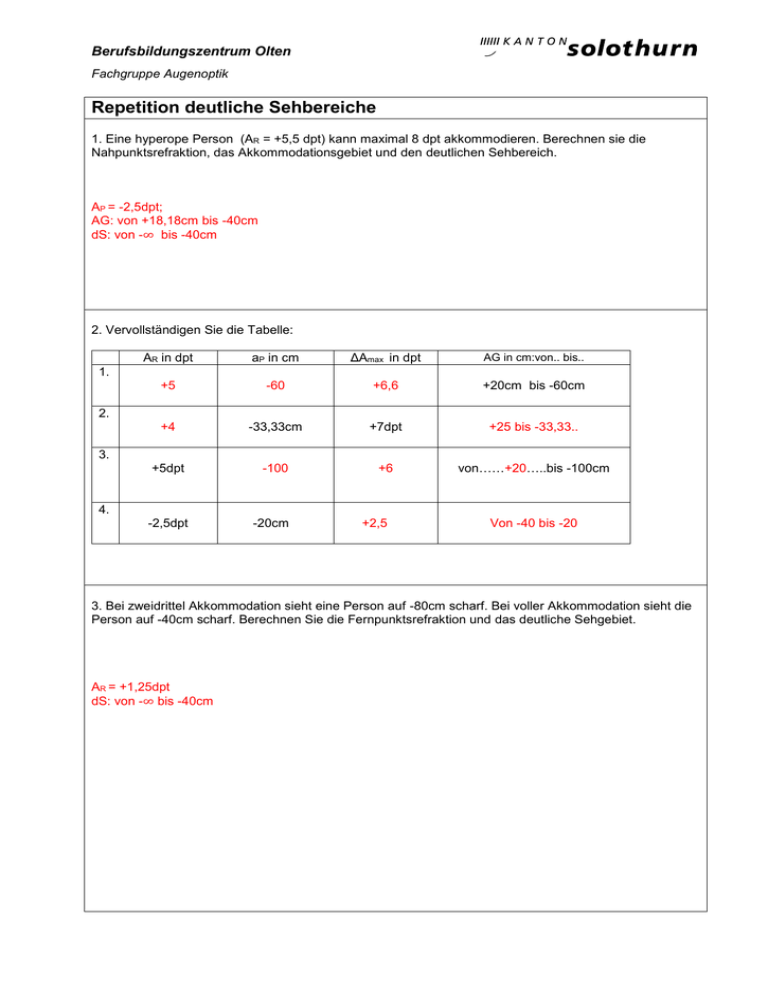
Berufsbildungszentrum Olten
Fachgruppe Augenoptik
Repetition deutliche Sehbereiche
1. Eine hyperope Person (AR = +5,5 dpt) kann maximal 8 dpt akkommodieren. Berechnen sie die
Nahpunktsrefraktion, das Akkommodationsgebiet und den deutlichen Sehbereich.
AP = -2,5dpt;
AG: von +18,18cm bis -40cm
dS: von -∞ bis -40cm
2. Vervollständigen Sie die Tabelle:
AR in dpt
aP in cm
ΔAmax in dpt
AG in cm:von.. bis..
+5
-60
+6,6
+20cm bis -60cm
+4
-33,33cm
+7dpt
+25 bis -33,33..
+5dpt
-100
+6
von……+20…..bis -100cm
-2,5dpt
-20cm
1.
2.
3.
4.
+2,5
Von -40 bis -20
3. Bei zweidrittel Akkommodation sieht eine Person auf -80cm scharf. Bei voller Akkommodation sieht die
Person auf -40cm scharf. Berechnen Sie die Fernpunktsrefraktion und das deutliche Sehgebiet.
AR = +1,25dpt
dS: von -∞ bis -40cm
4. Bei der Hälfte der max. Akkommodation sieht eine Person auf -40cm scharf. Bei voller Akkommodation
sieht die Person auf -20cm scharf. Berechnen Sie die Fernpunktsrefraktion und das deutliche Sehgebiet.
AR = +0dpt
dS: von -∞ bis -20cm
5. Ein +5,0dpt hyperopes Auge kann maximal +9,0dpt akkommodieren. Berechnen Sie das deutliche
Sehgebiet dieser Person.
dS: von -∞ bis -25cm
6. Der Nahpunkt eines kurzsichtigen Auges ist 12,5cm vor dem Auge. Der Einstellpunkt liegt bei halber
Akkommodation 20 cm vor dem Auge. Wie lautet die Fernpunktsrefraktion dieser Person?
AR = -2,0dpt
7. Wenn eine Person nur einen Drittel seiner Akkommodation benutzt, sieht sie auf -100cm scharf. Würde
die Person voll akkommodieren, so sähe sie auf -0,4m scharf.
Berechnen Sie die Fernpunktsrefraktion.
AR = -0,25dpt
8. Eine Person ist 6dpt kurzsichtig und kann maximal 3dpt akkommodieren. Berechnen Sie den
maximalen deutlichen Sehbereich dieser Person ohne Brille.
dS: von -16,66..cm bis -11,11..cm
9. Der Nahpunkt bei einem Auge liegt bei -10cm. ∆Amax ist 12dpt. Berechnen Sie die Fernpunktsrefraktion
und den deutlichen Sehbereich.
AR = +2,0dpt
dS: von -∞ bis -10cm
10. Ein Kunde (AR= +3,75dpt; ΔAmax= 2,5dpt) trägt eine Trifokalbrille mit folgenden Werten:
Ferne: +4,25dpt; Addition: 2,5dpt
Bestimmen Sie die deutlichen Sehbereiche mit dieser Brille für die Ferne, den Zwischenteil und die Nähe.
Rechnen Sie dabei jeweils mit ½ ΔAmax.
Ferne: dS von -2m bis -57,14cm
Zwischenteil: dS von -57,14cm bis -33,33..cm
Nahteil: dS von -33,3..cm bis -23,5cm
11. Ein Kunde (AR= +4,5dpt; ΔAmax= 2,5dpt) trägt eine Gleitsichtbrille mit folgenden Werten:
Ferne: +5,25dpt; Addition: 2,5dpt
Bestimmen Sie den deutlichen Sehbereich mit dieser Brille. Rechnen Sie dabei mit voller ΔAmax.
dS von -1,33..m bis -17,4cm
12. Ein Kunde (AR= -3,0dpt; ΔAmax= 5,5dpt) trägt eine Einstärkenbrille mit folgendem Wert:
Ferne: -3,5dpt;
Bestimmen Sie den deutlichen Sehbereich mit dieser Brille. Rechnen Sie dabei mit voller ΔAmax.
dS von -∞ bis -20cm
13. Eine Person (AR = +12,5dpt; ∆Amax = +3dpt) trägt eine Brille, welche für einen HSA von 10,9mm
berechnet wurde, in einem HSA von 15mm. Berechnen sie das deutliche Sehgebiet in dieser Situation.
VKHSA 10,9 = +11,0dpt
VKHSA 15 = +10,5dpt
dS von -2m bis -28,57cm
14. Zeichnen Sie die Vollkorrektionsbedingung bei einer AR = -10,0dpt, wenn das Brillenglas in einem HSA
von 20mm ist. Beschriften Sie alle Strecken. Wie stark muss das vollkorrigierende Brillenglas sein?
15. Zeichnen Sie die Vollkorrektionsbedingung bei einer AR = +12,5dpt, wenn das Brillenglas in einem
HSA von 20mm ist. Beschriften Sie alle Strecken. Wie stark muss das vollkorrigierende Brillenglas sein?
16. Ein Versicherungsmakler (Alter 42 Jahre, ∆Amax =4,5dpt) trägt seit Jahren folgende Einstärkenbrille:
Rechts
Links
Bisher
Sph
Cyl
+3,5
+3,5
A
Add
Prisma
Seit längerem hat er bei den Büroarbeiten Mühe beim Lesen.
Sein Augenarzt stellt im folgendes Rezept aus (Vollkorrektion):
Rechts
Links
neu
Sph
+4,0
+4,0
Cyl
A
Add
1,5
1,5
Prisma
Berechnen sie seine deutlichen Sehbereiche (Rechnen Sie mit ½ ∆Amax)
a)
b)
c)
d)
Ohne Brille
Mit alter Fernbrille
Mit neuer Gleitsichtbrille
Mit neuer Computerbrille (+5,5dpt; Degression 1,0dpt)
a)
b)
c)
d)
Kein deutlicher Sehbereich
dS von -∞ bis -57cm
dS von -∞ bis -26,66..cm
dS von -2m bis -26,66..cm
17. Ein Versicherungsmakler (alter 46 Jahre, ∆Amax =2,5dpt) trägt seit Jahren folgende Einstärkenbrille:
Rechts
Links
Bisher
Sph
Cyl
-1,75
-1,75
A
Add
Prisma
Seit längerem stört es ihn aber beim Kundenkontakt ständig seine Brille beim Lesen abzuziehen und in die
Ferne wieder anzuziehen.
Sein Augenarzt stellt im folgendes Rezept aus (Vollkorrektion):
neu
Rechts
Links
Sph
-2.0
-2.0
Cyl
A
Add
1,75
1,75
Prisma
Berechnen sie seine deutlichen Sehbereiche (Rechnen Sie mit ½ ∆Amax)
a)
b)
c)
d)
Ohne Brille
Mit alter Fernbrille
Mit neuer Gleitsichtbrille
Mit neuer Computerbrille (-0,25dpt; Degression 1,0dpt)
a)
b)
c)
d)
dS von -0,5m bis -30,8cm
dS von -4m bis -66,66..cm
dS von -∞ bis -33,33..cm
dS von -1,33..m bis -33,33..cm
18. Eine myope Person (AR rechts und links -2,0dpt) trägt die Trifokalbrille seiner Zwillingsschwester mit
folgenden Werten:
R+L: sph: -2,5dpt Add: 2,5.
Seine Akkommodationsbreite beträgt 1,0dpt. Berechnen Sie die deutlichen Sehbereiche durch Fern-,
Zwischen- und Nahteil bei Verwendung der vollen Akkommodation.
Fernteil:
von unendlich bis -2m
Zwischenteil:
von -1,333m bis -0,5714m
Nahteil:
von – 0,5m bis -0,333m
19. Ein kurzsichtiger hat seinen Nahpunkt (P) in 20cm vor den Augen. Sein maximaler
Akkommodationserfolg beträgt 3dpt. Berechnen Sie dessen deutlichen Sehbereich ohne Korrektion bei
Dauerleistung (1/2ΔAmax).
AP= - 0,2m
AP= -5,0dpt
ΔAmax= AR - AP
AR= ΔAmax + AP = +3,0dpt + (-5,0dpt)= - 2,0dpt.
AE = AR – 1/2ΔAmax = -2,0dpt - 1,5dpt = - 3,5dpt
Deutliches Sehgebiet: von -0,5m bis -0,2857m
20. Um welche Astigmatismusart handelt es sich bei untenstehendem Beispiel. Machen Sie ein konkretes
Beispiel dazu.
Zusammengesetzter myoper Astigmatismus gegen die Regel
Bsp: sph: -1,0 cyl: -1,0 Axe 90°; zusammengesetzter kurzsichtiger Astigmatismus gegen die Regel.
21. Um welche Astigmatismusart handelt es sich bei untenstehendem Beispiel. Machen Sie ein konkretes
Beispiel dazu.
Sph: +2,0dpt cyl: -4,0dpt axe 0° ;
Gemischter Astigmatismus mit der Regel
22. Zeichnen sie einen zusammengesetzten Astigmatismus gegen die Regel ein:
Beispiel: sph: +4,0 dpt cyl -2,0dpt 90°