Robert Andrews Millikan (1868-1953) war ein amerikanischer

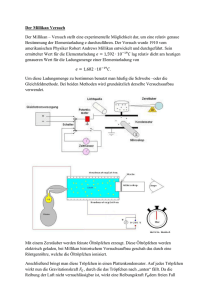
Millikan – Bestimmung der Elementarladung
Robert Andrews Millikan (1868-1953) war ein amerikanischer Physiker, der winzige Ladungen von
kleinen Öltröpfchen im Jahre 1910 und dabei erstmals die Ladung eines Elektrons bestimmt hat.
Millikan-Versuch:
In einem elektrischen Feld erfahren geladene Körper eine Kraft F, die von der elektrischen Feldstärke
E und der Ladung Q des Körpers abhängig ist. Ist die Feldstärke bekannt, kann die Kraft gemessen
werden und die Ladung des Körpers ermittelt werden.
F = QE
Q = F/E
Zwischen zwei horizontalen Platten eines luftgefüllten Plattenkondensators werden Öltröpfchen
eingesprüht. Beim Einsprühen werden die Tröpfchen durch Reibung leicht geladen. Durch ein
Mikroskop mit eingebauter Skala und seitliche Beleuchtung kann das Verhalten der Öltröpfchen im
elektrischen Feld beobachtet werden. Beim Anlegen einer Spannung steigen oder sinken die
Tröpfchen je nach Stäke des elektrischen Feldes und der Ladung der Tröpfchen unterschiedlich
schnell. Durch die Luftreibung ist die Geschwindigkeit nach kurzer Zeit konstant. Um die Tröpfchen in
die Schwebe zu bringen, muss die Spannung verändert werden. Zum Auswerten muss die Spannung
notiert werden. Anschließend kann die Spannung abgeschaltet werden, um mithilfe der Skala in dem
Mikroskop und einer Stoppuhr die Sinkgeschwindigkeit der Tröpfchen ermitteln zu können.
Um die Ergebnisse aus dem Experiment auswerten zu
können, wird eine Gleichung benötigt:
Bei Tröpfchen die sich in der Schwebe befinden sind die
elektrische Kraft Fel und die Gewichtskraft FG gleich groß:
Fel = Fg
Also gilt: qE = qU0/d = mg
𝑑
𝑞 =𝑚∙𝑔∙𝑈
0
Die Masse m eines kugelförmigen Tröpfchens mit dem Radius
r ergibt sich aus der Dichte ρ des Öls:
4
m = 𝑉 ∙ 𝜌 = 3 𝜋𝑟 3 ∙ 𝜌
Damit gilt:
4
3
q = 𝜋𝑟 3 ∙ 𝜌 ∙ 𝑔 ∙
𝑑
𝑈0
(1)
Nach Abschalten der Spannung sinkt das Tröpfchen mit der konstanten Geschwindigkeit v und dann
sind die Reibungs kraft und die Gewichtskraft gleich groß. Für die Reibungskraft gilt dabei
FR = 6𝜋ηvr mit der Viskosität der Luft η. Aus FR = FG folgt:
4
6πη∙ 𝑣 ∙ 𝑟 = 𝑚 ∙ 𝑔 = 3 𝜋𝑟 3 ∙ 𝜌 ∙ 𝑔
Durch Umformen erhält man den Radius r:
9 𝜂∙𝑣
r = √2 𝜌∙𝑔
(2)
Einsetzen von Gleichung (2) in Gleichung (1) führt auf:
3
q=
𝑑∙𝜂2
9√2𝜋 𝑈 𝜌∙𝑔
0√
3
∙ 𝑣2
Mithilfe dieser Gleichung kann die Ladung eines Tröpfchens mit messbaren Größen bestimmt
werden. Die Ladung q ist stets ein ganzzahliges Vielfaches einer Ladung e. Millikan hat diese
sogenannte Elementarladung mit e = 1,602∙ 10−19 C erstmals bestimmen können.
Die Ladung eines Elektrons ist -e und positiv und negativ geladene Körper enthalten ganzzahlige
Vielfache der Elementarladung e. Die Elementarladung ist die kleinste in der Natur vorkommende
Ladung.