Elementargeometrie

Elementargeometrie
(Skriptum von Prof. Dr. H. Möller, Pdf-Version 1 vom 11.2.02)
1
Einleitung
Die Geometrie ist das älteste und umfangreichste Teilgebiet der Mathematik. Bereits
die Ägypter und Babylonier vor mehr als 3000 Jahren entdeckten geometrische
Zusammenhänge bei der Bewältigung von Alltagsproblemen.
Aber erst ungefähr 600 v. Chr. entstand in Griechenland die wissenschaftliche Disziplin der Mathematik. Diese Leistung wurde von “Schülern” von Thales, der eigentlich Kaufmann war, und von Pythagoras erbracht, deren Namen auch im heutigen
Geometrieunterricht mit geometrischen Sätzen verbunden sind.
Ein besonders glücklicher Umstand für die Entwicklung der Mathematik war es, dass
der griechische Mathematiker Euklid († ca. 300 v. Chr.) in dem Werk “Die Elemente” das damalige mathematische Wissen über Geometrie, Arithmetik und Zahlentheorie in einer Form aufschrieb, die bis zum Beginn dieses Jahrhunderts Maßstäbe
gesetzt hat. Insbesondere geht auf ihn die “axiomatische Methode” zurück, bei der
die gesamte Theorie aus wenigen Grundsätzen (von ihm Postulate und Axiome
genannt) “deduziert” wird.
Obwohl es nach dem Niedergang der griechischen Mathematik um 200 n. Chr. und
der “mathematischen Abstinenz” der Römer fast 1000 Jahre gedauert hat, bis durch
das Werk “liber abaci” (1202) des italienischen Kaufmanns Fibonacci (= Leonardo
von Pisa) die “abendländische Mathematik” begann, blieben “Die Elemente” von
Euklid noch mehr als vierzig Generationen lang Grundlage für den Mathematikunterricht aller damaligen Bildungseinrichtungen.
Das von dem Biologen E. Häckel (um 1890) formulierte “biogenetische Grundgesetz”, demzufolge das lernende Individuum in seiner geistigen Entwicklung im
“Zeitraffer” dieselben Phasen durchläuft, wie die Menschheit, wurde von dem bekannten Mathematiker Felix Klein seit Beginn des zwanzigsten Jahrhunderts auch
auf den Mathematikunterricht übertragen. Seit Mitte der sechziger Jahre hat nun
eine ökonomisch motivierte Entwicklung den Mathematikunterricht entscheidend
verändert. Sie stützt sich auf eine neue Form der “Axiomatik”, die in dem Werk
“Grundlagen der Geometrie” (1899) von David Hilbert eingeführt wurde.
2
Ein kurzer Blick in die Geschichte der Geometrie
Wegen der Bedeutung für die Schulgeometrie in den letzten 30 Jahren betrachten
wir zunächst Anfangs- und Endpunkt des gewaltigen Bogens von Euklid bis Hilbert.
“Die Elemente” (gr.: stoichaia = Anfangsgründe) umfassen 13 “Bücher”, die das
damalige Wissen über ebene Geometrie (6 Bücher), Arithmetik (4 Bücher) und
räumliche Geometrie (3 Bücher) wiedergeben. Das erste Buch beginnt mit einer
1
Zusammenstellung von 23 “Definitionen”, 5 “Postulaten” und 9 “Axiomen”, wobei alle drei Begriffe ihre Bedeutung inzwischen geändert haben. Die ersten fünf
Definitionen lauten:
1. Ein Punkt ist, was keine Teile hat,
2. Eine Linie breitenlose Länge.
3. Die Enden einer Linie sind Punkte.
4. Eine gerade Linie (Strecke) ist eine solche, die zu den Punkten auf ihr gleichmäßig
liegt.
5. Eine Fläche ist, was nur Länge und Breite hat.
Es fällt auf, dass in jeder Definition Begriffe auftreten, die selbst nicht erklärt sind,
deren Bedeutung also von der Umgangssprache übernommen wird. Obwohl Euklid
keine Angaben über die Entstehung seiner Begriffe macht, können wir doch annehmen, dass sie das Ergebnis eines etwa 200 Jahre währenden Prozesses sind. Ähnliche
Prozesse werden heute - dem “biogenetischen Gesetz” folgend - im “empirischen”
Geometrieunterricht durchlaufen, auf den wir im vierten Kapitel eingehen.
Von den Postulaten seien im folgenden die ersten beiden und das fünfte wiedergegeben.
“Gefordert soll sein:
1. dass man von jedem Punkt nach jedem Punkt die Strecke ziehen kann,
2. dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann,
...
5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt,
dass immer auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins Unendliche sich treffen
auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind.”
Bei Hilbert werden entsprechende Aussagen “Axiome” heißen, während die Axiome
von Euklid Gleichheit, Ungleichheit, Doppeltes und Halbes betreffen, z. B.:
“1. Was demselben gleich ist, ist auch einander gleich.”
Die ersten drei geometrischen Aussagen betreffen grundlegende “Konstruktionen”,
die gleich verwendet werden, einen Kongruenzsatz zu beweisen. Mit Hilfe dieses
Kongruenzsatzes (SWS) wird dann der “Basiswinkelsatz” (im gleichschenkligen
Dreieck sind die Winkel an der Grundlinie einander gleich) hergeleitet. Dieser Satz
wird auch in der empirischen Geometrie unseres vierten Kapitels eine besondere
Rolle spielen.
Die Entwicklung der Mathematik in der zweiten Hälfte des neunzehnten Jahrhunderts mit der Entstehung der Mengenlehre (G. Cantor) und der Klärung der Logik
(G. Frege, B. Russell) ermöglichte es David Hilbert, das Problem der unklaren und
nur teilbestimmten Begriffe bei Euklid in radikaler Weise zu lösen. Mit der Methode
der Algebra, Variablen durch Relationen zu verknüpfen, beschreibt er die geometrischen Grundbegriffe nicht mehr inhaltlich, sondern nur noch durch Beziehungen
(Axiome). Im Folgenden zitieren wir seine fünf Axiomgruppen.
3
Die Axiome der Geometrie von D. Hilbert
Erstes Kapitel.
Die fünf Axiomgruppen.
§1. Die Elemente der Geometrie und die fünf Axiomgruppen.
2
Erklärung. Wir denken drei verschiedene Systeme von Dingen: die Dinge des ersten
Systems nennen wir Punkte und bezeichneten sie mit A, B, C, . . .; die Dinge des
zweiten Systems nennen wir Geraden und bezeichnen sie mit a, b, c, . . .; die Dinge
des dritten Systems nennen wir Ebenen und bezeichnen sie mit α, β, γ, . . .; die
Punkte heißen auch Elemente der linearen Geometrie, die Punkte und Geraden
heißen die Elemente der ebenen Geometrie, und die Punkte, Geraden und Ebenen
heißen die Elemente der räumlichen Geometrie oder des Raumes.
Wir denken die Punkte, Geraden, Ebenen in gewissen gegenseitigen Beziehungen
und bezeichnen diese Beziehungen durch Worte wie “liegen”, “zwischen”, “kongruent”; die genaue und für mathematische Zwecke vollständige Beschreibung dieser
Beziehungen erfolgt durch die Axiome der Geometrie.
Die Axiome der Geometrie können wir in fünf Gruppen teilen; jede einzelne dieser
Gruppen drückt gewisse zusammengehörige Grundtatsachen unserer Anschauung
aus. Wir benennen diese Gruppen von Axiomen in folgender Weise:
I 1-8. Axiome der Verknüpfung,
II 1-4. Axiome der Anordnung,
III 1-5. Axiome der Kongruenz,
IV Axiom der Parallelen,
V 1-2. Axiom der Stetigkeit.
I. Axiome der Verknüpfung. 1. Zu zwei Punkten A, B gibt es stets eine Gerade
a , die mit jedem der beiden Punkte A, B zusammengehört. 2. Zu zwei Punkten
A, B gibt es nicht mehr als eine Gerade, die mit jedem der beiden Punkte A, B
zusammengehört. 3. Auf einer Geraden gibt es stets wenigstens zwei Punkte. Es
gibt wenigstens drei Punkte, die nicht auf einer Geraden liegen. 4. Zu irgend drei
nicht auf ein und derselben Geraden liegenden Punkten A, B, C gibt es stets eine
Ebene α, die mit jedem der drei Punkte A, B, C zusammengehört. Zu jeder Ebene
gibt es stets einen mit ihr zusammengehörigen Punkt. 5. Zu irgend drei nicht auf ein
und derselben Geraden liegenden Punkten A, B, C gibt es nicht mehr als eine Ebene,
die mit jedem der drei Punkte A, B, C zusammengehört. 6. Wenn zwei Punkte einer
Geraden a in einer Ebene α liegen, so liegt jeder Punkt von a in der Ebene α. 7.
Wenn zwei Ebenen einen Punkt gemein haben, so haben sie wenigstens noch einen
weiteren Punkt gemein. 8. Es gibt wenigstens vier nicht in einer Ebene gelegene
Punkte.
II. Axiome der Anordnung. 1. Wenn ein Punkt B zwischen einem Punkt A
und einem Punkt C liegt, so sind A, B, C drei verschiedene Punkte einer Geraden,
und B liegt dann auch zwischen C und A. 2. Zu zwei Punkten A und C gibt es
stets wenigstens einen Punkt B auf der Geraden AC, so daß C zwischen A und
B liegt. 3. Unter irgend drei Punkten einer Geraden gibt es nicht mehr als einen,
der zwischen den beiden anderen liegt. 4. Es seien A, B, C drei nicht in gerader
Linie gelegene Punkte und a eine Gerade in der Ebene ABC, die keinen der Punkte
A, B, C trifft: wenn dann die Gerade a durch einen Punkt der Strecke AB geht, so
geht sie gewiß auch entweder durch einen Punkt der Strecke AC oder durch einen
Punkt der Strecke BC.
III. Axiome der Kongruenz. 1. Wenn A, B zwei Punkte auf einer Geraden a
und ferner A0 ein Punkt auf derselben oder einer anderen Geraden a0 ist, so kann
man auf einer gegebenen Seite der Geraden a0 von A0 stets einen Punkt B 0 finden,
so daß die Strecke AB der Strecke A0 B 0 kongruent ist, in Zeichen: AB ≡ A0 B 0 . 2.
3
Wenn eine Strecke A0 B 0 und eine Strecke A00 B 00 derselben Strecke AB kongruent
sind, so ist auch die Strecke A0 B 0 der Strecke A00 B 00 kongruent. 3. Es seien AB und
BC zwei Strecken ohne gemeinsame Punkte auf der Geraden a und ferner A0 B 0
und B 0 C 0 zwei Strecken auf derselben oder einer anderen Geraden a0 ebenfalls ohne
gemeinsame Punkte; wenn dann AB ≡ A0 B 0 und BC ≡ B 0 C 0 ist, so ist auch stets
AC ≡ A0 C 0 . 4. Es sei ein Winkel 6 (h, k) in einer Ebene α und eine Gerade a0 in
einer Ebene α0 sowie eine bestimmte Seite von a0 in α0 gegeben. Es bedeute h0 einen
Halbstrahl der Geraden a0 , der vom Punkte O0 ausgeht: dann gibt es in der Ebene
α0 einen und nur einen Halbstrahl k 0 , so daß der Winkel 6 (h, k) kongruent dem
Winkel 6 (h0 , k 0 ) ist und zugleich alle inneren Punkte des Winkels 6 (h0 , k 0 ) auf der
gegebenen Seite von a0 liegen, in Zeichen: 6 (h, k) ≡ 6 (hl, k 0 ). Jeder Winkel ist sich
selbst kongruent. 5. Wenn für zwei Dreiecke ABC und A0 B 0 C 0 die Kongruenzen
AB ≡ A0 B 0 , AC ≡ A0 C 0 , 6 BAC ≡ 6 B 0 A0 C 0 gelten, so ist auch stets die Kongruenz
6 ABC ≡ 6 A0 B 0 C 0 erfüllt.
IV. Axiom der Parallelen. Es sei a eine beliebige Gerade und A ein Punkt
außerhalb a: dann gibt es in der durch a und A bestimmten Ebene höchstens (bzw.
genau) eine Gerade, die durch A läuft und a nicht schneidet.
V. Axiome der Stetigkeit. 1. (Archimedisches Axiom.) Sind AB und CD irgendwelche Strecken, so gibt es eine Anzahl n derart, daß das n-malige HintereinanderAbtragen der Strecke CD von A aus auf den durch B gehenden Halbstrahl über
den Punkt B hinausführt.
2. (Vollständigkeitsaxiom.) Die Punkte der Geraden bilden ein System, welches bei
Aufrechterhaltung der Axiome I1-2, II, III, VI keiner Erweiterung mehr fähig ist.
4
Empirische Geometrie für den Mathematikunterricht in der Sekundarstufe I
Der Geometrieunterricht in der Sekundarstufe I befindet sich zur Zeit in einem
starken Umbruch. Einerseits erkannte man nach mehr als fünfzehn Jahren Verzicht auf Geometrie zugunsten von neuen strukturmathematischen Theorieteilen
das Defizit, das auf Grund des anerkannten Bildungswerts der Geometrie entstand,
und andererseits bieten sich durch die neuen interaktiven Geometrieprogramme auf
preisgünstigen Computern völlig neue Lernmöglichkeiten, die vor allem Kreativität
und Problemlösefähigkeiten fördern. Auf die dadurch stark veränderte Unterrichtssituation müssen auch die Studierenden des Lehramts Mathematik angemessen vorbereitet werden. Die dafür notwendige Entwicklung einer geeigneten Hintergrundtheorie wird glücklicherweise durch die Habilitationsschrift des inzwischen anerkannten
Geometriedidaktikers Horst Struve vorbereitet und erleichtert. Eine überarbeitete Fassung ist als Buch mit dem Titel “Grundlagen einer Geometriedidaktik” [11]
erschienen.
In der Einleitung konstatiert er, dass es verschiedene Auffassungen vom ontologischen Status der Objekte der Mathematik gibt, nämlich die formalistische, die
intuitionistische, die konstruktivistische und die platonische Auffassung. Es ist bekannt, dass eine große Mehrzahl der LehrerInnen den platonistischen Standpunkt
vertritt, der eine “Präexistenz” der mathematischen Objekte und Ergebnisse annimmt. Nach Struves Ansicht bleibt damit eine wesentliche Aufgabe: Es handelt
sich um das Problem der “ontologischen Rechtfertigung” aus Schülersicht und nicht
aus Lehrersicht.
Die Gliederung seines Buches entspricht im wesentlichen den folgenden drei Schritten seines Vorgehens:
4
i) Analyse des Geometrieunterrichts an Hand des Schulbuchs GAMMA;
ii) Untersuchung der Geschichte der drei Begriffe “Gerade”, “Ebene” und “geometrische Abbildung”;
iii) Formalisierung der “empirischen Geometrie”.
Bei der Analyse der GAMMA-Lerneinheit “Falten und Zeichnen” entwickelt Struve
die folgenden grundlegenden Gedanken. In dieser Altersstufe werden Gegenstände
(Begriffe) der Geometrie “operational” eingeführt, das heißt durch Angabe von Konstruktionsvorschriften. Insbesondere wird also durch Handlungen ein unmittelbarer
Bezug zur Realität aufrecht erhalten. In diesem Zusammenhang setzt er sich mit
dem Problem der “unendlich” ausgedehnten Objekte (Strahl, Gerade, Ebene) auseinander, die den derzeit gültigen physikalischen Theorien zufolge in der Realität
gar nicht existieren.
Für einen bewussten Abstraktionsschritt fehlen in dieser Altersstufe noch die geistigen Voraussetzungen und Erfahrungen. Ein erster Schritt, den wir in Kapitel 5 (“Genese von Sätzen der empirischen Geometrie”) versuchen, besteht in der Einführung
von Beschreibungsbegriffen, die dann Abkürzungen von langen und umständlichen
Sprechweisen sind. Eine “Halbgerade” etwa beschreibt die Möglichkeit, eine Strecke
über einen Endpunkt hinaus beliebig (nach Bedarf) zu verlängern.
An Hand des Schulbuchs analysiert Struve auch die Beweisproblematik in dieser
Altersstufe. Auf Grund seiner Tätigkeiten lernt der Schüler zwar Sätze kennen, der
Gültigkeitsgrund dieser Sätze ist aber lediglich die Erfahrung, die der Schüler gemacht hat. (Bei uns bilden solche “evidenten” Sätze den “Geogarten”, den wir in Kapitel 5 einführen.) Am Beispiel des Winkelsummensatzes arbeitet Struve zwei Funktionen des Beweises heraus. Sie dienen entweder der Wissensbegründung (nämlich
dem Nachweis von Gültigkeit) oder zum Systematisieren von Wissen, indem sie Zusammenhänge zu anderen Aussagen aufzeigen. Hier kommt für die Schüler zunächst
nur die zweite Sichtweise zur Geltung. Die anfangs gestellte Frage nach der “ontologischen Rechtfertigung” der Geometrie beantwortet Struve in der Zusammenfassung
der Analyse folgendermaßen: “Geometrie - so wie sie der Schüler erfährt - dient dazu, gewisse Phänomene der Realität zu beschreiben und zu erklären ...” Da eine
Theorie, die Phänomene der Realität beschreibt und erklärt, üblicherweise eine empirische Theorie genannt wird, bezeichnet Struve die Geometrie der Sekundarstufe
I als “empirische Geometrie”.
Als wesentliche Charakteristika empirischer Theorien führt er die “intendierten”
Anwendungen, den ontologischen Status der Begriffe und die Rolle von Sätzen und
Beweisen an. Unter dem zweiten Punkt beschreibt er eine wichtige Klasseneinteilung der Begriffe einer empirischen Theorie. In die erste Klasse fallen Begriffe, die
sich “unmittelbar” auf die Realität beziehen. Hier sind noch zwei Typen zu unterscheiden. In einer “operationalen” Definition wird ein Begriff durch Angabe einer
Konstruktionsvorschrift eingeführt (z. B. Strecke und Kreis), während “ostensive”
Begriffe durch Aufzeigen von Beispielen und Gegenbeispielen definiert werden (z. B.
Parallelität oder - im täglichen Leben - Farben). Zu einer zweiten Klasse von Begriffen einer empirischen Theorie gehören solche, deren Bedeutung von der Theorie
abhängt. Zur Überprüfung einer Hypothese, in der ein solcher Begriff vorkommt,
muss man die Theorie bereits voraussetzen. In der empirischen Geometrie sind Halbgerade, Gerade, Ebene und geometrische Abbildung solche Begriffe. Struve gelingt
es durch diese Unterscheidung, die Schwierigkeiten zu erklären, die viele Schüler mit
solchen Begriffen haben.
Das Buch “Geometrie in der Sekundarstufe” von Gerhard Holland [5] stellt eine gute Grundlage für den Aufbau dieser Vorlesung dar, die im Prinzip denselben Titel
5
- mit Sekundarstufe I anstelle von Sekundarstufe bei Holland - trägt. Es handelt
sich um eine sehr gründliche Zusammenstellung der verschiedensten Aspekte des
Geometrieunterrichts in der Sekundarstufe I. Unser Ziel ist es darüber hinaus, unter Berücksichtigung der aktuellen Entwicklung konkrete curriculare Sequenzen zu
konstruieren.
Im ersten Satz der Einleitung beschreibt Holland die vielfältigen Aufgaben, die
MathematiklehrerInnen wahrzunehmen haben:
Bei der Unterrichtsvorbereitung und im Unterrichtsgeschehen werden vom Lehrer
laufend Entscheidungen abverlangt, die er nur dann rational begründbar fällen kann,
wenn ihm die fachdidaktische Ausbildung geeignete Kriterien und eine gründliche
Kompetenz zu ihrer Handhabung vermittelt hat.
Die Kapiteleinteilung wurde von Holland so gestaltet, dass zur Verbesserung der
folgenden acht Kompetenzen Hilfen geboten werden: Inhaltsanalyse, Sachanalyse,
Lehrstoffanalyse, Prozesszielanalyse, Lehrzielauswahl, Lehrstoffsequenzierung, methodische Gestaltung von Lernsequenzen und Ausarbeitung von Lernsequenzen zum
Problemlösen.
Das erste Kapitel hat sechs Unterkapitel. Der erste Teil des Titels von 1.1 “Inhaltsziele und Prozessziele” ist weitgehend unproblematisch. Zu dem zweiten Teil schreibt
Holland zunächst: Prozessziele beziehen sich auf mathematische Aktivitäten, wie
z. B. Beweisen, Konstruieren, Mathematisieren, und betreffen die Fähigkeiten zu
derartigen Aktivitäten. Ausführlich beschreibt er dann sieben Kategorien von Prozesszielen: Fähigkeiten zum Entdecken mathematischer Zusammenhänge, zum Formalisieren, zum Definieren, zum Beweisen, zum Axiomatisieren, zum Problemlösen
und zum Mathematisieren.
Das Thema “verschiedene Aspekte von Geometrie” des Unterkapitels 1.2 ist auch für
unseren Aufbau wegweisend. Genannt werden dort: Lehre vom Anschauungsraum,
Beispiel einer deduktiven Theorie, Übungsfeld für Problemlösen und Vorrat mathematischer Strukturen. Die übrigen Unterkapitel behandeln Inhalte des Geometrieunterrichts (nach Altersstufen und Themenbereichen gegliedert), Orientierung des
Geometriecurriculums, Lehrstoffanalyse und Lehrzielauswahl sowie Strukturierung
des Lehrstoffs.
5
Genese von Sätzen der ebenen empirischen Geometrie
Im Anschluss an H. Struve entwickeln wir ein System von Sätzen, die ausgehend von
Erfahrungen jeweils zusammen mit Grundbegriffen und mit Beschreibungsbegriffen
(in Anführungsstrichen) durch folgende Prozessschritte gewonnen werden:
i) Festlegung eines (neuen) Grundbegriffs,
ii) Sammlung von Handlungsergebnissen bzw. von Messbefunden,
iii) Bildung von Hypothesen.
Das Ergebnis, das hier noch nicht vollständig dargestellt werden kann, nennen wir
“Geogarten”. Damit soll auf die Wachstumsvorgänge hingewiesen werden, die sich
wesentlich von fertigen Produkten (z. B. Axiomensystemen) unterscheiden. Die im
Hinblick auf Intuition und Plausibilität (für die Lernenden) zu wählende Reihenfolge
der grundlegenden Sätze stellt noch ein schwieriges didaktisches Problem dar. Die
Zusammenstellung dieser Sätze als “Fundus” im nächsten Abschnitt berücksichtigt
nicht die Reihenfolge der Herleitung, sondern erfolgt aus Zweckmäßigkeitsgründen
in Satzgruppen mit suggestiven Namen.
6
1. Punkt
Es sind keine Messungen möglich. Hypothese: Punkte haben keine messbare Eigenschaft. Die Vorstellung eines Punktes entsteht durch Beobachtung immer kleinerer
Gegenstände.
2. Strecke
Handlungen: Falten von Papier (kritisch: Papier-“Ebene”), visieren, Lot herstellen,
Seil spannen.
Streckensatz: Jede Strecke hat zwei “Endpunkte”. Zu je zwei verschiedenen Punkten gehört genau eine “Verbindungsstrecke”, deren Endpunkte die Punkte sind. Für
jede Strecke und jeden Punkt lässt sich entscheiden, ob der Punkt “auf der Strecke
liegt”, oder nicht und ob er Endpunkt ist oder nicht. Jede Strecke wird durch jeden
auf ihr liegenden Punkt, der kein Endpunkt ist, in zwei “Teilstrecken” zerlegt. Bei
Bedarf kann jede Strecke über ihre Endpunkte hinaus “verlängert” werden, so dass
eine Strecke entsteht, die die “Ausgangsstrecke” als Teilstrecke enthält.
“Strahl” (“Halbgerade”) und “Gerade” sind Beschreibungsbegriffe für geeignete
Strecken, die in der jeweiligen Situation durch Verlängerung einer Strecke über
einen Endpunkt bzw. über beide Endpunkte hinaus entstehen.
3. Längenvergleich von Strecken
Handlungen: “Bewegen” eines “Maßstabs”, “Abtragen” einer Strecke auf einem
Strahl.
Längenvergleichssatz: Jedem Streckenpaar kommt genau eine der folgenden drei
Eigenschaften zu: Beide Strecken sind “gleich lang”, oder die erste Strecke ist
“kürzer” als die zweite, oder die erste ist “länger” als die zweite.
4. Dreieck und Winkel
Drei Punkte, die nicht auf einer ihrer Verbindungsstrecken liegen, heißen zusammen
mit den drei Verbindungsstrecken “Dreieck”. Die Punkte werden “Eckpunkte” und
die Verbindungsstrecken “Seiten” des Dreiecks genannt.
Zwei Strahlen, die von einem Punkt ausgehen, bilden einen “Winkel”. Zwei in einem
Punkt beginnende Strahlen ergeben einen “gestreckten Winkel”, wenn jeder der
Strahlen auf der Verlängerung des anderen “liegt”. Die Strahlen, die einen Winkel
bilden, heißen “Schenkel” des Winkels, der gemeinsame Endpunkt wird “Scheitel”
oder “Scheitelpunkt” des Winkels genannt.
Handlungen: “Bewegen” von Dreiecken, “Abtragen” und “Vergleichen” von Winkeln
mit Hilfe von “gleichschenkligen” Dreiecken.
Winkelvergleichssatz: Jedem Winkelpaar kommt genau eine der folgenden drei
Eigenschaften zu: Beide Winkel sind “gleich groß”, oder der erste Winkel ist “kleiner” als der zweite, oder der erste ist “größer” als der zweite.
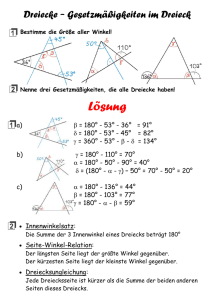
Basiswinkelsatz: In einem Dreieck sind zwei Seiten genau dann gleich lang, wenn
die “gegenüberliegenden” Winkel gleich groß sind.
Achtung: Sätze mit “... genau dann, wenn ...” entstehen durch Zusammenfassen von
zwei “... wenn ... , dann ...”-Sätzen.
Dreiecksseitensatz: In einem Dreieck ist bei jedem Seitenpaar die erste Seite
genau dann länger als die andere, wenn der gegenüberliegende Winkel der ersten
Seite größer ist als der gegenüberliegende der zweiten.
Zwei Dreiecke heißen “kongruent”, wenn es zu jeder Seite des einen Dreiecks eine
gleich lange Seite des anderen gibt und wenn die Winkel, die den entsprechenden
7
Seiten gegenüberliegen, gleich groß sind. Zwei Dreiecke heißen “ähnlich”, wenn es
zu jedem Winkel des einen Dreiecks einen gleich großen Winkel des anderen gibt.
Kongruenzsatz: Zwei Dreiecke sind kongruent, wenn eine der folgenden Übereinstimmungen vorliegt:
i) Die Länge aller drei Seiten (SSS).
ii) Die Länge von zwei Seiten und die Größe des von diesen “eingeschlossenen” Winkel (SWS).
iii) Die Länge von zwei Seiten und die Größe des Winkels, der der längeren Seite
gegenüberliegt (WsS).
iv) Die Länge einer Seite und entweder die Größe der beiden “anliegenden” Winkel (WSW) oder die Größe des gegenüberliegenden und eines anliegenden Winkels
(SWW).
Zwei Geraden “schneiden” sich, wenn es genau einen Punkt gibt, der auf beiden
Geraden liegt. Die vier von diesem Punkt ausgehenden Strahlen auf den Geraden
bilden vier Winkel. Je zwei der Winkel, die einen Strahl gemeinsam haben heißen
“Nebenwinkel”, die übrigen Paare von Winkeln werden “Scheitelwinkel” genannt.
Winkelsatz: Scheitelwinkel sind gleich groß. Die beiden Nebenwinkel, die durch
Verlängerung der beiden Schenkel eines Winkels entstehen, sind gleich groß.
Ein Winkel heißt “rechter Winkel”, wenn er genauso groß ist, wie einer der beiden
Nebenwinkel, die durch Verlängerung eines Schenkels entstehen. Die Größe eines
rechten Winkels wird mit R bezeichnet, die Größe eines gestreckten Winkels mit
2R. Zwei sich schneidende Geraden heißen “senkrecht”, wenn die von ihrem Schnittpunkt ausgehenden und nicht auf derselben Geraden liegenden Strahlen einen rechten Winkel bilden.
Zwei Strecken, Halbgeraden oder Geraden heißen “parallel”, wenn es eine Gerade
gibt, die auf jeder der beiden “Verlängerungsgeraden” senkrecht steht.
6
Fundus der Elementargeometrie
1. Basiswinkelsatz: In einem gleichschenkligen Dreieck sind die “Basiswinkel”
gleich groß. Sind in einem Dreieck zwei Winkel gleich groß, so sind die “gegenüberliegenden” Seiten gleich lang.
2. Dreiecksseitensatz: In einem Dreieck ist bei jedem Seitenpaar die erste Seite
genau dann länger als die andere, wenn der gegenüberliegende Winkel der ersten
Seite größer ist als der gegenüberliegende Winkel der zweiten.
3. Kongruenzsatz: Zwei Dreiecke sind kongruent, wenn eine der folgenden Übereinstimmungen vorliegt:
i) Die “Länge” aller drei Seiten (SSS).
ii) Die Länge von zwei Seiten und die “Größe” des von diesen eingeschlossenen Winkels (SWS).
iii) Die Länge von zwei Seiten und die Größe des Winkels, der der längeren Seite
gegenüberliegt (WsS).
iv) Die Länge einer Seite und entweder die Größe der beiden “anliegenden” Winkel (WSW) oder die Größe des gegenüberliegenden und eines anliegenden Winkels
(SWW).
4. Winkelsatz: Scheitelwinkel sind gleich groß. Die beiden Nebenwinkel, die durch
Verlängerung der beiden Schenkel eines Winkels entstehen, sind gleich groß.
8
5. Parallelensatz: Je zwei Stufen- oder Wechselwinkel an geschnittenen Parallelen
sind paarweise gleich; entgegengesetzte Winkel ergänzen sich zu 2R.
Werden zwei Geraden von einer dritten Geraden geschnitten und sind je zwei Stufenbzw. Wechselwinkel einander gleich oder ergänzen sich je zwei entgegengesetzte
Winkel zu 2R, so sind die geschnittenen Geraden parallel.
6. Seitensummensatz: Die “Streckensumme” zweier Seiten eines Dreiecks ist
länger als die dritte Seite.
7. Innenwinkelsatz: Die “Winkelsumme” der “Innenwinkel” eines Dreiecks beträgt
2R.
8. Außenwinkelsatz: Jeder “Außenwinkel” eines Dreiecks ist so groß wie die Winkelsumme der ihm nicht benachbarten Innenwinkel.
9. Drachensatz: Die “Verbindungslinie” der “Spitzen” zweier gleichschenkliger
Dreiecke mit gemeinsamer “Basis” steht senkrecht auf der Basis, halbiert sie und
die Winkel an den Spitzen.
10. Gleichschenkelsatz: Die Verbindungslinie der Spitze eines gleichschenkligen
Dreiecks mit der Mitte der Basis halbiert den Winkel an der Spitze und steht senkrecht auf der Basis.
Die “Mittelsenkrechte” der Basis eines gleichschenkligen Dreiecks geht durch die
Spitze und halbiert den Winkel an der Spitze.
Die “Halbierungslinie” des Winkels an der Spitze eines gleichschenkligen Dreiecks
halbiert die Basis und steht senkrecht auf ihr.
Das “Lot” von der Spitze eines gleichschenkligen Dreiecks auf die Basis halbiert
diese und den Winkel an der Spitze.
11. Mittelsenkrechtensatz: Jeder Punkt der Mittelsenkrechten einer Strecke hat
gleichen “Abstand” von den Endpunkten der Strecke.
Alle Punkte, die von den Endpunkten einer Strecke gleichen Abstand haben, liegen
auf der Mittelsenkrechten der Strecke.
12. Winkelhalbierendensatz: Jeder Punkt der “Winkelhalbierenden” eines Winkels hat gleichen Abstand von den Schenkeln.
Alle Punkte, die gleichen Abstand von den Schenkeln eines Winkels haben, liegen
auf der Winkelhalbierenden des Winkels.
13. Parallelogrammsatz: Das “Parallelogramm” wird durch jede seiner “Diagonalen” in zwei kongruente Dreiecke zerlegt, und die Diagonalen halbieren sich gegenseitig.
Im Parallelogramm sind die “Gegenseiten” und die “Gegenwinkel” gleich; die einer
Seite anliegenden Winkel betragen 2R.
Ein “Viereck” ist ein Parallelogramm, wenn die Gegenseiten oder die gegenüberliegenden Winkel gleich sind oder wenn sich die Diagonalen gegenseitig halbieren oder
wenn ein Paar Gegenseiten gleich und parallel sind.
Ein Parallelogramm ist genau dann ein “Rhombus”, wenn die Diagonalen senkrecht
aufeinander stehen oder wenn die Diagonalen die Winkel halbieren. Ein Parallelogramm ist genau dann ein “Rechteck”, wenn die Diagonalen gleich lang sind.
Ein Parallelogramm ist genau dann ein “Quadrat”, wenn die Diagonalen senkrecht
aufeinander stehen und gleich lang sind.
14. Trapezsatz: Im “Trapez” betragen die einem Schenkel anliegenden Winkel zusammen 2R.
Die “Grundlinienparallele” durch die Mitte eines Schenkels eines Trapezes halbiert
9
den anderen Schenkel.
Die Verbindungslinie der Mitten der Schenkel eines Trapezes läuft den Grundlinien
parallel.
Die “Mittellinie” einen Trapezes ist gleich der halben Summe der beiden Grundlinien.
15. Seitenmittensatz: Zieht man durch die Mitte einer Dreiecksseite die Parallele
zu einer zweiten Seite, so halbiert diese die dritte Seite.
Die Verbindungslinie der Mitten zweier Dreiecksseiten läuft der dritten Seite parallel
und ist halb so lang wie diese.
16. Seitenhalbierendensatz: Der Schnittpunkt von zwei “Seitenhalbierenden” eines Dreiecks teilt jede der beiden Seitenhalbierenden im Verhältnis 2:1.
Die drei Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt (dem
“Schwerpunkt”).
17. Sehnensatz: Das vom “Mittelpunkt” eines “Kreises” auf eine “Sehne” gefällte
Lot halbiert den “Mittelpunktswinkel”, die Sehne und den “Bogen”.
Gleiche Sehnen haben gleichen Abstand vom Mittelpunkt.
Zu gleichen Sehnen gehören gleiche Mittelpunktswinkel und gleiche Bogen.
Der Mittelpunkt eines Kreises, der eine Strecke als Sehne hat, liegt auf der Mittelsenkrechten der gegebenen Strecke.
Haben zwei Kreise eine Sehne gemeinsam, so steht diese auf der Verbindungsstrecke
der Mittelpunkte senkrecht.
18. Umkreissatz: Die Mittelsenkrechten der Seiten eines Dreiecks schneiden sich
in einem Punkte, der Mittelpunkt des “Umkreises” ist.
19. Höhenschnittsatz: Die “Höhen” eines Dreiecks schneiden sich in einem Punkte.
20. Rechtwinkelsatz (Satz von Thales): Der Umfangswinkel im “Halbkreis” ist
ein Rechter. Die Spitzen aller “rechtwinkligen Dreiecke” über einer gemeinsamen
“Hypotenuse” liegen auf einem Halbkreis.
21. Umfangswinkelsatz: Alle “Umfangswinkel” über demselben Bogen sind gleich.
Sie sind halb so groß wie der Mittelpunktswinkel über demselben Bogen.
22. Tangentensatz: Die Senkrechte im Endpunkt eines Radius ist “Tangente” des
Kreises. Der “Sehnentangentenwinkel” ist halb so groß wie der Mittelpunktswinkel,
der mit ihm über demselben Bogen steht.
Werden von einem Punkt P außerhalb des Kreises die beiden Tangenten an den
Kreis gezogen, so sind die Abschnitte bis zu den Berührungspunkten einander gleich.
23. Inkreissatz: Die Winkelhalbierenden eines Dreiecks schneiden sich in einem
Punkt, dem Mittelpunkt des “Inkreises”.
Ein Punkt W auf der Winkelhalbierenden h des Winkels ϕ ∈ {α, β, γ} ist genau
dann Inkreismittelpunkt, wenn der Winkel zwischen den Verbindungsstrecken von
W mit den beiden nicht auf h liegenden Eckpunkten 90◦ + ϕ/2 beträgt.
24. Parallelogrammflächensatz: Parallelogramme mit gleichen Grundlinien und
Höhen sind “flächengleich”. Der “Flächeninhalt” eines Dreiecks ist halb so groß wie
der eines Parallelogramms mit gleicher Grundlinie und Höhe.
Ein Trapez ist flächengleich mit einem Parallelogramm, das dieselbe Höhe hat und
dessen Grundlinie so lang ist wie die Mittellinie des Trapezes.
10
25. Kathetensatz (Erster Satz von Euklid): Im rechtwinkligen Dreieck ist das
Quadrat über einer “Kathete” flächengleich dem Rechteck aus der Hypotenuse und
der “Projektion” der Kathete auf die Hypotenuse.
26. Quadratsummensatz (Satz von Pythagoras): Im rechtwinkligen Dreieck
ist das Quadrat über der Hypotenuse “flächengleich” mit der Summe der Quadrate
über den Katheten.
27. Höhensatz (Zweiter Satz von Euklid): Im rechtwinkligen Dreieck ist das
Quadrat über der Höhe flächengleich mit dem Rechteck aus den beiden Hypotenusenabschnitten.
28. Strahlensatz: Werden zwei Strahlen von zwei Parallelen geschnitten, so verhalten sich die Abschnitte des einen Strahls wie die entsprechenden des andern.
Werden zwei Strahlen von zwei Geraden so geschnitten, dass die Abschnitte des
einen Strahls sich wie die entsprechenden des anderen verhalten, so sind die Geraden parallel.
Werden zwei Strahlen von zwei Parallelen geschnitten, so verhalten sich die Abschnitte auf den Parallelen wie die Abschnitte vom Strahlenschnittpunkt bis zu den
Parallelen.
Werden zwei Parallelen durch drei Strahlen geschnitten, so verhalten sich die Abschnitte der einen Parallelen wie die entsprechenden der anderen.
29. Ähnlichkeitssatz: Zwei Dreiecke sind ähnlich, wenn eine der folgenden Übereinstimmungen vorliegt:
i) Die Größe von zwei Winkeln.
ii) Das Verhältnis von zwei Seiten und der von diesen eingeschlossene Winkel.
iii) Zwei Seitenverhältnisse.
iv) Das Verhältnis von zwei Seiten und der Winkel, der der größeren von beiden
gegenüberliegt.
30. Dreiecksvergleichssatz: In ähnlichen Dreiecken stehen alle entsprechenden
Stücke (Höhen, Seitenhalbierende, Winkelhalbierende, “Radien” des In- und Umkreises, der “Ankreise”) in demselben Verhältnis wie entsprechende Seiten.
31. Seitenteilungssatz: Die Winkelhalbierende eines Dreieckswinkels bzw. die seines Außenwinkels teilt die gegenüberliegende Seite innen bzw. außen im Verhältnis
der den Winkel einschließenden Seiten.
Die Winkelhalbierende eines Innenwinkels und die seines Außenwinkels teilen die
gegenüberliegende Seite harmonisch im Verhältnis der Seiten.
32. Seitenverhältnissatz (Satz des Apollonius): Die Spitzen von Dreiecken,
von denen eine Seite und das Verhältnis der beiden anderen gegeben sind, liegen
auf dem Halbkreis über der Verbindungslinie der Teilpunkte, die die gegebene Seite
im Verhältnis der beiden anderen harmonisch teilen.
33. Sehnenabschnittssatz: Werden durch einen Punkt innerhalb eines Kreises
zwei Sehnen gezogen, so ist das Rechteck aus den Abschnitten der einen flächengleich
mit dem Rechteck aus den Abschnitten der anderen Sehne.
34. Sekantensatz: Zieht man von einem Punkte außerhalb eines Kreises zwei Sekanten, so ist das Rechteck aus der einen ganzen Sekante und ihrem äußeren Abschnitt flächengleich mit dem Rechteck aus den entsprechenden Strecken der anderen.
35. Sekantentangentensatz: Zieht man von einem Punkte außerhalb eines Kreises
eine Sekante und eine Tangente, so ist das Rechteck aus der ganzen Sekante und
ihrem äußeren Abschnitt flächengleich mit dem Quadrat über der Tangente.
11
36. Goldschnittsatz: Ist der Durchmesser eines Kreises Kathete eines gleichschenklig-rechtwinkligen Dreiecks, so wird die vom Endpunkt der zweiten Kathete gezogene “Zentrale” durch den Kreis nach dem “goldenen Schnitt” geteilt. (Eine Zentrale
verläuft von einem Punkt außerhalb eines Kreises durch den Mittelpunkt bis zum
Endpunkt des zugehörigen Durchmessers.)
Trägt man den kleineren Abschnitt einer nach dem goldenen Schnitt geteilten
Strecke auf dem größeren Abschnitt ab, so wird auch dieser nach dem goldenen
Schnitt geteilt.
37. Drehstrecksatz: Zwei Dreiecke ABC und A0 B 0 C 0 , für die AA0 , BB 0 und CC 0
nicht auf Parallelen liegen, sind genau dann ähnlich mit 6 BAC = 6 B 0 A0 C 0 und
6 CBA = 6 C 0 B 0 A0 , wenn es einen Punkt O mit 6 AOA0 = 6 BOB 0 = 6 COC 0 und
|OA|/|OA0 | = |OB|/|OB 0 | = |OC|/|OC 0 | gibt.
Die folgenden beiden bekannten Sätze sind Beispiele von nicht zum Fundus gehörenden Sätzen, weil sie nur wenige Anwendungen besitzen. Sie lassen sich aber mit
Sätzen aus dem Fundus herleiten.
Vierpunktesatz (Satz von Euler): Der Höhenschnittpunkt H, der Schwerpunkt
S und der Umkreismittelpunkt M eines Dreiecks sowie der Umkreismittelpunkt
N des “Mittendreiecks” liegen auf einer Geraden (“Eulersche Gerade”). Dabei ist
|SH| = 2|SM | = 4|SN |.
Neunpunktesatz (Satz von Feuerbach): Die drei “Höhenfußpunkte” und die
Mittelpunkte der Seiten und der oberen “Höhenabschnitte” liegen auf dem Umkreis
des Mittendreiecks (“Feuerbachscher Neunpunktekreis”).
7
Pólyas Heuristik-Checkliste (HCl)
(aus: G. Pólya, Schule des Denkens, Francke Verlag Bern e.a. 1967; Innendeckel)
Wie sucht man die Lösung?
Erstens
Du mußt die Aufgabe verstehen.
Zweitens
Suche den Zusammenhang zwischen den Daten und der Unbekannten.
Du mußt vielleicht Hilfsaufgaben betrachten, wenn ein unmittelbarer Zusammenhang nicht gefunden werden kann.
Du mußt schließlich den Plan der Lösung erhalten.
Drittens
Führe Deinen Plan aus.
Viertens
Prüfe die erhaltene Lösung.
(1) Verstehen der Aufgabe
• Was ist unbekannt? Was ist gegeben? Wie lautet die Bedingung?
• Ist es möglich, die Bedingung zu befriedigen? Ist die Bedingung ausreichend, um
die Unbekannte zu bestimmen? Oder ist sie unzureichend? Oder überbestimmt?
Oder kontradiktorisch?
• Zeichne eine Figur! Führe eine passende Bezeichnung ein!
• Trenne die verschiedenen Teile der Bedingung! Kannst Du sie hinschreiben?
12
(2) Ausdenken eines Planes
• Hast Du die Aufgabe schon früher gesehen? Oder hast Du dieselbe Aufgabe in
einer wenig verschiedenen Form gesehen?
• Kennst Du eine verwandte Aufgabe? Kennst Du einen Lehrsatz, der förderlich
sein könnte?
• Betrachte die Unbekannte! Und versuche, Dich auf eine Dir bekannte Aufgabe zu
besinnen, die dieselbe oder eine ähnliche Unbekannte hat.
• Hier ist eine Aufgabe, die der Deinen verwandt und schon gelöst ist. Kannst Du
sie gebrauchen? Kannst Du ihr Resultat verwenden? Kannst Du ihre Methode verwenden? Würdest Du irgend ein Hilfselement einführen, damit Du sie verwenden
kannst?
• Kannst Du die Aufgabe anders ausdrücken? Kannst Du sie auf noch verschiedene
Weise ausdrücken? Geh auf die Definition zurück!
• Wenn Du die vorliegende Aufgabe nicht lösen kannst, so versuche, zuerst eine
verwandte Aufgabe zu lösen. Kannst Du Dir eine zugänglichere verwandte Aufgabe
denken? Eine allgemeinere Aufgabe? Eine speziellere Aufgabe? Eine analoge Aufgabe? Kannst Du einen Teil der Aufgabe lösen? Behalte nur einen Teil der Bedingung
bei und lasse den anderen fort; wie weit ist die Unbekannte dann bestimmt, wie kann
ich sie verändern? Kannst Du etwas Förderliches aus den Daten ableiten? Kannst
Du Dir andere Daten denken, die geeignet sind, die Unbekannte zu bestimmen?
Kannst Du die Unbekannte ändern oder die Daten oder, wenn nötig, beide, so dass
die neue Unbekannte und die neuen Daten einander näher sind?
• Hast Du alle Daten benutzt? Hast Du die ganze Bedingung benutzt? Hast Du alle
wesentlichen Begriffe in Rechnung gezogen, die in der Aufgabe enthalten sind?
(3) Ausführen des Planes
• Wenn Du Deinen Plan der Lösung durchführst, so kontrolliere jeden Schritt.
Kannst Du deutlich sehen, dass der Schritt richtig ist? Kannst Du beweisen, dass
er richtig ist?
(4) Rückschau
• Kannst Du das Resultat kontrollieren? Kannst Du den Beweis kontrollieren? •
Kannst Du das Resultat auf verschiedene Weise ableiten? Kannst Du es auf den
ersten Blick sehen?
• Kannst Du das Resultat oder die Methode für irgend eine andere Aufgabe gebrauchen?
8
Übungen zur Vorlesung “Geometrie”
(WS 1999/2000)
Aufgabe 1:
a) Stellen Sie Sätze bzw. Axiome zusammen, mit denen der Basiswinkelsatz bewiesen werden könnte.
b) Geben Sie (mindestens) vier Sätze aus der Liste an, in deren Beweis der Basiswinkelsatz auftreten kann.
Aufgabe 2:
In der Ebene seien drei beliebige (nicht zusammenfallende) Parallelen gegeben. Beschreiben und begründen Sie ein Konstruktionsverfahren für ein gleichseitiges Dreieck, dessen Ecken auf je einer der Parallelen liegen.
13
Aufgabe 3:
Es sei H die Halbkreisscheibe über einer Strecke AB, und C sei ein Punkt in H.
Das Dreieck DEF bestehe aus dem Fußpunkt des Lotes von C auf AB sowie aus
den Schnittpunkten E bzw. F des Halbkreises mit der Geraden durch C und A
bzw. durch C und B. Stellen Sie über die Lage von C in DEF eine möglichst starke
Vermutung auf, und beweisen Sie diese.
Heuristische Methode:
Als “Ortslinie” oder “geometrischer Ort” bezeichnet man die Menge aller Punkte, die bestimmten Bedingungen genügen. Bei der Methode der Ortslinien (Schema
zweier geometrischer Örter) wird ein geometrisches Problem zunächst auf die Konstruktion eines Punktes reduziert und dann die Bedingung so in zwei Teile zerlegt,
dass jeder Teil eine Gerade oder einen Kreis als Ortslinie für den unbekannten Punkt
ergibt.
Aufgabe 4:
Es sind zwei Dreiecke zu konstruieren, von denen
i) a, ha (Höhe auf a) und α bzw.
ii) a, α und r (Radius des Inkreises)
gegeben sind.
Aufgabe 5:
Bestimmen Sie innerhalb eines gegebenen Dreiecks ABC, dessen Winkel kleiner als
120◦ sind, einen Punkt P , von dem aus alle drei Seiten unter dem gleichen Winkel
erscheinen. Suchen und beweisen Sie eine Eigenschaft der Umkreismittelpunkte von
ABP , BCP und CAP .
Aufgabe 6:
Gegeben seien zwei parallele Geraden g, h und ein Punkt P mit gleichem Abstand
von g und h. Gesucht wird die Ortslinie des dritten Eckpunkts C aller gleichseitigen
Dreiecke ABC mit A auf g, B auf h und P auf AB (vgl. Aufgabe 2).
[Hinweis: Betrachten Sie die Thales-Halbkreise durch P über AC und BC.] (Achtung: Zwei disjunkte Linien.)
Heuristische Methode:
Methode der ähnlichen Figuren : Wenn man die gesuchte Figur nicht konstruieren
kann, erwäge man die Konstruktion einer ähnlichen Figur.
Aufgabe 7:
Es sind zwei Dreiecke zu konstruieren, von denen
i) sa , sb und sc bzw.
ii) ha , hb und hc
gegeben sind. [Hinweis: In beiden Fällen können mathematische Zusammenhänge
verwendet werden.]
Aufgabe 8:
Auf den Seiten AB und BC eines gegebenen Dreiecks ABC, dessen Winkel kleiner
als 120 ◦ sind, seien nach außen gleichseitige Dreiecke AQB und BRC errichtet.
Suchen und beweisen Sie eine Beziehung zwischen den Strecken AR und CQ sowie
eine Eigenschaft ihres Schnittpunkts T .
14
Aufgabe 9:
Im Dreieck ABC seien a, b, c die Seitenlängen, hc die Länge der Höhe auf AB und
R der Radius des Umkreises.
i) Zeigen Sie, dass 2 hc R = ab gilt, indem Sie zwei geeignete ähnliche Dreiecke
verwenden.
ii) Bestimmen Sie den Flächeninhalt des Dreiecks ABC mit Hilfe von a, b, c und R.
Heuristische Methoden:
Methode der Hilfslinien und Hilfsfiguren : Man versuche, Hilfslinien zu finden, die
schon bekannte Zusammenhänge ins Spiel bringen. Vorwärts- und rückwärtsschließend, mit ähnlichen Situationen vergleichend und Hypothesen aufstellend schaffe
man Pfeiler, die geeignet sein können, eine Brücke zwischen den gegebenen Daten und dem Ziel zu tragen. Dabei ist auch zu bedenken, dass oft “psychologische
Blöcke” auftreten, weil Hilfslinien den (angenommenen) Rahmen der Ausgangsfigur
überschreiten können.
Aufgabe 10:
Es seien f, g, h drei Geraden, die sich in drei verschiedenen Punkten schneiden. Bestimmen Sie die Menge der Punkte, für die die Fußpunkte der Lote auf f, g und h
kollinear sind.
[Hinweis: Versuchen Sie, geeignete Winkelbeziehungen zu finden, indem Sie Verbindungsstrecken und Kreise zu Hilfe nehmen. Unterscheiden Sie dabei die verschiedenen Bereiche, in die die Ebene durch die Geraden zerlegt wird.]
Aufgabe 11:
Konstruieren Sie innerhalb eines gegebenen Dreiecks ABC, dessen Winkel kleiner
als 120 ◦ sind, denjenigen Punkt T , dessen Abstandssumme |AT | + |BT | + |CT |
minimal ist. [Hinweis: Beachten Sie Aufgabe 8, und suchen Sie zwischen zwei festen
Punkten einen Streckenzug mit den Teilstreckenlängen |AT |, |BT | und |CT |.]
Aufgabe 12:
Es sei U der Umkreis eines spitzwinkligen Dreiecks ABC, und Ka , Kb , Kc seien
die Kreisbögen, die durch Spiegelung der Teilkreisbögen von U an den zugehörigen
Seiten von ∆ABC entstehen. Stellen Sie eine möglichst starke Vermutung über den
Durchschnitt von Ka , Kb und Kc auf und beweisen Sie diese.
Heuristische Methoden:
Methode der Problemvariation (Abwandlungsstrategie, Verallgemeinerungsstrategie): Man suche nach Zusammenhängen, die zu erkennen sind, wenn ein geeigneter
Parameter variiert wird.
Methode der Symbolisierung : Häufig vereinfacht sich ein Problem durch die geschickte Wahl von Bezeichnungen.
Rückwärtsstrategie : Man nehme das Problem als gelöst an und versuche mit umkehrbaren Schlüssen die gegebenen Daten oder bekannte Aussagen zu erreichen. Die
Lösung erfolgt dann auf dem umgekehrten Weg.
Aufgabe 13:
Es sei ABC ein spitzwinkliges Dreieck, D und E seien von A , B , C verschiedene
Punkte auf AB bzw. BC , und P sei ein Punkt im Innern von ∆ABC auf dem
Umkreis von ∆BED . Zeigen Sie, dass der von P verschiedene Schnittpunkt der
Umkreise von ∆ADP und von ∆CP E auf der Verbindungsgeraden von A und C
liegt.
15
Aufgabe 14:
Es sei H ein Halbkreis über einer Strecke AB und K ein Kreis, der AB in E und
H in F berührt.
i) Zeigen Sie, dass die Mittelpunkte aller möglichen Kreise K auf einer Parabel
liegen.
ii) Es sei D der Schnittpunkt von H mit derjenigen auf AB senkrecht stehenden
Tangente an K , die AB zwischen A und E schneidet. Beweisen Sie, dass dann
|AD| = |AE| gilt.
[Hinweis: Nach Einführung geeigneter Bezeichnungen kann der Satz von Pythagoras
mehrmals angewendet werden. ]
Aufgabe 15:
Zeigen Sie, dass die drei Schnittpunkte der benachbarten Winkeldreiteilenden eines
beliebigen Dreiecks stets ein gleichseitiges Dreieck bilden. [Hinweis: Gehen Sie von
einem gleichseitigen Dreieck P QR aus, und errichten Sie über den Seiten nach außen
gleichschenklige Dreiecke P 0 QR, Q 0 RP und R 0 P Q , deren Basiswinkel ζ, η und ϑ
den Beziehungen ζ+η+ϑ = 120◦ , ζ < 60◦ , η < 60◦ und ϑ < 60◦ genügen. Verlängern
Sie die Schenkel über die jeweilige Basis hinaus, bis sie sich in den Punkten A, B
und C schneiden. Suchen Sie dann geeignete Winkelbeziehungen. Dabei benötigen
Sie noch einmal Rückwärtsstrategie! ]
Aufgabe 16:
Es sei ABC ein spitzwinkliges Dreieck, D, E und F seien von A , B , C verschiedene
Punkte auf AB, BC bzw. AC, und KA , KB , KC seien die Umkreise von ∆ADF ,
∆BED bzw. ∆CF E .
i) Zeigen Sie, dass der von D verschiedene Schnittpunkt P von KA und KB auf F Q
liegt, wobei Q der von B verschiedene oder mit B zusammenfallende Schnittpunkt
von KB mit der Parallelen zu AC durch B ist. [Achtung: Es ist zu unterscheiden,
ob die Parallele den Kreis KB berührt oder schneidet.]
ii) Beweisen Sie mit Hilfe von i), dass sich KA , KB und KC in einem Punkt
schneiden.
Aufgabe 17:
In den Aufgaben 5, 8 und 11 der Übungen zur Geometrie findet sich eine Sequenz zur
Entdeckung des in Aufgabe 11 erklärten “Fermat-Torricelli-Punktes” (FT-Punkt).
Dabei ist es unbefriedigend, dass der 120◦ -Punkt (in Aufgabe 5) und die Rolle von
Q und R (in Aufgabe 8) “verraten” wurden.
Beschreiben Sie eine “experimentelle” Entdeckungssequenz, bei der dieses vermieden wird, indem Sie annehmen, dass ein Geometrieprogramm (z.B. EUKLID) zur
Verfügung steht, das zu Dreieckspunkten A, B und C , die die Bedingung von Aufgabe 11 erfüllen, jeweils den FT-Punkt angibt und markieren lässt.
[Hinweis: Steuern Sie Vermutungen zu folgenden Schritten an: i) Ortslinie der FTPunkte bei fester Grundseite AB ; ii) Ortslinie der Eckpunkte C mit festbleibendem
FT-Punkt T ; iii) Schnittpunkt S der Ortslinien aus ii); iv) Form des Dreiecks ABS ;
v) Drehung des Dreiecks ABT um A bzw. B mit Drehwinkel 60◦ .]
Die folgenden drei Aufgaben wurden in den vergangenen beiden Jahren im “Bundeswettbewerb Mathematik” gestellt. SchülerInnen haben für vier Aufgaben rund
zwei Monate Zeit. Versuchen Sie wenigstens herauszufinden, welche heuristischen
Strategien zum Ziel führen können.
16
Aufgabe 18:
Über den Seiten BC und CA eines beliebigen Dreiecks ABC werden nach außen
Quadrate errichtet. Der Mittelpunkt der Seite AB sei M, die Mittelpunkte der
beiden Quadrate seien P und Q.
Man beweise, dass das Dreieck M P Q gleichschenklig-rechtwinklig ist.
Aufgabe 19:
Gegeben seien ein Dreieck ABC und ein Punkt P auf der Seite AB mit folgenden
Eigenschaften:
(1) |BC| = |AC| + 21 · |AB| ,
(2) |AP | = 3 · |P B|.
Man beweise: Der Winkel P AC ist doppelt so groß wie der Winkel CP A.
Aufgabe 20:
In einer Ebene werden auf dem geraden Streckenzug ABC über AB , BC und CA
als Grundseiten die positiv orientierten gleichschenkligen Dreiecke ABS1 , BCS2
und CAS3 mit den Basiswinkeln 30◦ errichtet.
Man beweise: Das Dreieck S3 S2 S1 ist gleichseitig.
9
Dynamische Geometrieprogramme
Hier sollen später die folgenden “dynamischen Geometrieprogramme” und ihre Einsatzmöglichkeiten beschrieben werden:
CABRI (Webseiten: http://education.ti.com/product/software/cabri/
features/features.html und http://www.cabri.net/index-e.html)
Cinderella (Webseite: http://www.cinderella.de/de/)
EUKLID (Webseite: http://www.dynageo.de)
GEOLOG (Auslieferung: DÜMMLER VERLAG, Kaiserstr. 31-37, 53113 Bonn)
10
Literatur zu den Vorlesungen “Geometrie” und
“Didaktik der Geometrie” (WS 1999/2000)
Geometrie:
[1] Coxeter, H. S. M.: Unvergängliche Geometrie, Birkhäuser Verlag Basel e.a. 1963
(vergriffen).
[2] Coxeter, H. S. M. u. S. L. Greitzer: Zeitlose Geometrie, Klett Studienbücher,
Ernst Klett Verlag Stuttgart 1983 (vergriffen).
[3] Hilbert, David: Grundlagen der Geometrie. B. G. Teubner Stuttgart, (14. Auflage
erscheint Ende 1999 : 70,00 DM).
[4] Hilbert, David u. Stefan Cohn-Vossen: Anschauliche Geometrie,
Springer Verlag Berlin e.a. 19962 (68,00 DM).
[5] Holland, Gerhard: Geometrie in der Sekundarstufe, Spektrum Akademischer
Verlag Heidelberg 19962 (38,00 DM).
17
[6] Koecher, Max u. Aloys Krieg: Ebene Geometrie, Springer Verlag Berlin e.a. 1993
(Nachdruck ist geplant: 44,00 DM)
[7] Mainzer, Klaus: Geschichte der Geometrie, BI Wissenschaftsverlag Mannheim
e.a. 1980 (vergriffen).
[8] Mitschka, Arno: Didaktik der Geometrie in der Sekundarstufe I, Herder Verlag
Freiburg e.a. 1982 (vergriffen).
[9] Schumann, Heinz: Schulgeometrisches Konstruieren mit dem Computer, Computerpraxis im Unterricht, J.B. Metzler u. B.G. Teubner Stuttgart 1991 (vergriffen).
[10] Schupp, Hans: Kegelschnitte, BI Wissenschaftsverlag Mannheim e.a. 1988 (34,00
DM: Neuauflage erscheint bei Spektrum Akademischer Verlag Heidelberg).
[11] Struve, Horst: Grundlagen einer Geometriedidaktik, Spektrum Akademischer
Verlag Heidelberg 1990 (läuft aus, 38,00 DM).
Mathematikdidaktik:
[12] Engel, Arthur: Problem-Solving Strategies, Springer Verlag New York e.a. 1998
(68,00 DM).
[13] Führer, Lutz: Pädagogik des Mathematikunterrichts (Eine Einführung in die
Fachdidaktik für Sekundarstufen), Verlag Vieweg Wiesbaden 1997 (49,80 DM).
[14] Winter, Heinrich: Entdeckendes Lernen im Mathematikunterricht (Einblicke in
die Ideengeschichte und ihre Bedeutung für die Pädagogik), Verlag Vieweg Wiesbaden 19912 (49,80).
[15] Wittmann, Erich: Grundfragen des Mathematikunterrichts, Verlag Vieweg Wiesbaden 19978 (39,80 DM).
(Philosophie der) Mathematik:
[16] Davis, Philip J. u. Reuben Hersh: Erfahrung Mathematik, Birkhäuser Verlag
Basel e.a. 19962 (49,80 DM).
18