Mathematik * Jahrgangsstufe 7 * Winkelberechnungen

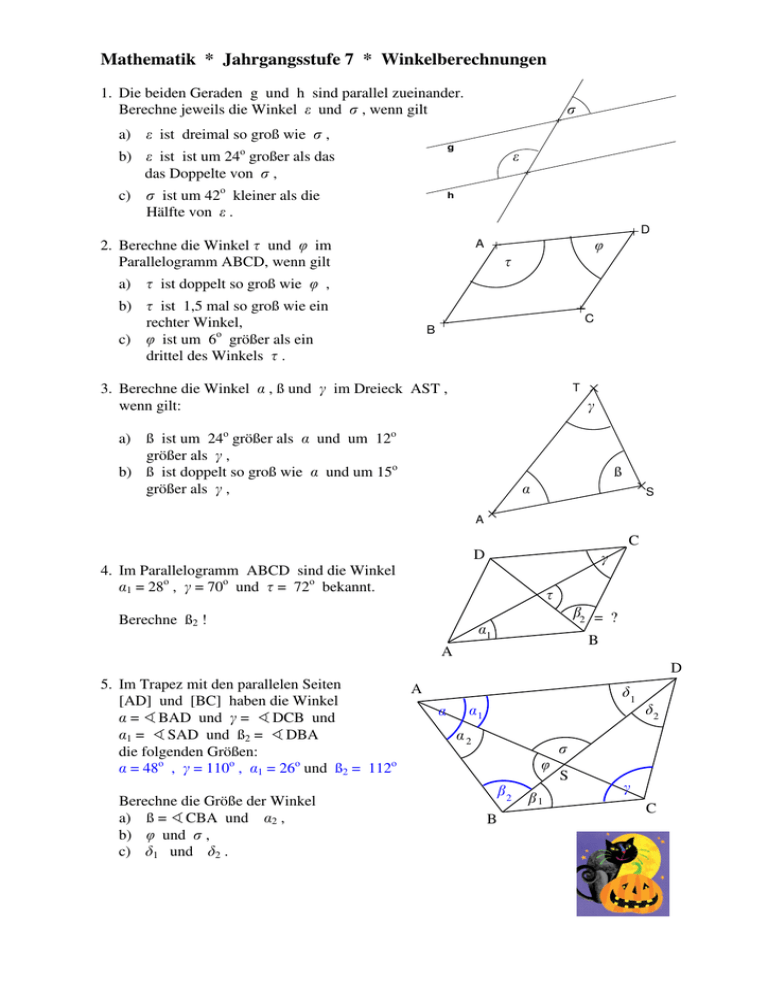
Mathematik * Jahrgangsstufe 7 * Winkelberechnungen
1. Die beiden Geraden g und h sind parallel zueinander.
Berechne jeweils die Winkel und , wenn gilt
a) ist dreimal so groß wie ,
g
b) ist ist um 24o großer als das
das Doppelte von ,
c) ist um 42o kleiner als die
Hälfte von .
h
D
2. Berechne die Winkel und im
Parallelogramm ABCD, wenn gilt
A
a) ist doppelt so groß wie ,
b) ist 1,5 mal so groß wie ein
rechter Winkel,
c) ist um 6o größer als ein
drittel des Winkels .
C
B
3. Berechne die Winkel , ß und im Dreieck AST ,
wenn gilt:
T
a) ß ist um 24o größer als und um 12o
größer als ,
b) ß ist doppelt so groß wie und um 15o
größer als ,
ß
S
A
C
D
4. Im Parallelogramm ABCD sind die Winkel
1 = 28o , = 70o und = 72o bekannt.
Berechne ß2 !
2 = ?
1
B
A
D
5. Im Trapez mit den parallelen Seiten
A
[AD] und [BC] haben die Winkel
= ŒBAD und = ŒDCB und
1 = ŒSAD und ß2 = ŒDBA
die folgenden Größen:
= 48o , = 110o , 1 = 26o und ß2 = 112o
Berechne die Größe der Winkel
a) ß = ŒCBA und 2 ,
b) und ,
c) 1 und 2 .
1
1
2
2
2
B
1
S
C
Mathematik * Jahrgangsstufe 7 * Winkelberechnungen * Lösungen
1. Bei allen Teilaufgaben gilt: (1) + = 180o
zusätzlich gilt (2) = 3 $ a) (1) + = 180o
Setzt man (2) in (1) ein, so erhält man
3 $ + = 180o e 4 $ = 180o e = 45o und
= 3 $ = 135o
b) (1) + = 180o
zusätzlich gilt (2) = 2 $ + 24o
Setzt man (2) in (1) ein, so erhält man
2 $ + 24o + = 180o e 3 $ = 156o e = 52o und = 2 $ +24o = 128o
c) (1) + = 180o
zusätzlich gilt (2) = 0,5 $ - 42o
Setzt man (2) in (1) ein, so erhält man
+ 0,5 $ - 42o = 180o e 1,5 $ = 222o e = 148o und
= 0,5 $ - 42o = 32o
2. Bei allen Teilaufgaben gilt: (1) + = 180o
a) (1) + = 180o zusätzlich gilt (2) = 2 $ Setzt man (2) in (1) ein, so erhält man
2 $ + = 180o e 3 $ = 180o e = 60o und = 2 $ = 120o
b) (1) + = 180o zusätzlich gilt (2) = 1,5 $ 90o also = 135o
und damit = 180o - = 45o
c) (1) + = 180o zusätzlich gilt (2) = 6o + : 3 = 6o + 1/3 Setzt man (2) in (1) ein, so erhält man
+ 6o + 1/3 = 180o e 4/3 = 174o e = 130,5o
3. Bei allen Teilaufgaben gilt: (1) + ß + = 180o
a) (1) + ß + = 180o zusätzlich gilt (2) ß = 24o + und (3) ß = 12o + e (2) = ß - 24o und (3) = ß - 12o
Setzt man (2) und (3) in (1) ein, so erhält man
ß - 24o + ß + ß - 12o = 180o e 3 ß = 216o e ß = 72o und = 48o und = 60o
b) (1) + ß + = 180o zusätzlich gilt (2) ß = 2 $ und (3) ß = 15o + e (2) = 0,5 $ ß und (3) = ß - 15o
Setzt man (2) und (3) in (1) ein, so erhält man
0,5 $ ß + ß + ß - 15o = 180o e 2,5 $ ß = 195o e ß = 78o und = 39o und = 63o
C
α1 + α 2 = γ ⇒ α 2 = γ − α1 = 70o − 28o = 42o
4.
D
σ + τ = 180o ⇒ σ = 180o − τ = 180o − 72o = 108o
α1 + β1 + σ = 180o ⇒ β1 = 180o − α1 − σ = 44o
2
1
β1 + β2 + γ = 180o ⇒ β2 = 180o − γ − β1 ⇒
ß 2 = 180o − 70o − 44o = 66o
5. a)
A
α + β = 180o ⇒ β = 180o − α = 180o − 48o = 132o
α1 + α 2 = α ⇒ α 2 = α − α1 = 48o − 26o = 22o
b)
α 2 + β2 + ϕ = 180o ⇒ ϕ = 180o − α 2 − β2 = 180o − 22o − 112o = 46o
c)
σ + ϕ = 180o ⇒ σ = 180o − ϕ = 180o − 46o = 134o
α1 + δ1 + σ = 180o ⇒ δ1 = 180o − α1 − σ = 180o − 26o − 134o = 20o
β1 + β2 = β ⇒ β1 = β − β2 = 132o − 112o = 20o
β1 + γ + δ2 = 180o ⇒ δ2 = 180o − β1 − γ = 180o − 20o − 110o = 50o
= ?
1
2
B