Das elektrische Potential eines Dipols ist

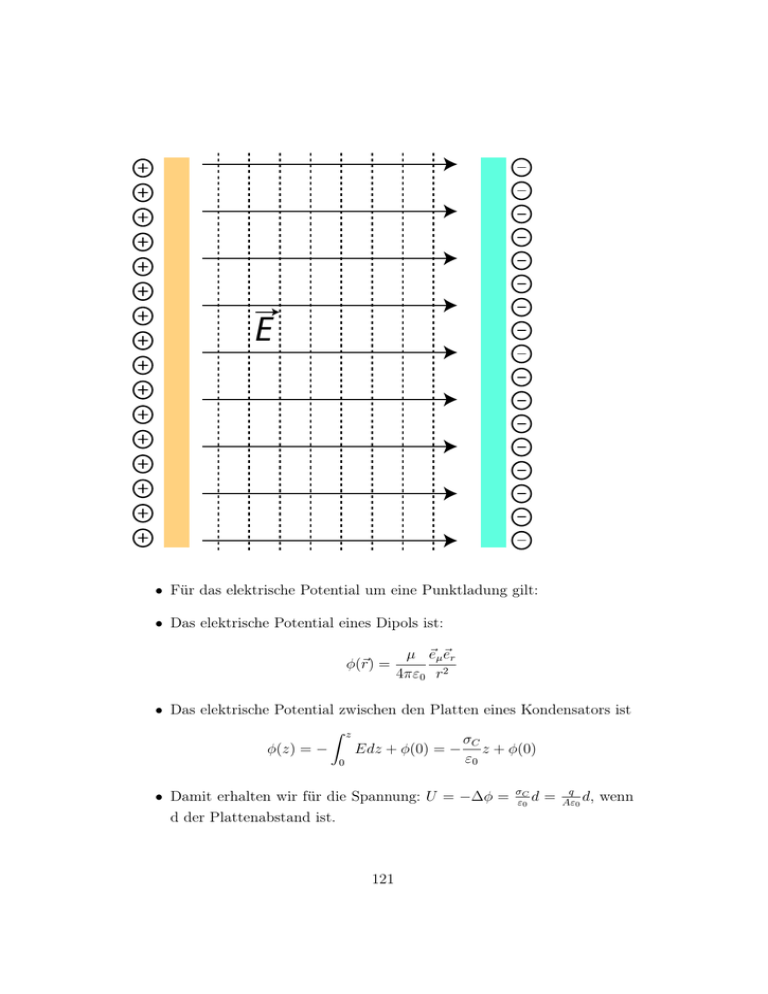
E
• Für das elektrische Potential um eine Punktladung gilt:
• Das elektrische Potential eines Dipols ist:
φ(~r) =
µ ~eµ~er
4πε0 r2
• Das elektrische Potential zwischen den Platten eines Kondensators ist
Z z
σC
φ(z) = −
Edz + φ(0) = − z + φ(0)
ε0
0
• Damit erhalten wir für die Spannung: U = −∆φ =
d der Plattenabstand ist.
121
σC
d
ε0
=
q
d,
Aε0
wenn
5.1.6
Die Kapazität
• Der Quotient aus Ladung und Spannung an einem Kondensator
q
:= C
U
wird Kapazität C genannt mit der Einheit CV−1 = F (Farad nach Michael Faraday (* 22. September 1791 in Newington Butts bei London;
† 25. August 1867 bei Hampton Court)).
• Der Plattenkondensator hat eine Kapazität von C =
Aε0
d
• Parallelschaltung: Flächen addieren sich, also Cges = C1 + C2
• Reihenschaltung: Abstände addieren sich, also
1
Cges
=
• Für die Feldstärke im Kondensator gilt demnach E =
1
C1
+
1
C2
U
.
d
• Für die Arbeit, die beim Aufladen des Kondensators verrichtet wird,
gilt:
Z
Z
1 q2
1
Wel = qdU = C U dU = CU 2 =
2
2C
• Diese Energie ist jetzt im Innern des Kondensators mit dem Volumen
1
V = Ad gespeichert. Die Energiedichte beträgt also wel = 2Ad
CU 2 =
1
ε E 2.
2 0
5.1.7
Materie im elektrischen Feld
• Wenn wir Materie im elektrischen Feld betrachten, so besteht diese
aus Atomen, welche wiederum aus positiv geladenen Atomkernen und
negativ geladenen Elektronen bestehen.
• Prinzipiell können wir jetzt zwei Arten von Materie unterscheiden: Leiter und Nichtleiter. Im Leiter können Ladungen über makroskopische
Distanzen wandern, im Nichtleiter hingegen können Ladungen nur mikroskopisch aus ihrer Ruhelage verschoben werden.
122
Leiter
• In einem Leiter werden Ladungen sicher so lange verschoben, wie ein
elektrisches Feld existiert. Betrachten wir jetzt einen Leiter im elektrischen Feld, so wird es dort zu einer Ladungstrennung kommen: die
beweglichen Ladungen wandern aufgrund der auf sie ausgeübten Kraft.
Diese Wanderung endet erst an der Oberfläche des Körpers. Diese Ladungstrennung im elektrischen Feld nennt man Influenz.
• Durch die Ladungstrennung bildet sich ein elektrisches Feld aus, das
dem äusseren elektrischen Feld entgegeng gerichtet ist. Die Wanderung
wird so lange anhalten, bis das interne Feld das äussere vollständig
kompensiert. Im innern eines elektrischen Leiters gibt es kein
makroskopisches elektrisches Feld.
• Das gilt nicht nur für massive Leiter, sondern auch für Hohlräume, die
von einem Leiter umschlossen sind. Einen solchen Hohlraum nennt man
Faraday–Käfig. Ein Auto ist ein solcher Farady–Käfig, weswegen man
bei Gewitter im Auto ungefährdet ist.
123
• Eine weitere Konsequenz der Beweglichkeit der Ladungen ist, dass das
elektrische Feld stets senkrecht zur Oberfläche des Leiters orientiert
ist. Wäre das nicht der Fall, gäbe es eine Komponente des elektrischen
Feldes parallel zum Leiter, die zu einer Ladungsverscheibung führen
würde, bis das Feld wiederum senkrecht auf dem Leiter stehen würde.
Nichtleiter
• Im Nichtleiter führt ein äusseres elektrisches Feld zu einer Verschiebung
der Ladungen aus der Ruhelage oder zur Drehung etwaiger elektrischer
Dipole. Auch hier bildet sich ein inneres Feld aus, das dem äusseren
entgegenwirkt, allerdings kann dieses nicht so gross werden, dass es das
äussere kompensiert.
124
• Den Quotienten aus den Feldstärken des von aussen angelegten und
des inneren Feldes EEAI := ε nennt man Dielektrizitätszahl. Das Feld im
innern ist also im Vergleich zu dem Feld im Vakuum um den Faktor ε
reduziert.
• Auch die Verschiebung der Ladungen führt zu einer Flächenladungsdichte auf der Oberfläche des Dielektrikums, man sagt auch, zu einer Polarisation. Das durch die Flächenladungsdichte P erzeugte Feld
E = εP0 ist dem äusseren Feld entgegen gerichtet, so dass wir erhalten:
EI = EA −
P
ε0
• Dabei wird P als Polarisation bezeichnet. Betrachten wir jetzt einen
125
Kondensator, in den wir ein Dielektrikum einbringen, so reduziert sich
bei konstanter Ladung und konstantem Plattenabstand die Spannung
um den Faktor ε, das heisst, die Kapazität erhöht sich um den Faktor
ε:
A
C = εε0
d
• Zellmembranen sind in guter Näherung Nichtleiter, während das Zytoplasma und das Ektoplasma leitfähig sind. Demzufolge kann eine Zelle
als Kondensator aufgefasst werden, und Messungen der Kapazität erlauben Rückschlüsse über die Zusammensetzung der Zellmembran.
Piezoelektrizität
• Die Verschiebung der Ladungen infolge eines äusseren elektrischen Feldes kann zu einer Verformung des Körpers führen.
• Umgekehrt kann natürlich die Deformation eines Körpers zur Verschiebung von Ladungen führen, so dass ein elektrisches Feld entsteht.
• Diesen, meist bei Kristallen beobachteten Effekt bezeichnet man als
piezoelektrischen Effekt.
• Anwendung findet er z.B. in elektronischen Feuerzeugen bzw. der Umkehreffekt bei der Nanopositionierung. Darunter versteht man die auf
10−9 m genaue Positionierung, die zum Beispiel in Rastermikroskopen
zum Einsatz kommt.
126
5.2
Der stationäre elektrische Strom
• Die Bewegung und damit den Transport von elektrischer Ladung unter
dem Einfluss eines elektrischen Feldes bezeichnen wir als elektrischen
Strom.
• Betrachten wir Ladungen im Vakuum (z.B. Elektronen), so wird die
auf die Ladungen wirkende Kraft zu einer Beschleunigung der Ladung
führen. In einem Leiter können sich die Ladungen (meist ebenfalls Elektronen) nicht ungehindert bewegen, da sie mit andern Teilchen Zusammenstösse erleiden, die zu einem Impulsübertrag führen. Die Zahl der
Zusammenstösse steigt sicher mit der Geschwindigkeit, weshalb ein Ansatz ähnlich der Stokes–Reibung für die Reibungskraft, die der Bewegung der Ladungen entgegen gerichtet ist, gerechtfertigt ist:
FR ∝ v
• Das heisst, die Ladung wird so lange beschleunigt, bis die Coulomb–
Kraft durch das elektrische Feld gleich der Reibungskraft ist, dann bewegt sie sich gleichförmig mit der sogenannten Driftgeschwindigkeit.
Das heisst, bei zeitlich konstantem elektrischen Feld werden die Ladungen eine konstante Geschwindigkeit haben, was wir mit dem Begriff
127
stationär beschreiben.
• Im stationären Fall gilt:
FC = FR ⇒ qE = κv ⇒ v =
q
E = uE
κ
wobei κ der Reibungskoeffizient und u die Beweglichkeit der Ladungsträger ist.
• Als Strom hatten wir bei der Hydrodynamik das durch eine Fläche
transportierte Volumen je Zeiteinheit betrachtet. Als elektrischen Strom
definieren wir die je Zeiteinheit durch eine Fläche transportierte Ladungsmenge:
Z
dqA
I :=
jC dA
=
dt
A
wobei jC die Ladungsstromdichte ist: jC = %C v mit v der Driftgeschwindigkeit. Die Einheit der elektrischen Stromstärke ist das Ampére
(abgekürzt A)
5.2.1
Der elektrische Strom in metallischen Leitern
• Betrachten wir den Stromfluss durch einen metallischen Leiter der Länge l mit dem Querschnitt A, so erhalten wir für den Stromfluss mit
E = U/l:
1
A
I = %C u U = U
l
R
• wobei R als ohmscher Widerstand bezeichnet wird. Dies ist das ohmsche Gesetz. Die Grösse r = %C1 u wird als spezifischer Widerstand bezeichnet, da er vom Stoff abhängig ist. Damit erhalten wir R = r Al .
• Die Arbeit, die der Stromfluss verrichtet, ist
∆Wel = ∆qU = U I∆t
128
und damit die Leistung
Pel =
∆Wel
= UI
∆t
• Reihenschaltung von Widerständen
• Parallelschaltung von Widerständen
• Wir betrachten im folgenden Netzwerke von elektrischen Leitern, bestehend aus miteinander verknüpften Leitern (mit Widerständen). Die
Elemente eines solchen Netzwerks werden als Knoten und Maschen beH
zeichnet. Die Gesetze der Ladungserhaltung jc dA = 0 sowie der WirH
belfreiheit des elektrischen Feldes Eds = 0 führen dann zu folgenden
Regeln (Kirchhoffsche Regeln):
1. Kirchhoffsche Regel: Knotenregel
• Die Summe der Ströme zu einem Knoten ist gleich der Summe der
Ströme, die vom Knoten weg gerichtet sind (Ladungserhaltung)
2. Kirchhoffsche Regel: Maschenregel
• Innerhalb einer Masche eines Netzwerks ist die Summe der Spannungsabfälle über den Widerständen gleich der Summe der sogenannen Urspannungen, das sind die Elemente, die das elektrische Feld aufbauen
(Energieerhaltung)
5.2.2
Der elektrische Strom in Flüssigkeiten
• Die Ladungsträger, die in Flüssigkeiten den Stromfluss realisieren, sind
positiv und negativ geladene Ionen. Eine Lösung von Ionen in einer
Flüssigkeit heisst Elektrolyt
• Zahl der Elementarladungen je Ion: Ladungszahl z
129
• Gesamtladung eines Mols von Ionen mit der z=1: F = eNA = 96486 C mol−1 ,
Faraday-Konstante
• Positive Ionen wandern zur negativ geladenen Elektrode (Kathode):
Kationen
• Negative Ionen wandern zur positiv geladenen Elektrode (Anode): Anionen
• Das Verhältnis von transportierter Ladung zur transportierten Masse
(2. Faraday-Gesetz):
∆q
zF
=
∆m
mM ol
• Der Elektrolyt zeigt ohmsches Verhalten:
U = UG + RI
wobei UG eine Grenzflächen–Spannung ist, die wir gleich kennenlernen
werden.
• Den spezifischen Widerstand des Elektrolyten können wir nun mit der
Konzentration und der Beweglichkeit der Ionen ausdrücken:
r=
5.2.3
1
zc(u+ − u− )F
Elektrische Grenzflächen
• Zwei Leiter im Kontakt: Unterschiedliche Austrittsarbeiten für Elektronen, es bildet sich eine Kontaktspannung
• Kein Strom, da sich die Kontaktspannungen kompensieren
• Bei unterschiedlichen Temperaturen der Kontakte: Thermospannung
Utherm = UKont (TA ) − UKont (TB )
• Temperaturmessung!
130
• Grenzschicht zwischen zwei Elektrolyten: Osmose führt versucht Konzentration auszugleichen. Kann nur eine Ionensorte die Membran passieren, bildet sich Membranpotential aus
• Es gehorcht der Nernst-Gleichung
UM emb =
RT c2
ln
zF c1
• In Zellen: Aktive Kanäle, die Ionen transportieren, untersuchbar mit
Patch-Clamp (Nobelpreis 1991 Neher und Sakmann)
• Grenzschicht zwischen Elektrolyt und Festkörper: chem. Reaktion (Redoxreaktion) führt zur Ausbildung einer Kontaktspannung. Verschiedene Stoffe haben unterschiedliche Kontaktspannungen. Auf diesem Prinzip beruhen die galvanischen Elemente (Batterien).
5.2.4
Der elektrische Strom in Gasen
• Auch in Gasen können Ladungsträger einen Stromfluss realisieren, und
zwar Ionen und Elektronen. Die Gasmoleküle müssen dazu ionisiert
werden, was durch Stösse, Wärme, sowie Bestrahlung mit ionisiernder
Strahlung geschehen kann.
131
A
• Anwendungen: Leuchtstoffröhre, Bogenlampen (Xenon-Scheinwerfer beim
Auto)
5.2.5
Der elektrische Strom im Vakuum
• Durch Injektion von Elektronen ins Vakuum können auch dort Ladungsträger durch ihre Bewegung einen Stromfluss realisieren.
A
132
• Anwendungen: Röhrendiode, Röhrentriode, Elektronenstrahloszilloskop,
Fernseher, Streak Kameras.
5.3
Magnetostatik
• Kraftwirkung zwischen bestimmten Erzen ist seit dem Altertum bekannt: Kraftwirkung zwischen Magneten
• Die magnetische Kraft kann abstossend und anziehend sein.
• Jedoch: Es gibt keine getrennten “magnetischen Ladungen”, teilen wir
einen Magneten, so hat er wieder Nord- und Südpol. Ein Magnet ist
also immer Dipol.
• Warum gibt es keine fünfte fundamentale Wechselwirkung “magnetische
Kraft”? Weil sich die magnetische Wechselwirkung auf die elektrische
zurückführen lässt (mit Hilfe der speziellen Relativitätstheorie).
5.3.1
Das magnetische Feld
Analog zum elektrischen Feld führen wir ein magnetisches Feld ein, um die
Wirkung auf einen elektrischen Dipol beschreiben zu können. Da es keine
magnetische Ladung gibt, betrachten wir das magnetsiche Feld eines Dipols.
Die magnetische Flussdichte eines solchen Dipols ist:
~ = p~µ0 3(~ep · ~er )~er − ~ep
B
4π
r3
Vs
Die Einheit der magnetischen Flussdichte ist das Tesla, T = m
2 . Teilen wir
die magnetische Flussdichte durch die magnetische Feldkonstante µ0 , so er~ = B/µ
~ 0 mit der Einheit V/m. Die
halten wir die magnetische Feldstärke H
magnetische Flussdichte multipliziert mit der Fläche ergibt den magnetischen
~ ·A
~ mit der Einheit Weber, Wb = Vs.
Fluss ΦB = B
In einem homogenen Magnetfeld wirkt auf einen Magneten (der stets ein
Dipol ist) keine resultierende Kraft, sondern lediglich ein Drehmoment.
133
Da es keine magnetischen Monopole gibt, hat das magnetische Feld keine
Quellen und keine Senken; das Oberflächenintegral der magnetischen Flussdichte über eine geschlossene Oberfläche ist also stets gleich Null:
I
~ A
~=0
Bd
A
5.3.2
Die Lorentz-Kraft
Auf ein eine bewegte Ladung wirkt in einem Magnetfeld eine Kraft, die
Lorentz-Kraft:
~
F~ = q~v × B
Da es sich um ein Kreuzprodukt handelt, steht die Kraft stets senkrecht
auf der magnetsichen Flussdichte und auf der Geschwindigkeit. Ohne den
Einfluss weiterer äusserer Kräfte führt ein geladenes Teilchen im Magnetfeld
also eine Kreisbewegung aus. Für die Wirkung der Kraft ist die senkrecht
~ stehende Komponente des Magnetfeldes verantwortlich, bei ~v k B
~
auf B
verschwindet die Lorentz-Kraft. Letztendlich resultiert die Lorentz-Kraft aus
der elektrischen Kraft und aus der speziellen Relativitätstheorie.
Befindet sich ein stromdurchflossener Leiter in einem Magnetfeld, so führt
die Lorentz-Kraft zu einer Ladungstrennung und damit zu einer Spannung
senkrecht zum Stromfluss. Dieser Effekt wird Hall-Effekt genannt.
134
B
I
UH
Die Hall-Spannung UH hängt von der Stromstärke I, der magnetischen Flussdichte B, der Dichte der Ladungsträger %C sowie der Dicke d des Leiters in Richtung des Magnetfeldes ab:
UH = −
1 B
I
%C d
Der Hall-Effekt erlaubt es, magnetische Flussdichten zu messen.
Eine weitere Anwendung der Lorentz-Kraft ist im Massenspektrometer realisiert. Dazu wird die zu untersuchende Probe auf geeignete Art ionisiert.
Diese Ionen werden in einem elektrischen Feld beschleunigt und treten in ein
Magnetfeld, das senkrecht zur Geschwindigkeit orientiert ist, ein. Der Radius der Kreisbahn hängt von dem Verhältnis aus Ladung und Masse der
Ionen ab. Auf diese Weise kann die chemische Zusammensetzung einer Probe
untersucht werden.
135
Moderne Massenspektrometer basieren häufig auf Effekten im elektrischen
Feld (Quadrupol-MS, MALDI-TOF)
5.3.3
Elektrischer Strom und Magnetfeld
Ein elektrischer Strom ist stets mit einem Magnetfeld verbunden. Um einen
geraden Leiter bilden die magnetischen Feldlinien Kreise, wobei der Umlaufsinn nach der “rechte-Hand-Regel” bestimmt wird: zeigt der Daumen der
rechten Hand in Richtung des Stromflusses, so zeigen die gekrümmten Finger
in die Richtung des magnetischen Feldes.
I
Wickeln wir einen Leiter zu einer Spule der Länge l mit n Windungen auf,
so entsteht im Inneren ein nahezu homogenes magnetisches Feld:
H=
nI
nI
,B=
µ0
l
l
Anwendungen finden Elektromagnete in Elektromotoren sowie in der Kern136
resonanzspektroskopie sowie -tomographie. Ausserdem kann über die Kraftwirkung eines Elektromagneten die Stromstärke gemessen werden.
5.3.4
Materie im magnetischen Feld
Ähnlich wie sich elektrische Dipole im elektrischen Feld ausrichten, richten
sich magnetische Dipole im magnetischen Feld aus. Diese Ausrichtung kann
jedoch im Gegensatz zum elektrischen Feld auch zu einer Vergrösserung des
magnetischen Flusses und der magnetischen Feldstärke führen. Für die magnetische Flussdichte im Inneren eines Körpers gilt:
Bin = µBaus
wobei die Permeabilitätszahl µ mit der magnetischen Suszeptibilität χmagn
~ eines Materials
über µ = 1 + χmagn zusammenhängt. Die Magnetisierung M
ist analog zur Polarisation definiert:
~ in = B
~ aus + M
~ µ0
B
Die magnetischen Eigenschaften des Materials werden durch χmagn charakterisiert, und zwar bezeichnen wir das Material für −1 < χmagn ≤ 0 als
diamagnetisch, für 0 < χmagn als paramagnetisch und für 0 χmagn als ferromagnetisch. In einem dimagnetischen Material ist die magnetische Flussdichte also kleiner als im Aussenraum, in einem paramagnetischen etwa so wie
im Aussenraum, und in einem ferromagnetischen deutlich grösser als im Aussenraum.
5.4
Zeitlich veränderliche Felder
Bisher hatten wir uns im wesentlichen mit zeitlich konstanten Feldern und
Strömen beschäftigt. Nun wollen wir sehen, was passiert, wenn wir diese
Beschränkung aufheben.
137
5.4.1
Die magnetische Induktion
Bewegen wir einen Leiter in einem magnetischen Feld mit einem Geschwindigkeitsvektor, der eine senkrecht zum magnetischen Fluss stehende Komponente hat, wird eine Lorentz-Kraft auf die in dem Leiter befindlichen Ladungsträger ausgeübt. Es bildet sich demzufolge eine Spannung an den Enden des
Leiters bzw., wenn wir eine geschlossene Leiterschleife betrachten, zu einem
Stromfluss. Eine detaillierte Untersuchung ergibt, dass in einer geschlossenen Leiterschleife immer dann ein Strom fliesst, wenn sich der magnetsche
R
~ A
~ durch diese Schleife zeitlich ändert, sei es durch eine BeFluss ΦB = Bd
wegung der Schleife oder durch eine Änderung der Flussdichte. Es gilt das
Faradaysche Induktionsgesetz:
Uind = −
dΦB
dt
Das negative Vorzeichen ist Ausdruck der Lenzschen Regel: Der durch die
Bewegung induzierte Strom führt seinerseits zu einem magnetischen Feld,
das der Ursache der Bewegung entgegenwirkt.
138
B
v
UInd
Anwendung findet die Induktion in Generatoren, im Fahrraddynamo, und
auch bei der Messung von Bewegungen.
5.4.2
Die Selbstinduktion
Ein zeitlich veränderlicher Strom durch eine Leiterschleife führt zu einem sich
zeitlich verändernden Magnetfeld, das wiederum zur Induktion einer Spannung mit einem daraus resultierenden Stromfluss führt. Würde dieser Strom
in die gleiche Richtung fliessen wie der ursprüngliche, käme es zu Verstärkung
des Stromflusses über alle Massen, was der Energieerhaltung zuwider liefe.
Die in der Leiterschleife induzierte Spannung führt also zu einem verringerten Stromfluss. Die in einer Spule mit n Leiterschleifen induzierte Spannung
beträgt
A dI
Uind = −n2 µµ0
l dt
139
Die apparativen Daten können wir zusammenfassen:
Uind = −L
dI
dt
wobei L die Induktivität der Spule mit der Einheit
ry) ist.
140
V
A/s
=
Vs
A
=
Wb
A
= H (Hen-