Geometrie in der Ebene

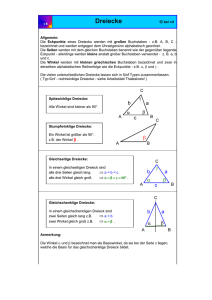
Winkel
Dreiecke
Winkel an geschnittenen Parallelen
Nebenwinkel
Scheitelwinkel
Stufenwinkel
Wechselwinkel
Sätze am Dreieck
Dreiecksarten
Dreiecksungleichung,
Seiten-Winkel-Beziehung
Flächeninhalt und Umfang
Geometrie in der Ebene
Vierecke
Parallelogramme
Drachenvierecke
Trapeze
Winkel
Wiederholung: Winkel
• Zwei Strahlen mit gemeinsamen Anfangspunkt S bezeichnet man als Winkel.
• Sie werden mit griechischen Buchstaben bezeichnet.
• Es gibt folgende Winkelarten
1. Spitzer Winkel
α
1° bis 89°
2. Rechter Winkel
γ
90°
3. Stumpfer Winkel
β
91° bis 179°
4. Gestreckter Winkel
δ
180°
5. Überstumpfer Winkel
ε
181° bis 359°
6. Vollwinkel
λ
360°
Schenkel
Scheitelpunkt S
α
δ
β
Übung
γ
ε
λλ
Winkel zeichnen
Aufgabe: Zeichne einen Winkel. α = 35°
Aufgabe: Zeichne folgende Winkel!
Gib die Winkelart an!
24°; 100°; 180° ;210°;
Winkel messen
1. Lege das Geodreieck im Scheitelpunkt so an,
dass ein Schenkel unten anliegt.
2. Lies bei dem zweiten Schenkel den Winkel ab.
Achte auf die richtige Wahl der Skale.
Scheitel- und Nebenwinkel
Scheitelwinkel
β=δ
α=γ
Nebenwinkel
α + β = 180°
γ + δ = 180°
Merke: 1. Winkel, die an zwei sich schneidenden Geraden gegenüber liegen,
heißen Scheitelwinkel. Sie haben den Scheitelpunkt gemeinsam.
Ihre Schenkel bilden Geraden.
2. Winkel, die an zwei sich schneidenden Geraden nebeneinander
liegen, heißen Nebenwinkel.
Scheitelwinkelsatz: Scheitelwinkel an zwei sich schneidenden Geraden sind
gleich groß.
Nebenwinkelsatz: Nebenwinkel an sich schneidenden Geraden ergänzen
sich zu 180°.
Übungen:
LB.S.152 Nr. 2a, 3 mündlich
2b
5, 6 Berechnung von Winkeln
Übung interaktiv 1
Übung interaktiv 2
Stufenwinkel und Wechselwinkel an geschnittenen
Parallelen
Wechselwinkel
x
x
x
x
x
Scheitelwinkel
Stufenwinkel
Stufenwinkel
Merke: Gegeben sind zwei parallele Geraden, die von
einer dritten geschnitten werden.
Die Winkel α und β sind Stufenwinkel.
α
β
Stufenwinkelsatz: Stufenwinkel an geschnittenen
Parallelen sind gleich groß.
Übungen
LB. S. 153 Nr.2 mündlich
154 Nr.3 Berechnungen
Übung interaktiv
Wechselwinkel
Merke: Gegeben sind zwei parallele Geraden, die von
einer dritten Geraden geschnitten werden.
Die Winkel γ und δ sind Wechselwinkel.
Wechselwinkelsatz: Wechselwinkel an geschnittenen
Parallelen sind gleich groß.
γ
δ
Dreiecke
Bezeichnungen am Dreieck
C
Eckpunkte: Große Buchstaben
γ
b
links unten beginnend entgegengesetzt dem Uhrzeigersinn
a
Seiten: kleine Buchstaben
Seiten gegenüber dem gleichnamigen Eckpunkt
α
A
 Winkel: Griechische Buchstaben
β
c
B
Zeichne drei verschieden Dreiecke. Beschrifte die Innenwinkel und bestimme
Ihre Größe.
Innenwinkelsatz
Die Summe der Innenwinkel eines Dreiecks beträgt 180°.
Übungen
LB.S. 157 Nr. 2, 4
S. 158 Nr. 6 ,10
α + β + γ = 180°
Interaktive Übung
1. Einteilung der Dreiecke nach Winkeln
Spitzwinklige Dreiecke
Alle Winkel sind spitz.
Rechtwinklige Dreiecke
Stumpfwinklige Dreiecke
Ein Winkel ist ein rechter W.
Ein Winkel ist stumpf.
2. Einteilung der Dreiecke nach Seiten
Unregelmäßige Dreiecke
Gleichschenklige Dreiecke
Gleichseitige Dreiecke
Alle Seiten sind
verschieden lang.
Zwei Seiten sind gleich
lang.
Alle Seiten sind gleich
lang.
Gleichschenklige Dreiecke
Winkel in der Spitze
C
b
a
Schenkel
Basiswinkel
A
c
Basis
B
Symmetrieachse
Übungen
LB.S. 162 Nr.6, 7
10
Bei einem gleichschenkligen Dreieck sind
zwei Seiten gleich lang.
Die beiden gleichlangen Seiten heißen
Schenkel, die dritte Seite heißt Basis.
Die der Basis anliegenden Winkel heißen
Basiswinkel.
Die beiden Basiswinkel sind gleich groß.
Dreiecksquiz
Gleichseitige Dreiecke
C
b
A
In einem gleichseitigen Dreieck sind alle
Seiten gleich lang.
Alle Winkel sind gleich groß.
Es gibt drei Symmetrieachsen.
a
c
B
Übung LB.S.163 Nr.8