1.1 Die Methoden der Wirtschaftswissenschaften

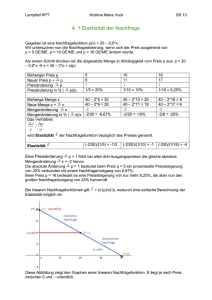
Gabriele Hildmann
Volkswirtschaftslehre WS 2011/12
Aufgabenblatt 3
Die Nutzenfunktion einer Studentin im Hinblick auf die Güter 1 und 2 lässt sich wie folgt beschreiben: U = x10 ,65 * x20 ,35 . Die Studentin verfügt über ein Budget von 500 €, das sie für den
Erwerb der beiden Güter 1 und 2 wenden will. Gut x1 kostet 8,- € und Gut 2 kostet 12,1. Siehe Excel-Datei
2. L = x10 ,65 * x20 ,35 + λ * (500 − 8 x1 − 12 x2 )
∂L
= 0,65 * x1−0 ,35 * x20 ,35 − 8λ = 0
∂x1
∂L
= 0,35 * x10 ,65 * x2−0 ,65 − 12λ = 0
∂x2
∂L
= 500 − 8 x1 − 12x2 = 0
∂λ
0,65 * x1−0 ,35 * x20 ,35
0,35 * x10 ,65 * x2−0 ,65
0,65 * x2
0,35 * x1
0,65x2 =
=
=
8λ
12λ
8
12
8
* 0,35 * x1
12
2,7857x2 = x1
500 − 8 * 2,7857x2 − 12 x2 = 0
500 = 34 ,2856 x2
14 ,5833 = x2
2,7857 * 14 ,5833 = x1 = 40,6250
Graphik siehe Excel-Datei
3. Siehe Excel-Datei.
4. Siehe Excel-Datei.
5. Siehe Excel-Datei.
6. Siehe Excel-Datei. Bitte beachten: E=500 (alles bezieht sich auf die Ausgangssituation).
7. Gleiche Frage wie unter 6)
8. Gehen Sie von folgender Nachfragefunktion aus: 100-5p. Bestimmen Sie die Preiselastizität der Nachfrage bei einem Preis von 10,- €. Bestimmen Sie die Preiselastizität der Nachfrage bei einem Preis von 15,- €. Interpretieren Sie das Ergebnis und erklären Sie die Unterschiede.
Nachfragefunktion:
x = 100 − 5p
Preis = 10:
x = 100 − 5 * 10 = 50
1%-Preiserhöhung (Preis = 10,10)
x = 100 − 5 * 10,1 = 49,5
Durch die Preiserhöhung um 1 Prozent (von 10,00 € auf 10,10 €) geht die Menge um 0,5
Einheiten auf 49,5 Einheiten zurück. Bezogen auf die Menge vor der Preiserhöhung (50
Stück) entspricht dies einem Rückgang von 1%. Als Elastizität ergibt sich damit -0,01/0,01
= -1. Die Elastizität von -1 besagt, dass (ausgehend von einem Preis von 10 €) eine 1prozentige Erhöhung des Preises zu einem Rückgang der Absatzmenge um 1 Prozent führen wird.
Preis = 15:
x = 100 − 5 * 15 = 25
1%-Preiserhöhung (Preis = 15,15)
x = 100 − 5 * 15,15 = 24 ,25
Durch die Preiserhöhung um 1 Prozent geht die Menge um 0,75 Einheiten auf 24,25 Einheiten zurück. Bezogen auf die Menge vor der Preiserhöhung (25 Stück) entspricht dies
einem Rückgang von 3%. Als Elastizität ergibt sich damit -0,03/0,01 = -3. Die Elastizität
von -3 besagt, dass (ausgehend von einem Preis von 15 €) eine 1-prozentige Erhöhung
des Preises zu einem Rückgang der Absatzmenge um das Dreifache der relativen Preisänderung führen wird.
Zwar verläuft die eigentliche Nachfragefunktion in diesem Beispiel linear, dies bedeutet
inhaltlich jedoch nur, dass eine Änderung des Preises um einen gleichen absoluten Betrag einen konstanten absoluten Rückgang der Menge verursacht. Die Elastizität beantwortet dagegen die Frage, wie sich eine relative Änderung des Preises auf die relative
Änderung der Menge auswirkt. Die absoluten Preisänderungen bei einer Preiserhöhung
um 1 Prozent, sind bei einem Preis von 15 € natürlich größer als bei einem Preis von 10 €,
bei einer linearen Funktion muss dies zu unterschiedlichen Mengenreaktionen führen.
2
9. Der Zusammenhang zwischen dem Preis eines Gutes und der nachgefragten Menge wird
in der Konsumfunktion (= Nachfragefunktion eines einzelnen Haushalts) dargestellt.
Zur Bestimmung der individuellen Nachfragefunktion müssen die Nachfragemengen des
Haushalts bei unterschiedlichen Preisen des Gutes ermittelt werden. Es wird dabei unterstellt, dass die Nutzenfunktion des Haushaltes, das Einkommen und der Preis des anderen Gutes konstant bleiben. Dadurch wird sichergestellt, dass Änderungen der Menge
allein auf die Veränderung des Preises des Gutes zurückzuführen sind.
Bekanntlich bewirkt eine Preisänderung eines Gutes (bei konstantem Einkommen und
unveränderten Preises des anderen Gutes) eine Drehung der Budgetlinie, deren Lage natürlich auch vom Einkommen und dem Preis des anderen Gutes beeinflusst wird. Durch
eine Preisänderung verschieben sich die relativen Preise und damit auch die Steigung der
Budgetlinie.
Die Nutzenfunktion des Haushaltes wird über die Indifferenzkurve abgebildet. Sie zeigt
alle Gütermengenkombinationen, die dem Haushalt den gleichen Nutzen stiften.
Am Tangentialpunkt zwischen Budgetlinie und Indifferenzkurve befindet sich das Haushaltsoptimum. Das Haushaltsoptimum ist diejenige Gütermengenkombination, die dem
Haushalt bei gegebener Nutzenfunktion, gegebenem Einkommen und gegebenen Preisen den höchsten Nutzen stiftet. Aufgrund der Rationalitätsannahme ist der Haushalt bestrebt diese Güterkombination zu realisieren.
Indem nun in Abhängigkeit vom Preis des Gutes die jeweiligen Budgetkinien und Tangentialpunkte (also die Haushaltsoptima) bestimmt werden, ergibt sich die Preis-KonsumKurve. Sie stellt den Zusammenhang zwischen der Nachfrage nach den beiden Gütern
und der Preisänderung eines Gutes herstellt. Damit gibt sie indirekt auch den Zusammenhang zwischen dem Preis eines Gutes und seiner nachgefragten Menge wieder, denn
werden die Preise und die entsprechenden Mengen in ein Preis-Mengen-Diagramm
übertragen, so ergibt sich die Preisabsatzkurve, das heißt die Nachfragekurve des Haushalts.
x2
Preis-Konsum-Kurve
p2
x1
Dies ist allerdings nicht die typische Darstellungsform einer Nachfragekurve. Sie ergibt
sich, wenn der Preis auf der waagerechten und die Menge auf der senkrechten Achse
abgetragen werden.
3
p2
Preisabsatzkurve
= Nachfragekurve
x2
4