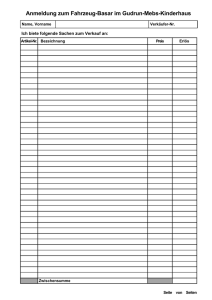
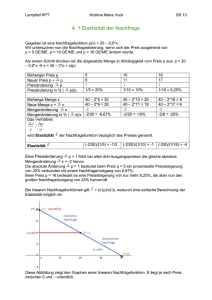
E(x) - Hu-berlin.de

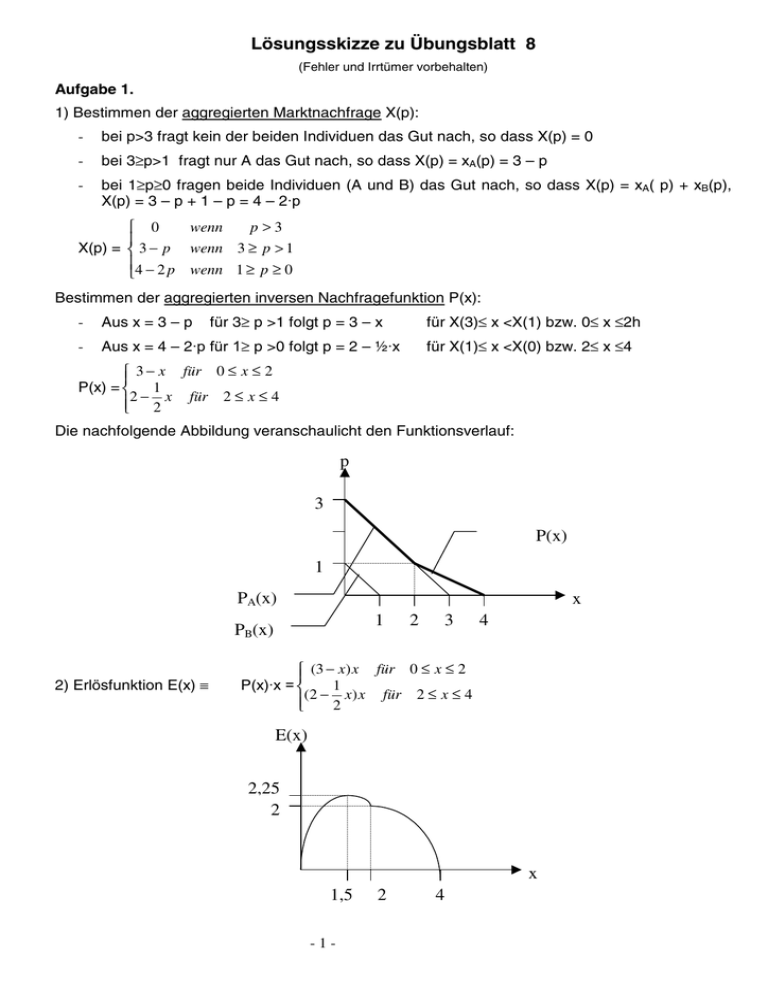
Lösungsskizze zu Übungsblatt 8
(Fehler und Irrtümer vorbehalten)
Aufgabe 1.
1) Bestimmen der aggregierten Marktnachfrage X(p):
-
bei p>3 fragt kein der beiden Individuen das Gut nach, so dass X(p) = 0
-
bei 3≥p>1 fragt nur A das Gut nach, so dass X(p) = xA(p) = 3 – p
-
bei 1≥p≥0 fragen beide Individuen (A und B) das Gut nach, so dass X(p) = xA( p) + xB(p),
X(p) = 3 – p + 1 – p = 4 – 2ÂS
wenn
p>3
 0

X(p) =  3 − p wenn 3 ≥ p > 1
4 − 2 p wenn 1 ≥ p ≥ 0

Bestimmen der aggregierten inversen Nachfragefunktion P(x):
-
Aus x = 3 – p
-
Aus x = 4 – 2ÂSIU≥ p >0 folgt p = 2 – ½Â[
für X(3)≤ x <X(1) bzw. 0≤ x ≤2h
für 3≥ p >1 folgt p = 3 – x
für X(1)≤ x <X(0) bzw. 2≤ x ≤4
 3 − x für 0 ≤ x ≤ 2
P(x) = 
1
2 − 2 x für 2 ≤ x ≤ 4
Die nachfolgende Abbildung veranschaulicht den Funktionsverlauf:
p
3
P(x)
1
PA(x)
x
1
PB(x)
2) Erlösfunktion E(x) ≡
2
3
4
 (3 − x) x für 0 ≤ x ≤ 2
P(x)Â[ 
1
(2 − 2 x) x für 2 ≤ x ≤ 4
E(x)
2,25
2
x
1,5
-1-
2
4
3) Grenzerlösfunktion
3 − 2 x für 0 < x < 2
[In Grenzpunkten (z.B. x=2) unbestimmt!]
dE(x)/dx = 
 2 − x für 2 < x < 4
dE(x)/dx
3
2
4
x
1,5
-1
-2
Zu den Kandidaten für das Maximum einer Funktion F(x) gehören neben den Rändern bzw.
Grenzpunkten der Funktion auch die Punkte im inneren Bereich, für die gilt: dF(x)/dx = 0. Diese
Bedingung ist für die Erlösfunktion E(x) für folgende Werte von x erfüllt:
dE(x)/dx = 0 :
3 – 2x = 0 ⇔ x = 1,5 ∈(0,2)
2 – x = 0 ⇔ x = 2∉(2,4) [ 2 gehört nicht zum Definitionsbereich der Grenzerlösfunktion]
Wir haben also insgesamt 4 Kandidaten für das Maximum der Erlösfunktion:
x=0
der linke Rand des Definitionsbereiches
:
E(0) = (3 – 0)⋅0 = 0
x = 1,5
für diesen Punkt gilt dE(x)/dx = 0, siehe oben
:
E(1,5) = (3 - 1,5)⋅1,5 = 2,25
x=2
der mittlere Grenzwert des Definitionsbereiches:
E(2) = (3 – 2)⋅2 = 2
x=4
der rechte Rand des Definitionsbereiches
E(4) = (2 – ½ ⋅ 4)⋅4 = 0
:
Der Erlös wird also bei der Menge x*=1,5 maximal( siehe Abbildung oben).
Der Marktpreis ist dann gleich p*= 3 – 1,5 = 1,5
AUFGABE 2.
Da die Beförderungskosten für Briefe ( im relevanten Bereich) von der Menge unabhängig sind,
sind die Einnahmen ( der Erlös) bei der Diskussion einer Preiserhöhung die relevante Zielfunktion.
Wenn man die folgende Definition für den Erlös, E(p) = pÂ;S YHUZendet, so erhält man
unmittelbar:
 dX ( p) p 
dE ( p)
dX ( p)
= X ( p) + p
= X ( p) 1 +
 = X ( p)[1 + ε ( p)]
dp
dp
dp X ( p) 

dX ( p ) p
> - 1. Für
dp X ( p )
dX ( p )
p
p
die Nachfragefunktion X(p) = 10 – 2⋅p gilt:
= -2 und ε(p) = -2⋅
= . Die
dp
10 − 2 p
5− p
D.h. eine Preiserhöhung führt nur dann zu höheren Erlösen, wenn ε(p) =
-2-
Bedingung ε(p) > - 1 ist also genau dann erfüllt, wenn -
p
> - 1⇔ p< 5 – p ⇔ p < 2,5.
5− p
Zum gleichen Schluss kommt man auch ohne der Berechnung der Preiselastizität der Nachfrage:
E(p) = X(p)⋅p = (10 – 2⋅p)⋅p = 10⋅p – 2⋅p² und dE(p)/dp = 10 – 4p >0 ⇔ p < 2,5!
3
3
= − < - 1. Die Nachfrage ist also
5−3
2
elastisch, und eine Preiserhöhung führt zu geringeren Erlösen. Preise sollten gesenkt werden.
1. Ist in der Ausgangssituation p = 3, so gilt ε(3) = −
2. Ist in der Ausgangssituation p∈(0; 2,5), ist die Nachfrage unelastisch, ε(p) > - 1 (s.o.), und eine
Preiserhöhung führt zu höheren Erlösen. Preise sollten ( aus der Sicht der Post) erhöht werden.
3. Für die Nachfragefunktion X(p) = 100/p für p>0 gilt:
dX ( p)
= -100/p² und
dp
ε(p) = -⋅ −
100 p
⋅
= −1
p 2 100
p
D.h. Preiselastizität der Nachfrage ist für p>0 konstant. Ferner gilt für diese Nachfragefunktion,
dass für p>0 der Erlös konstant ist:
dE(p)/dp = X(p)[ 1 + ε(p)] = X(p)[ 1 – 1] = 0
Beachte, dass E(p) = X(p)⋅p = (100/p)⋅p = 100 für alle p>0 und E(0)=X(0)⋅0=0. Der Erlös ist also
bei allen positiven Preisen gleich hoch. Die Post kann also einen beliebigen positiven Preis
wählen, wenn sie ihre Erlöse maximieren will.
Nimmt man nun an, dass die Kosten mit der Nachfragemenge steigen, und die Post ihren Gewinn
(Erlös minus Kosten) maximieren will, ist es für sie bei dieser hypothetischen Nachfragefunktion
optimal, den Preis möglichst hoch zu setzen. Das führt zwar dazu, dass die Nachfrage nahezu
Null beträgt, die Post nimmt aber trotzdem 100¼HLQZlKUHQGGLH.RVWHQPLQLPDOVLQG
AUFGABE 3.
Das folgende Diagramm bildet die Situation auf dem Butter-Markt ab. D(p) bezeichnet die
Nachfrage- und S(p) die Angebotsfunktion. p2 ist der Gleichgewichtspreis: S(p2) = D(p2).
P
D(p)
S(p)
p1
p2
q
Q1 =D(p1)
-3-
Q2 = q = D(p2)
System der Ausgleichszahlungen.
Angenommen, die Regierung legt den Zielpreis bei p1 > p2 fest. Die Differenz p1-p2 muss die
Regierung für jedes hergestellte (und auf dem Markt angebotene) Pfund Butter an die Molkereien
zahlen. Die Gesamtzahlungen aus der Staatskasse belaufen sich auf
(p1 – p2)Â42
Butter-Aufkäufe und Bildung der Butterberge
Die Regierung will den Marktpreis bis zur Höhe von p1 (Zielpreis) hochtreiben. Bei diesem Preis ist
die Nachfrage gleich Q1, während die Angebotsmenge Q2 beträgt. Die Regierung muss also die
Menge Q2-Q1 Pfund Butter aufkaufen und für jedes Pfund den Preis p1 zahlen. Die Kosten, die
durch diese Maßnahme der Regierung entstehen, sind gleich
(Q2-Q1)ÂS1
Vergleich der Subventionsprogramme
Wenn die Kosten des Subventionsprogramms als Entscheidungskriterium herangezogen werden,
ist das Aufkauf-Programm genau dann vorzuziehen, wenn gilt:
(Q 2 - Q 1)ÂS1 < (p1 – p2)Â42 ⇔ Q 1ÂS1 > p2Â42 ⇔ p1⋅D(p1) > p2⋅D(p2)
Wie sich D(p)⋅p verändert, wenn der Preis von p2 auf p1 steigt, lässt sich mit Hilfe der folgenden
Formel aus der Aufgabe 2 ausdrücken:
 dD( p) p 
dD( p)
d
= D( p) 1 +
= D( p)[1 + ε ( p)] = D( p)[1 − ε ( p) ]
pD( p) = D( p) + p
dp D( p) 
dp
dp

Ist |ε(p)| <1 für alle p∈[p2, p1], so steigt das Produkt p⋅D(p) in diesem Preisbereich, wenn der Preis
p steigt. Es gilt also: p1⋅D(p1) > p2⋅D(p2).
Das Butteraufkauf-Programm ist also für die Regierung genau dann billiger, wenn die Nachfrage
im relevanten Preisbereich unelastisch ist.
-4-