Satz des Pythagoras

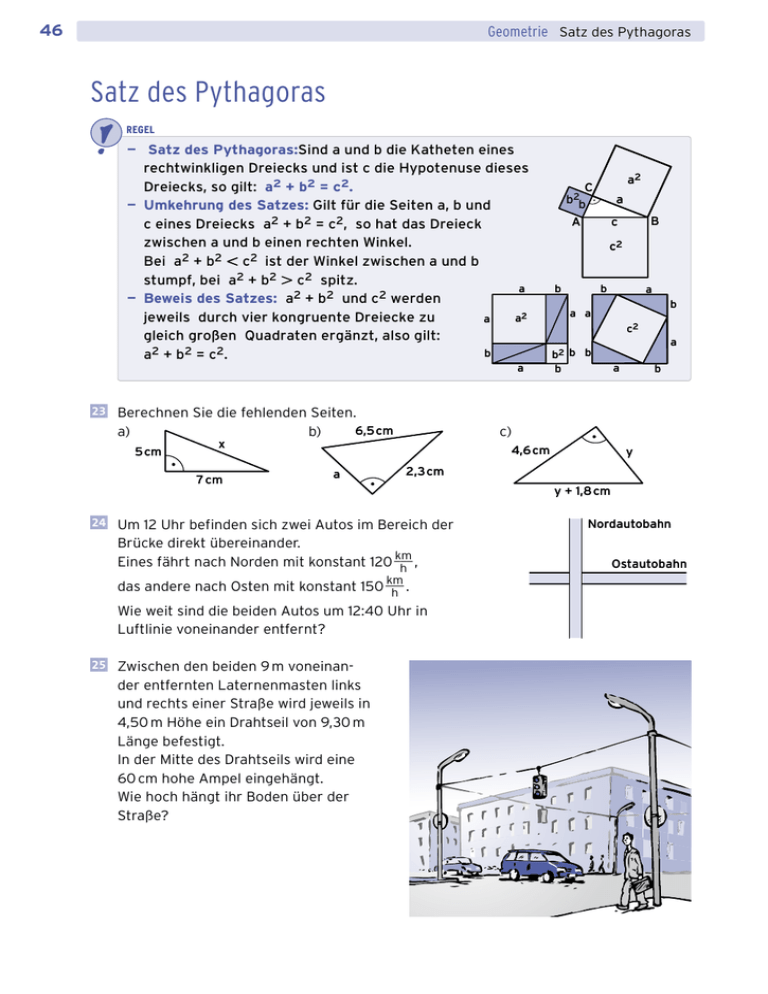
46
Geometrie Satz des Pythagoras
Satz des Pythagoras
REGEL
— Satz des Pythagoras:Sind a und b die Katheten eines
rechtwinkligen Dreiecks und ist c die Hypotenuse dieses
Dreiecks, so gilt: a2 + b2 = c2.
— Umkehrung des Satzes: Gilt für die Seiten a, b und
c eines Dreiecks a2 + b2 = c2, so hat das Dreieck
zwischen a und b einen rechten Winkel.
Bei a2 + b2 , c2 ist der Winkel zwischen a und b
stumpf, bei a2 + b2 . c2 spitz.
a
— Beweis des Satzes: a2 + b2 und c2 werden
jeweils durch vier kongruente Dreiecke zu
a2
a
gleich großen Quadraten ergänzt, also gilt:
b
a2 + b2 = c2.
a
<23< Berechnen Sie die fehlenden Seiten.
a)
b) 6,5cm
x
5cm
7cm
a
B
c
A
c2
b
b
a
b
a a
c2
b2 b b
b
4,6 cm
a
a
b
y
2,3 cm
Brücke direkt übereinander.
km
​ ,
Eines fährt nach Norden mit konstant 120 ​ ___
h
km
das andere nach Osten mit konstant 150 ​ ___
​ .
h
Wie weit sind die beiden Autos um 12:40 Uhr in
Luftlinie voneinander entfernt?
der entfernten Laternenmasten links
und rechts einer Straße wird jeweils in
4,50 m Höhe ein Drahtseil von 9,30 m
Länge befestigt.
In der Mitte des Drahtseils wird eine
60 cm hohe Ampel eingehängt.
Wie hoch hängt ihr Boden über der
Straße?
a
c)
<24< Um 12 Uhr befinden sich zwei Autos im Bereich der
<25< Zwischen den beiden 9 m voneinan-
a2
C
b2b
y + 1,8 cm
Nordautobahn
Ostautobahn
47
Geometrie Kathetensatz und Höhensatz
Kathetensatz und Höhensatz
REGEL
— Kathetensatz: Im rechtwinkligen Dreieck ist
das Quadrat über einer Kathete inhaltsgleich
zu dem Rechteck aus der gesamten Hypotenuse und dem der Kathete anliegenden Hypotenusenabschnitt.
a2 = c · p; b2 = c · q
a2
C
b2 b
a
c·q
A q
— Höhensatz: Im rechtwinkligen Dreieck ist das
Quadrat über der Höhe auf die Hypotenuse inhaltsgleich mit dem Rechteck aus den beiden
­Hypotenusenabschnitten, die von dieser Höhe
erzeugt werden.
h2 = p · q
— Beweis des Höhensatzes:
h2 = b2 — q2 (Satz des Pythagoras)
h2 = c · q — q2(Kathetensatz)
h2 = q · (c — q)(q ausgeklammert)
h2 = q · p
(c — q = p)
c
p
B
c·p
C
h2
h
q
A
p
B
p·q
<26< Gegeben ist das abgebildete Rechteck.
Konstruieren Sie mithilfe des Kathetensatzes ein inhaltsgleiches Quadrat.
Hinweis: Fassen Sie a als Hypotenuse und
b als an­liegenden Hypotenusenabschnitt
auf.
Die Konstruktion ist bereits begonnen,
setzen Sie sie fort.
A
H
B
b
a
<27< Gegeben sind das abgebildete Quadrat
___
und die abgebildete Strecke AB​
​ . Konstruieren Sie mithilfe des Höhensatzes ein Rechteck, das denselben
Flächen­inhalt wie das Quadrat___
hat und
dessen eine Seite die Strecke AB​
​ ist.
Die Konstruktion ist bereits begonnen.
a
C
a
A
B