Arbeitsblätter - ftb
Werbung

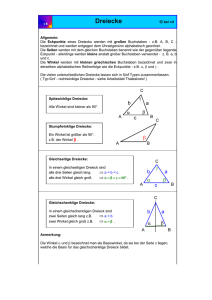
GIBZ Gewerblich-industrielles Bildungszentrum ZUG 1 KON1/PME1/AU1 Geometrie Geometrie, Definition Das Wort Geometrie stammt aus dem Griechischen und bedeutet so viel wie „Landmass“. Schon seit der Antike wird die Geometrie, die Landvermessung eingesetzt um die Besitzverhältnisse der Grundeigentümer genau festzulegen. Auch der Bau der Pyramiden vor ca. 4000 Jahren war nicht möglich, ohne „präzise“ Vermessungsmethoden und Berechnungen der Grössenverhältnisse. So hat sich die Geometrie im Lauf der Jahre zu einer Wissenschaft entwickelt, welche als Teilgebiet der Mathematik gilt. Die Geometrie beschäftigt sich mit Punkten, Geraden, Ebenen. Die kürzeste Distanz zwischen 2 Punkten ist die Gerade. Aus Gründen der Uebersichtlichkeit wird der Punkt hier deutlich sichtbar dargestellt, in der Geometrie gilt jedoch, dass der Punkt unendlich klein ist und keine Fläche besitzt. Fügt man drei Geraden zusammen, entsteht ein Dreieck Jede Ecke wird mit einem Grossbuchstaben gekennzeichnet, so heisst dieses Dreieck ABC Kap. 1: Dreiecke, Vierecke, Polygone Seite 1 GIBZ Gewerblich-industrielles Bildungszentrum ZUG KON1/PME1/AU1 Geometrie Die Seiten eines Dreiecks werden mit Kleinbuchstaben gekennzeichnet. Der Winkel links unten könnte man bezeichnen als Winkel CAB oder Winkel BAC, einfacher ist es jedoch den Winkeln einen griechischen Buchstaben zuzuweisen. 2. Dreiecksarten Ungleichmässige Dreiecke Die Seiten a, b und c weisen alle eine unterschiedliche Länge auf, demzufolge sind winkel und unterschiedlich gross Gleichschenkelige Dreiecke: Zwei der 3 Seiten (Schenkel, hier a und b) sind gleich gross, demzufolge sind die angrenzenden Winkel und gleich gross. Kap. 1: Dreiecke, Vierecke, Polygone Seite 2 GIBZ Gewerblich-industrielles Bildungszentrum ZUG KON1/PME1/AU1 Geometrie Gleichseitige Dreiecke: Die 3 Seiten des Dreiecks sind alle gleich gross, demzufolge sind alle Winkel ebenfalls gleich gross. Weil die Summe aller Winkel im Dreieck 360° beträgt, gilt = = = 60° Rechtwinklige Dreiecke: In einem rechtwinkligen Dreieck ist einer der 3 Winkel (, oder ) 90° gross. Dieser Winkel wird mit einem Bogen und Punkt gekennzeichnet. Die Summe der verbleibenden Winkel ist deshalb 90°, diese können, müssen aber nicht gleich gross sein. Unmögliche Dreiecke: Ein unmögliches Dreieck ist das Penrose-Dreieck,auch Tribar genannt. Hierbei handelt es sich um eine optische Täuschung, dieses Dreieck kann in Wirklichkeit nicht gebaut werden, dennoch gilt es Konstruktionen, die ein solches Dreieck vortäuschen. Nur wenn diese Konstruktionen aus einer Richtung (und nur dieser Richtung) betrachtet werden, sehen sie wie ein Tribar aus. Sieht aus wie ein Dreieck... Kap. 1: Dreiecke, Vierecke, Polygone ... ist es aber nicht. Seite 3 GIBZ Gewerblich-industrielles Bildungszentrum ZUG 3. KON1/PME1/AU1 Geometrie Vierecke Wie bei den Dreiecken, ist bei den Vierecken auch die unregelmässige Form anzutreffen, bei welcher keiner der Seiten die gleiche Grösse hat wie die andere. Dennoch gibt es einige spezielle Formen des Vierecks, die besondere Beachtung bedürfen: Das Rechteck In einem Rechteck befinden sich nur rechte Winkel, d.h. alle Winkel sind 90° gross. Die Summe aller Winkel* beträgt somit 360°. Im Rechteck sind die sich gegenüber liegende Seiten immer gleich lang. Das Quadrat Das Quadrat ist eine Sonderform des Rechtsecks, wobei nicht nur alle Winkel 90° gross, sondern auch alle Seiten gleich lang sind. Das Parallelogramm: Parallel heisst „in die gleiche Richtung verlaufend“, in einem Parallelogramm verlaufen die sich gegenüberliegende Seiten in die gleiche Richtung, sind also parallel. Das Trapez: Kennzeichnend für ein Trapez ist, dass 2 seiner Seiten parallel, jedoch nicht gleich lang sind. *) Teilt man das Rechteck indem man von A nach C eine Diagonale zieht, entstehen 2 Dreiecke, die Summe der Winkel im Dreieck beträgt somit 180°. Kap. 1: Dreiecke, Vierecke, Polygone Seite 4 GIBZ Gewerblich-industrielles Bildungszentrum ZUG 4. KON1/PME1/AU1 Geometrie Polygone „Poly“ kommt aus dem Griechischen und bedeutet „viel“. ein Polygon ist also ein Vieleck mit mindestens 5 Seiten und Winkeln (sonst würde man von Drei- oder Viereck reden). Sowohl Winkel als auch Seitenlängen sind in der Regel unterschiedlich. Sonderformen sind die regelmässigenFünf-, Sechs- , usw. Ecken, die aus 5, bzw. 6 gleich langen Seiten aufgebaut sind. Unregelmässiges Sechseck: Regelmässiges Sechseck Hausaufgaben: 1. Zeichnen Sie: - ein gleichschenkliges Dreieck - ein Rechteck - ein regelmässiges Hexagon (6-Eck) 2. Im Dreieck ABC sind die Seiten AB und BC gleich lang. Welche Winkel sind gleich gross? a) Winkel ABC und BCA b) Winkel BCA und CAB c) Winkel CAB und ABC 3. Worin besteht der Unterschied zwischen einem Quadrat und ein Rechteck? 4. In einem rechtwinkligen Dreieck ist Winkel CAB = 90° und Winkel ABC = 45°. Wie gross ist Winkel ACB? Als was könnte man dieses Dreieck auch bezeichnen? 5. Was ist eine Diagonale? Kap. 1: Dreiecke, Vierecke, Polygone Seite 5