Lösungshinweise zu den Übungsaufgaben Inhalt

Lösungshinweise zu den Übungsaufgaben
Inhalt
Kapitel 2 ................................................................................................................. 2
Kapitel 3 ............................................................................................................... 11
Kapitel 4 ............................................................................................................... 25
Kapitel 5 ............................................................................................................... 34
Kapitel 2
Aufgabe 2.1: Mindestpreis
In einem Wettbewerbsmarkt sei die Nachfragefunktion mit 𝑄 𝐷 (𝑃) =
12 − 𝑃 gegeben. Die Angebotsfunktion der Unternehmen sei 𝑄 𝑆 (𝑃) =
2𝑃.
a)
Stellen Sie die inverse Nachfrage- und Angebotsfunktion
graphisch dar und berechnen Sie die gleichgewichtige Marktallokation.
Im Gleichgewicht muss Nachfrage gleich Angebot sein:
𝑄 𝐷 (𝑃) = 𝑄 𝑆 (𝑃) ⟺ 12 − 𝑃 = 2𝑃 ⟺ 12 = 3𝑃
⟺ 𝑃∗ = 4 und 𝑄 ∗ = 8
⟺ Marktgleichgewicht im Punkt 𝐸
𝑃
8
𝐸‘
𝑃𝑚𝑖𝑛 6
𝐶
𝑃
∗
∆𝑄 = 6
𝐴
4
𝐸
𝐵
inverse
Nachfragefunktion 𝑄𝐷
2
0
b)
inverse
Angebotsfunktion 𝑄 𝑆
2
4
6
8
𝑄∗
10
12
𝑄
Berechnen Sie Konsumenten- und Produzentenrente sowie die
soziale Wohlfahrt im Gleichgewicht.
KR = ½ ∙ 8 ∙ (12 − 4) = 32 und PR = ½ ∙ 8 ∙ 4 = 16
Gesamtwohlfahrt = 𝑊 = KR + PR = 48
c)
Die Regierung setzt einen Mindestpreis 𝑃𝑚𝑖𝑛 = 6, um die
Anbieter des Gutes besser zu stellen als in der Marktlösung. Wie
2
hoch ist das Überschussangebot? Stellen Sie die Situation graphisch dar.
𝑄 𝑆 (𝑃𝑚𝑖𝑛 ) = 12 und 𝑄 𝐷 (𝑃𝑚𝑖𝑛 ) = 6 => Überschussangebot von 𝑄 = 6
⟺ neues Marktgleichgewicht im Punkt 𝐸′ (vgl. Abb.)
d)
Welche Auswirkungen hat der Mindestpreis auf die Renten für
beide Marktseiten? Berechnen Sie wie in b) die Renten und die
soziale Wohlfahrt.
Konsumenten verlieren 𝐶 und 𝐴: ∆𝐾𝑅 = −𝐶 − 𝐴 < 0
Produzenten gewinnen 𝐶 und verlieren 𝐵: ∆𝑃𝑅 = 𝐶 − 𝐵 > 0
Wirkung auf die Gesamtwohlfahrt:
∆𝑊 = ∆𝐾𝑅 + ∆𝑃𝑅 = −𝐶 − 𝐴 + 𝐶 − 𝐵 = −𝐴 − 𝐵 < 0
Renten in der neuen Situation mit Mindestpreis:
𝐾𝑅 ′ = ½ ∙ 6 ∙ 6 = 18
𝑃𝑅 ′ = ½ ∙ 3 ∙ 6 + 3 ∙ 6 = 27
𝑊′ = 45
∆𝑊 = 𝑊 ′ − 𝑊 = 45 – 48 = −3
e)
Was passiert, wenn die Regierung den Mindestpreis 𝑃𝑚𝑖𝑛 = 3
setzt?
Es passiert nichts, da der Mindestpreise nicht „bindet“, d.h. keine
Wirkung entfaltet. Käufer und Produzenten handeln ohne Mitwirken
des Staates zu einem höheren Marktpreis (vgl. Abb.).
Aufgabe 2.2: Elastizität
a)
Bestimmen Sie für die Marktallokation aus Aufgabe 2.1a) die
Preiselastizität der Nachfrage und des Angebots. Interpretieren
Sie diese Werte.
Preiselastizität der Nachfrage:
Hier:
∆𝑄 𝐷
𝐸𝑃𝐷
=
∆𝑄𝐷
𝑄𝐷
∆𝑃
𝑃
=
∆𝑄 𝐷 𝑃
∆𝑃 𝑄 𝐷
4
1
𝑄 𝐷 (𝑃) = 12 − 𝑃 ⟹ ∆𝑃 = −1 ⟹ 𝐸𝑃𝐷 (𝑃 = 4, 𝑄 = 8) = −1 8 = − 2
Interpretation: Eine 1%ige Preiserhöhung führt zu einer Nachfragereduktion um 0,5%. |𝐸𝑃𝐷 | < 1, also ist die Preiselastizität der Nachfrage
3
unelastisch: Die relative Mengenänderung ist kleiner als die
ursächliche relative Preisänderung.
Preiselastizität des Angebots: 𝐸𝑃𝑆 =
Hier: 𝑄 𝑆 (𝑃) = 2𝑃 ⟹
∆𝑄 𝑆
∆𝑃
∆𝑄𝑆
𝑄𝑆
∆𝑃
𝑃
=
∆𝑄 𝑆 𝑃
∆𝑃 𝑄 𝑆
4
= 2 ⟹ 𝐸𝑃𝑆 (𝑃 = 4, 𝑄 = 8) = 2 8 = 1
Interpretation: Eine 1%ige Preiserhöhung führt zu einer Angebotserhöhung um 1%. |𝐸𝑃𝑆 | = 1, also ist die Preiselastizität des Angebots
einheitselastisch: Die relative Mengenänderung ist gleich der
ursächlichen relativen Preisänderung.
Der Vergleich der Beträge beider Elastizitäten zeigt, dass die
Nachfrage in geringerem Maße auf Preisänderungen reagiert als das
Angebot, also ist die Nachfrage unelastischer als das Angebot.
b)
Wie müsste man die inverse Nachfragekurve drehen, damit die
Preiselastizität in einem beliebigen Punkt kleiner wird?
Im Uhrzeigersinn, die inverse Nachfrage 𝑄 𝐷 wird steiler.
Aufgabe 2.3: Mengensteuer
a)
Angenommen, in der Situation wie in Aufgabe 2.1a) führt der
Staat eine Mengensteuer 𝑡 = 2 ein, wobei die Angebotsseite die
Steuer an den Fiskus abführen muss. Berechnen Sie die neue
Marktallokation, die Zusatzlast der Besteuerung und das Steuervolumen. Stellen Sie das Problem graphisch dar.
4
𝑃
𝑄 𝑆 (𝑡)
8
𝐸𝐵
6
𝑃𝐵 (𝑡)
𝑃∗ 4
𝑃𝑁 (𝑡)
t
𝐴
𝐵
𝑄 𝑆 (0)
𝐶
𝐷
𝐸
𝐸𝑁
2
𝑄𝐷
t
0
2
4
6
8
𝑄(𝑡)
𝑄(0)
10
12
𝑄
Situation ohne Steuer:
Nachfrage: 𝑄 𝐷 (𝑃) = 12 − 𝑃
⟹ inverse Nachfrage: 𝑃(𝑄 𝐷 ) = 12 − 𝑄 𝐷 (In der Abb. mit 𝑄 𝐷
bezeichnet)
Angebot: 𝑄 𝑆 (𝑃) = 2𝑃
1
⟹ inverses Angebot: 𝑃(𝑄 𝑆 ) = 2 𝑄 𝑆 (In der Abb. mit 𝑄 𝑆 (0) bezeichnet)
Situation mit Steuer (vgl. Abb.):
Die Anbieter müssen die Steuer abführen und schlagen diese daher auf
ihren Nettopreis auf. Daher kommt es zu einer Verschiebung der
1
inversen Angebotskurve 𝑃(𝑄 𝑆 ) = 2 𝑄 𝑆 um 𝑡 = 2 nach oben zu
1
𝑃(𝑄 𝑆 ) = 2 𝑄 𝑆 + 2. Es ergibt sich somit die neue Angebotsfunktion
𝑄 𝑆 (𝑃𝐵 ) = 2𝑃𝐵 – 4.
Das neue Marktgleichgewicht liegt jetzt bei 𝐸𝐵 mit dem von den
Konsumenten zu zahlenden Bruttopreis 𝑃𝐵 > 𝑃∗ . Zu diesem Preis
fragen die Konsumenten die Menge 𝑄(𝑡) < 𝑄(0) nach. Da die
Produzenten jedoch nicht 𝑃𝐵 , sondern nur 𝑃𝑁 = 𝑃𝐵 − 𝑡, also den
Nettopreis ohne Steuern, erhalten, sind sie auch nur bereit, 𝑄(0) zu
verkaufen. Dadurch erhält man ein Nettopreis- und ein Bruttopreisgleichgewicht (𝐸𝐵 und 𝐸𝑁 ) bei der Menge 𝑄(𝑡).
5
Neues Marktgleichgewicht über Bruttopreis 𝑃𝐵 :
𝑄 𝐷 (𝑃𝐵 ) = 𝑄 𝑆 (𝑃𝐵 − 𝑡) ⟺ 12 − 𝑃𝐵 = 2𝑃𝐵 − 4 = ⟺ 3𝑃𝐵 = 16
⟺ 𝑃𝐵 = 5,33 und 𝑄(𝑡) = 6,67
Steuervolumen: 𝑡𝑄(𝑡) = 2 ∙ 6,67 = 13,33 = 𝐴 + 𝐵
Zusatzlast: ½(𝑄(0) − 𝑄(𝑡)) ∙ 𝑡 = 1,33 = 𝐶 + 𝐷
Nettopreis: 𝑃𝑁 = 𝑃𝐵 − 𝑡 = 5,33 − 2 = 3,33
b)
Welche der Marktseiten trägt mehr von der Steuerlast?
Begründung.
Da in Aufgabe 2.2 bereits gezeigt wurde, dass die Nachfrage
unelastischer als das Angebot ist, tragen die Konsumenten hier einen
größeren Anteil der Steuerlast. Es spielt keine Rolle, wer die Steuer
letztendlich an den Staat abgeben muss.
Ein Maß für die Verteilung der Steuerlast ist
∆𝑃𝐵
1,33
2
∆𝑃𝐵
∆𝑡
.
= 2 = 0,67 ⟺ 3 der Steuer wird von den Konsumenten
getragen. 𝐾𝑅 = −𝐴 − 𝐶
∆𝑃
1,33
1
1 − ∆𝑡𝐵 = 1 − 2 = 0,34 ⟺ 3 der Steuer wird von den Produzenten getragen. 𝑃𝑅 = −𝐵 − 𝐷
Die Wirkung auf die Gesamtwohlfahrt ist ∆𝑊 = −𝐶 − 𝐷. Als
Steuervolumen steht dem Staat 𝐴 + 𝐵 zur Verfügung steht.
∆𝑡
Aufgabe 2.4: Güter
a)
Nennen Sie drei Güterpaare, bei denen die Güter substitutiv
(komplementär) zueinander sind. Welches Vorzeichen hat die
Kreuzpreiselastizität der Nachfrage für diese Güterpaare?
Substitutive Güter: Butter und Margarine, Kalbfleisch und Rindfleisch, Theaterbesuch und Kinobesuch, Salzbrezeln und Salzstangen.
Komplementäre Güter: Benzin und Motoröl, Brief und Briefmarke,
Messer und Gabel, Hardware und Software, DVD-Player und DVD.
Die Kreuzpreiselastizität bei Substituten ist positiv (der Preis des
einen Gutes steigt, somit sinkt die Nachfrage nach diesem Gut und die
Nachfrage nach dem substitutiven Gut steigt).
6
Die Kreuzpreiselastizität bei komplementären Gütern ist negativ
(steigt der Preis des einen Gutes, geht die Nachfrage nach beiden
Gütern zurück).
Nennen Sie je drei unterschiedliche Güter, die relativ preiselastisch bzw. preisunelastisch nachgefragt werden (Hinweis:
Beachten Sie den Zeithorizont Ihrer Analyse). Begründung.
b)
Relativ unelastisch: lebensnotwendige Güter, z.B. Wasser, Brot,
lebensnotwendige Medizin. Verbrauchsgüter wie Benzin oder
Elektrizität in der kurzen Frist.
Relativ elastisch: Verbrauchsgüter wie Benzin und Elektrizität in der
langen Frist.
Aufgabe 2.5: Stromtarif
Jochen gilt als typischer Verbraucher von Elektrizität. Seine
Nachfrage nach Elektrizität wird durch die Gleichung 𝑄 𝐷 (𝑃) =
3000 − 100𝑃 angegeben, wobei 𝑄 𝐷 in Kilowattstunden (kWh) pro
Monat und 𝑃 in €Cent pro kWh gemessen wird.
a)
Berechnen Sie Jochens Preiselastizität der Nachfrage in den
Punkten 𝑃 = 20 und 𝑃 = 25.
𝑃 = 20 ⟺ 𝑄 𝐷 (𝑃) = 1000
∆𝑄 𝐷
∆𝑃
𝐸𝑃𝐷
= −100
=
∆𝑄 𝐷 𝑃
∆𝑃 𝑄 𝐷
20
= −100 ∙ 1000 = −2
𝑃 = 25 ⟺ 𝑄 𝐷 (𝑃) = 500
𝐸𝑃𝐷 =
b)
∆𝑄 𝐷 𝑃
∆𝑃 𝑄 𝐷
25
= −100 ∙ 500 = −5
Wenn die Grenzkosten der Produktion gleich Null wären und der
Preis gegenwärtig bei 𝑃 = 20 festgesetzt ist, würden Sie dem
lokalen Stromversorgungsunternehmen empfehlen, den Preis
anzuheben oder zu senken?
𝐸𝑃𝐷 = −2 entspricht einer elastischen Nachfrage, somit sollte der
Preis nicht angehoben werden, da die relative Mengenänderung größer
sein wird als die ursächliche relative Preisänderung. Mit anderen
7
Worten: Der Erlös sinkt, wenn der Preis steigt. Der Preis sollte
stattdessen gesenkt werden, denn dann steigt der Erlös.
Hinweis: Man kann zeigen, dass im Monopol Erlösmaximierung (=
Gewinnmaximierung, wenn 𝐺𝐾 = 0 und keine fixen Kosten)
äquivalent ist zu einer Marktallokation mit 𝐸𝑃𝐷 = −1.
c)
Angenommen, der lokale Stromversorger stellt für große
Mengen an monatlich verbrauchten kWh einen höheren Preis in
Rechnung, um so den Verbrauch einzuschränken und den Umweltschutz zu fördern. Darüber hinaus sei angenommen, für die
ersten 500 im Monat konsumierten kWh gilt 𝑃 = 10 und für alle
verbleibenden nachgefragten kWh gilt 𝑃 = 20. Wie hoch wäre
Jochens Konsumentenrente? Illustrieren Sie dies.
𝑃 𝑖𝑛 €𝐶𝑒𝑛𝑡
30
25
𝑄𝑆
20
15
10
5
𝑄𝐷
𝑄 𝑖𝑛 𝑇𝑘𝑊ℎ
0
0,5
1
1,5
2
2,5
3
𝐾𝑅 = ½ ∙ 1000 ∙ 10 + 500 ∙ 10 = 10.000€𝐶𝑒𝑛𝑡 = 100€
Vgl. grau markierte Fläche in der Abb.
Aufgabe 2.6: Benzinsteuer
In den USA wird die Einführung einer zusätzlichen Benzinsteuer
diskutiert. Im Folgenden wollen wir untersuchen, wie eine Steuer von
$0,50 pro Gallone den Preis und den Konsum von Benzin in den USA
8
beeinflussen würde. Gehen Sie von einem Gesamtverbrauch an Benzin
in den USA von 134 Mrd. Gallonen pro Jahr aus. Der Preis vor der
Einführung der Steuer sei $3,60 pro Gallone. Gehen Sie von einer
mittelfristigen Elastizität der Benzinnachfrage von −0,5 aus. Die
mittelfristige Elastizität des Benzinangebots sei 0,4.
a)
Bestimmen Sie aus den Angaben die lineare Nachfragekurve und
die lineare Angebotskurve.
𝑄 𝐷 = 𝑎 − 𝑏𝑃, 𝑄 𝑆 = 𝑐 + 𝑑𝑃
𝐸𝑃𝐷 =
∆𝑄 𝐷 𝑃
∆𝑃 𝑄 𝐷
𝑃
3,6
= −𝑏 𝑄 ⟺ −0,5 = −𝑏 134
⟺ 𝑏 = 18,61 𝑀𝑟𝑑. 𝐺𝑎𝑙𝑙𝑜𝑛𝑒𝑛
∆𝑄 𝑆 𝑃
𝑃
3,6
=𝑑
⟺ 0,4 = 𝑑
𝑆
∆𝑃 𝑄
𝑄
134
⟺ 𝑑 = 14,89 𝑀𝑟𝑑. 𝐺𝑎𝑙𝑙𝑜𝑛𝑒𝑛
𝐸𝑃𝑆 =
Daraus folgt:
𝑄 𝐷 = 𝑎 − 18,61𝑃 ⟺ 134 = 𝑎 − 18,61 ∙ 3,6
⟺ 𝑎 = 201 𝑀𝑟𝑑. 𝐺𝑎𝑙𝑙𝑜𝑛𝑒𝑛
𝑄 𝑆 = 𝑐 + 14,89𝑃 ⟺ 134 = 𝑐 + 14,89 ∙ 3,6
⟺ 𝑐 = 80,39 𝑀𝑟𝑑. 𝐺𝑎𝑙𝑙𝑜𝑛𝑒𝑛
Lineare Angebots- und Nachfragekurven:
𝑄 𝐷 (𝑃) = 201 − 18,61𝑃
𝑄 𝑆 (𝑃) = 80,39 + 14,89𝑃
b)
Bestimmen Sie Brutto- und Nettopreis nach Einführung der
Benzinsteuer in Höhe von $0,50. Wie viel Prozent der Steuer
zahlen die Nachfrager, wie viel Prozent zahlen die Anbieter?
𝑄 𝐷 = 201 − 18,61𝑃𝐵
𝑄 𝑆 = 80,39 + 14,89𝑃𝑁
𝑃𝐵 = 𝑃𝑁 + 0,50
Neues Marktgleichgewicht über Nettopreis 𝑃𝑁 :
201 − 18,61(𝑃𝑁 + 0,50) = 80,39 + 14,89𝑃𝑁
⟺ 𝑃𝑁 = 3,32 und 𝑃𝐵 = 3,82
9
Konsumenten tragen 𝑃𝐵 − 𝑃∗ = 3,82 − 3,6 = $0,22
Produzenten tragen 𝑃∗ − 𝑃𝑁 = 3,6 − 3,32 = $0,28
∆𝑃
0,22
Analog: ∆𝑡𝐵 = 0,5 = 0,44 ⟺ 44% der Steuer wird von den
Konsumenten getragen. 56% der Steuer wird von den Anbietern
getragen.
c)
Wie hoch sind das jährliche Steuervolumen und die jährliche
Zusatzlast der Besteuerung? Stellen Sie das Problem graphisch
dar.
Das Steuervolumen ist 𝑇 = 𝑄(𝑡)𝑡 = 130 ∙ 0,5 = 65 𝑀𝑟𝑑. $
𝑄(0)−𝑄(𝑡)
134−130
Die Zusatzlast ist 𝑍 = 𝑡
= 0,5 ∙
= 1 𝑀𝑟𝑑. $
2
2
𝑄(0)
𝑄(𝑡) 𝑄 𝑆 (𝑡)
𝑄 𝑆 (0)
𝑃
𝑃𝐵 (𝑡) 3,824
3,60
𝑃∗
𝑃𝑁 (𝑡) 3,32
𝐸𝐵
t
𝐸
3
𝐸𝑁
2
𝑄𝐷
1
0
20
40
60
80
100
160 𝑄 𝑖𝑛
120 130 140
134 𝑀𝑟𝑑. 𝐺𝑎𝑙𝑙𝑜𝑛𝑒𝑛
10
Kapitel 3
Aufgabe 3.1: Monopol
Aus der Süddeutschen Zeitung vom 28. Juni 2004:
Das Bundeskartellamt ist nach Darstellung seines Präsidenten Ulf Böge einem
Geflecht von bundesweiten und regionalen Preisabsprachen im deutschen
Papiergroßhandel auf die Spur gekommen, durch die den Endverbrauchern ein
Schaden von mehreren Millionen Euro entstanden sei. Bis auf ganz wenige
Ausnahmen seien alle namhaften Firmen der Branche unter den Kartellteilnehmern
zu finden, deren Namen der Behördenchef aber noch nicht preisgeben wollte. Böge
gab jedoch zu verstehen, dass nach Abschluss der noch laufenden Ermittlungen mit
Bußgeldern in zweistelliger Millionenhöhe zu rechnen ist.
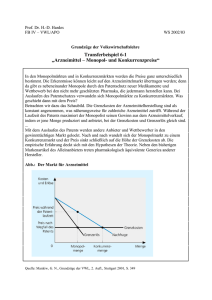
Erläutern Sie, warum das Vorgehen der Kartellbehörde aus gesamtwirtschaftlicher Sicht gerechtfertigt und wünschenswert ist. Gehen Sie
dazu in folgenden Schritten vor:
a)
Gehen Sie davon aus, dass die Kartellbildung der beteiligten
Unternehmen mit dem Ziel erfolgte, am Markt Monopolpreise
durchzusetzen. Erläutern Sie und zeigen Sie grafisch die gewinnmaximierende Ausbringungsentscheidung im Monopol
(Ermittlung des Cournotschen Punktes). Machen Sie klar, warum der Cournotsche Punkt tatsächlich ein Gewinnmaximum
charakterisiert!
11
Allgemein ist das Maximum des Firmengewinns durch die
Übereinstimmung von Grenzerlösen und Grenzkosten charakterisiert.
Übersteigen nämlich die Grenzerlöse die Grenzkosten, so kann durch
die Ausweitung der Angebotsmenge der Unternehmensgewinn
gesteigert werden (die nächste ausgebrachte Einheit Output
erwirtschaftet einen positiven Grenzgewinn). Liegen die Grenzerlöse
hingegen unter den Grenzkosten, so erwirtschaftet die nächste Einheit
Output einen Grenzverlust und sollte daher nicht produziert werden.
Im Falle eines Monopolunternehmens entfällt die gesamte
Marktnachfrage auf lediglich einen Anbieter. Der sieht sich deshalb
nun mit einer fallenden Grenzerlösfunktion konfrontiert. Für den Fall
einer linearen Preisabsatzfunktion 𝑃(𝑄) = 𝑎 − 𝑏𝑄, 𝑎, 𝑏 > 0 zeigt man
leicht, dass die Grenzerlösfunktion, vom selben Achsenabschnitt
kommend, mit negativer und genau doppelter Steigung wie die
Preisabsatzfunktion verläuft, denn:
𝑅(𝑄) = (𝑎 − 𝑏𝑄)𝑄 ⇒ 𝑅 ′ = 𝑎 − 2𝑏𝑄,
wobei 𝑅 der Erlös und 𝑅‘ der Grenzerlös ist.
Grafisch erhält man:
ℎ
2
12
Die Monopollösung lässt sich ablesen aus dem Cournotschen Punkt,
also dem Schnittpunkt der Grenzerlös- mit der Grenzkostenfunktion.
Lotet man senkrecht nach unten, so erhält man die gewinnmaximale
Absatzmenge 𝑄 𝑀 , die sogenannte Monopolmenge. Lotet man
senkrecht nach oben und dann nach links, so kann man aus der
Preisabsatzfunktion den zugehörigen Monopolpreis 𝑃𝑀 ablesen.
Jede abweichende Menge kann kein Gewinnmaximum sein. Betrachten wir beispielsweise die geringere Menge 𝑄1 < 𝑄 𝑀 . Wie man der
folgenden Grafik entnehmen kann, kann der Unternehmensgewinn
gesteigert werden, wenn die Ausbringungsmenge, ausgehend von 𝑄1
sukzessive bis zu 𝑄 𝑀 erhöht wird, denn im Bereich dieser Outputeinheiten übersteigen die Grenzerlöse offenbar die Grenzkosten.
1
1
2
Steigert die Firma zunächst ihren Output von Null auf die Menge 𝑄1,
so kann sie einen Gewinnzuwachs in Höhe der Fläche A realisieren,
der sich einfach aus der Fläche unterhalb der Grenzerlösfunktion und
oberhalb der Grenzkostenfunktion ablesen lässt (die Fläche unter der
Grenzerlösfunktion misst die Erlösänderung, die Fläche unter der
Grenzkostenfunktion misst die Kostenänderung). Demzufolge lässt
sich eine weitere Gewinnzunahme, gemessen duch die Fläche B,
13
erzielen, wenn die Outputmenge von 𝑄1 auf 𝑄 𝑀 gesteigert wird. Eine
Ausweitung der Produktion über die Monopolmenge hinaus ist
natürlich nicht sinnvoll, da dann die Kosten der nächsten produzierten
Einheiten Output die erzielten Erlöse übersteigen.
b)
Erläutern Sie nun die Preisbildung bei vollkommener Konkurrenz. Nach welcher Regel trifft ein gewinnmaximierendes
Unternehmen im Wettbewerbsmarkt seine Ausbringungsentscheidung? Machen Sie sich klar und erläutern Sie, was man
unter Preisnehmerverhalten versteht.
Vollkommene Konkurrenz ist nur bei atomistischer Marktstruktur
möglich, d.h. im Markt befinden sich viele, sehr kleine Anbieter, die
allesamt über keine messbaren Marktanteile verfügen. Unter diesen
Bedingungen kann die einzelne Firma mit ihrer Ausbringungsentscheidung den Marktpreis nicht beeinflussen. Der Preis ist aus Sicht
der einzelnen Unternehmung ein gegebenes, unverrückbares Datum,
an den sie sich durch optimale Wahl ihrer Ausbringungsmenge
anpasst. Man spricht davon, dass die Unternehmen sich als Preisnehmer und Mengenanpasser verhalten. Auch bei vollkommener
Konkurrenz ist die gewinnmaximale Ausbringungsmenge durch die
Übereinstimmung von Grenzerlösen und Grenzkosten charakterisiert.
Allerdings ist nun der Grenzerlös identisch zum Marktpreis und damit
auch eine exogen gegebene Größe, den das einzelne Unternehmen,
anders als ein Monopolist, nicht beeinflussen kann. Deshalb konkretisiert sich die allgemeine Gewinnmaximierungsregel „Grenzerlös =
Grenzkosten“ zu der Forderung, dass die Grenzkosten der Produktion
mit dem herrschenden Marktpreis übereinstimmen müssen. Formal
muss also für ein Gewinnmaximum die Forderung 𝑝 = 𝐺𝐾(𝑞) erfüllt
sein. Grafisch ergibt sich die gewinnmaximale Ausbringungsmenge
des Unternehmens bei vollkommener Konkurrenz also aus dem
Schnittpunkt der steigenden, kurzfristigen Grenzkostenfunktion mit
dem horizontal verlaufenden, gegebenen Marktpreis:
14
∗
Ausgehend von der Menge q können durch Steigerung der Ausbringungsmenge zusätzliche positive Grenzgewinne erwirtschaftet
werden, da bis zur Menge 𝑞 ∗ der Grenzerlös die Grenzkosten der
Produktion übersteigt.
c)
Ermitteln Sie grafisch den gesamtwirtschaftlichen Wohlfahrtsverlust, der sich aus einer Monopolstellung (im Vergleich zu
vollständiger Konkurrenz) ergibt.
15
Im Monopol reduziert sich die Konsumentenrente von dem Dreieck
𝑎𝐺𝑝𝑊 im Wettbewerbsmarkt auf das kleinere Dreieck 𝑎𝑀𝑝𝑀 . Der
Verlust an Konsumentenrente aus der Monopolstellung beträgt also
∆𝐾𝑅 = −𝐴 − 𝐵. Die Fläche B geht verloren, da nun Nachfrager mit
geringerer Zahlungsbereitschaft das Gut im Monopol nicht mehr
erwerben können. Diejenigen Konsumenten, deren marginale
Zahlungsbereitschaft hinreichend hoch ist müssen nun den höheren
Monopolpreis zahlen und verlieren daher Wohlfahrt in Höhe der
Fläche 𝐴. Entsprechend gewinnt der Monopolist Produzentenrente in
Höhe der Fläche A hinzu: Er kann nun für jede Outputeinheit bis zur
Monopolmenge 𝑄 𝑀 den höheren Monopolpreis verlangen. Um dies
tun zu können, muss er jedoch die Ausbringungsmenge reduzieren. Da
die Monopolmenge unterhalb der Wettbewerbsmenge liegt, geht dem
Produzenten – im Vergleich zur Produzentenrente im Wettbewerbsfall
– Produzentenrente in Höhe der Fläche C verloren. Insgesamt gilt
also: ∆𝑃𝑅 = +𝐴 − 𝐶 > 0, denn die Fläche A ist ganz offensichtlich
größer als die Fläche C. Wie zu erwarten gewinnt also der Produzent
aus der Monopolstellung.
16
Insgesamt entsteht ein Verlust an gesellschaftlicher Wohlfahrt aus der
Monopolstellung der gemessen werden kann als die Summe aus
Änderung der Produzentenrente und Änderung der Konsumentenrente. Es ist: ∆𝑆𝑊 = ∆𝐾𝑅 + ∆𝑃𝑅 = −𝐴 − 𝐵 + 𝐴 − 𝐶 = −𝐵 − 𝐶 < 0.
Die Ursache für den Verlust sozialer Wohlfahrt ist das im Monopolfall
kleinere Transaktionsvolumen im Marktgleichgewicht. Im Monopol
werden Tauschakte nicht realisiert, die unter Wohlfahrtsgesichtspunkten eigentlich stattfinden sollten.
Zeigen Sie, dass ein gewinnmaximierender Monopolist einen
Preisaufschlag über die Grenzkosten gemäß der Regel
d)
𝑃−𝐺𝐾
𝐺𝐾
1
= − 𝐸𝐷
𝑃
erhebt. Dabei bezeichnet 𝑃 den Preis, 𝐺𝐾 die Grenzkosten und
𝐸𝑃𝐷 die Preiselastizität der Nachfrage. Interpretieren Sie diese
Bedingung.
Die Gewinnfunktion des Monopolisten lautet:
𝜋 𝑀 = 𝑃(𝑄)𝑄 − 𝐶(𝑄)
Wir betrachten die notwendige Bedingung für ein Maximum des
Gewinns:
𝑑𝜋 𝑀
𝑑𝑄
=
𝑑𝑃(𝑄)
𝑑𝑄
𝑄 + 𝑃(𝑄) −
𝑑𝐶(𝑄)
𝑑𝑄
=0
Umformen liefert:
𝑃(𝑄) −
𝑑𝐶(𝑄)
𝑑𝑄
=−
𝑑𝑃(𝑄)
𝑑𝑄
𝑄
Durch Division mit 𝑃(𝑄) erhalten wir:
𝑃(𝑄)−
𝑑𝐶(𝑄)
𝑑𝑄
𝑃(𝑄)
Da
𝑑𝐶(𝑄)
𝑑𝑄
=−
𝑑𝑃(𝑄) 𝑄
𝑑𝑄
≡ 𝑀𝐶 und
𝑃(𝑄)
𝑑𝑃(𝑄) 𝑄
𝑑𝑄
1
≡ 𝐸𝐷 ergibt sich schließlich:
𝑃(𝑄)
𝑃
17
𝑃(𝑄)−𝑀𝐶(𝑄)
𝑃(𝑄)
1
= − 𝐸𝐷
𝑃
Der Preisaufschlag des Monopolisten über seine Grenzkosten verhält
sich also umgekehrt proportional zur Preiselastizität der Nachfrage.
Bei unelastischer Nachfrage ist der Preisaufschlag hoch, bei relativ
elastischer Nachfrage geringer. Das ist intuitiv plausibel: Ist die
Nachfrage elastisch, weichen die Nachfrager der Preiserhöhung des
Monopolisten aus (z.B. weil Substitute existieren). Bei unelastischer
Nachfrage können die Nachfrager der Preisforderung des Monopolisten nicht oder kaum ausweichen.
Aufgabe 3.2: Duopol
Die inverse Gesamtnachfrage in einem Markt für ein homogenes Gut
sei gegeben durch die Funktion
𝑃(𝑄) = 16 − 𝑄.
Dabei bezeichnet 𝑄 die Gesamtausbringungsmenge. Im Markt
befinden sich zwei Firmen, die zu identischen Kosten produzieren. Die
Kostenfunktionen seien der Einfachheit halber als linear angenommen:
𝐶𝑖 (𝑞𝑖 ) = 𝑐𝑞𝑖 , 𝑖 = 1,2,
wobei gelten soll, dass 𝑐 = 1.
a)
Nehmen sie an, dass beide Unternehmen versuchen, ihren
Gewinn durch die geeignete Wahl der Ausbringungsmenge zu
maximieren. Berechnen Sie das Gleichgewicht in diesem duopolistischen Markt (ermitteln Sie die gleichgewichtigen Ausbringungsmengen der beiden Anbieter sowie den gleichgewichtigen Marktpreis). Gehen Sie davon aus, dass die
Unternehmen ihre Entscheidungen simultan treffen. Erläutern
Sie, was man unter einer Reaktionsfunktion versteht und zeichnen Sie die Reaktionsfunktionen für die beiden Firmen.
Erläutern Sie, warum das Gleichgewicht durch den Schnittpunkt
der beiden Reaktionsfunktionen charakterisiert wird.
18
Die Gewinnfunktion der Firma 1 lautet:
𝜋1 = (16 − (𝑞1 + 𝑞2 ))𝑞1 − 𝑞1
(1)
Partielles Differenzieren von (1) bzgl. 𝑞1 liefert:
𝜕𝜋1
𝜕𝑞1
= 16 − 2𝑞1 − 𝑞2 − 1
(2)
Die notwendige Bedingung für ein Gewinnmaximum lautet:
15 − 2𝑞1 − 𝑞2 = 0 ⟺
15
1
𝑞1 = 2 − 2 𝑞2
(3)
(4)
Analog ermittelt man für Firma 2:
𝜋2 = (16 − (𝑞1 + 𝑞2 ))𝑞2 − 𝑞2
𝜕𝜋2
𝜕𝑞2
= 16 − 2𝑞2 − 𝑞1 − 1
15 − 2𝑞2 − 𝑞1 = 0 ⟺
15
1
𝑞2 = 2 − 2 𝑞1
(5)
(6)
(7)
(8)
Einsetzen von (8) in (4) liefert:
𝑞1 =
3
𝑞
4 1
15
2
=
1 15
1
− 2 ( 2 − 2 𝑞1 ) ⟺
30
4
−
15
4
(9)
⟺
𝑞1∗ = 5
(10)
Einsetzen von (10) in (8):
𝑞2∗ =
15
2
1
− 25 = 5
(11)
Damit ergibt sich der Preis als:
19
𝑃(𝑄 ∗ ) = 16 − 10 = 6
(12)
Die Reaktionsfunktionen sind durch (4) und (8) gegeben. Sie geben
die optimale Ausbringungsmenge für jede denkbare Ausbringungsmenge der jeweils anderen Firma an. Grafisch ergibt sich im
vorliegenden Beispiel:
𝑞2
15
10
𝑞1 (𝑞2 )
15
2
5
𝑞2 (𝑞1 )
0
5
15
2
10
15
𝑞1
Ein Gleichgewicht liegt in ökonomischen Zusammenhängen
regelmäßig dann vor, wenn keiner der beteiligten Akteure einen
Anreiz hat, von seinen gewählten Entscheidungen abzuweichen. Im
vorliegenden Duopolmarkt ist dies dann der Fall, wenn beide Firmen
ihren Gewinn maximieren. Die Gewinnmaxima für Firma 1 (2) liegen
auf der Reaktionsfunktion der Firma 1 (2). Ein simultanes Gewinnmaximum beider Firmen muss somit auf beiden Reaktionsfunktionen
liegen. Der einzige Punkt, der diese Forderung erfüllt, ist natürlich der
Schnittpunkt beider Reaktionsfunktionen.
b)
Erläutern Sie die Besonderheit der Entscheidungssituation im
Duopol. Was sind die wesentlichen Unterschiede zu der Entscheidungssituation, der sich ein Unternehmen bei voll-
20
kommener Konkurrenz einerseits, im Monopol andererseits gegenüber sieht?
Die Entscheidungen beider Firmen im Duopol sind wechselseitig
voneinander abhängig. Die optimale Ausbringungsentscheidung für
Firma 1 (2) hängt davon ab, wie sich Firma 2 (1) entscheidet. Man
spricht von strategischer Interaktion beider Firmen. Im Gegensatz
dazu findet zwischen Firmen in Märkten vollkommener Konkurrenz
keinerlei strategische Interaktion statt. Vielmehr passen sich die
Unternehmen alle an denselben, exogen gegebenen Marktpreis an, den
sie aufgrund ihrer nicht signifikanten Marktanteile nicht beeinflussen
können. Unternehmen in vollkommener Konkurrenz verhalten sich als
sogenannte Preisnehmer. Unternehmen in duopolistischen Märkten
hingegen üben durch ihre Ausbringungsentscheidung einen Einfluss
auf den sich bildenden Marktpreis aus – genau dadurch entsteht die
strategische Interdependenz. Im Monopol gibt es ohnehin keinerlei
Interaktion, da der Markt definitionsgemäß nur durch einen Anbieter
bedient wird.
c)
Berechnen Sie die gewinnmaximale Preis-Mengen-Kombination
eines monopolistischen Anbieters, der sich der oben angegebenen Marktnachfrage gegenüber sieht. Welcher Preis würde sich
bei vollkommener Konkurrenz einstellen? Vergleichen Sie Ihre
Lösungen für den Monopolfall und den Fall vollkommener Konkurrenz mit dem oben berechneten Gleichgewicht im Duopol.
Die Gewinnfunktion des Monopolisten lautet:
𝜋 𝑀 = (16 − 𝑄)𝑄 − 𝑄
(13)
Partielles Differenzieren bzgl. 𝑄 liefert:
21
𝜕𝜋 𝑀
𝜕𝑄
= 16 − 2𝑄 − 1
(14)
Die notwendige Bedingung für ein Gewinnmaximum ist:
15 − 2𝑄 = 0 ⟺
𝑄𝑀 =
(15)
15
(16)
2
Der Monopolpreis ergibt sich als:
𝑃(𝑄 𝑀 ) = 16 −
15
2
=
17
2
= 8,5
(17)
Im vollkommenen Wettbewerb würden die Anbieter zu
Grenzkostenpreisen von 𝑃𝑊 = 1 anbieten. Der Vergleich der
Marktformen ergibt:
8,5 = 𝑃𝑀 > 6 = 𝑃𝐷𝑈𝑂 > 1 = 𝑃𝑊
d)
Der französische Ökonom Bertrand hat bereits Ende des 19.
Jahrhunderts argumentiert, das Cournot-Modell sei unzutreffend, da Unternehmen nicht in Mengen, sondern über die Preise
konkurrieren. Welche Lösung ergibt sich im Duopol, wenn der
Wettbewerb der Firmen über den Preis ausgetragen wird? Halten Sie diese Lösung für plausibel?
Konkurrieren die Firmen über Preise, so kann es sein, dass sich bereits
zwei Firmen durch einen preislichen Unterbietungswettbewerb auf das
Niveau der Grenzkosten herunter konkurrieren. Der Anreiz zur
preislichen Unterbietung der anderen Firma ergibt sich aus der
Tatsache, dass der günstigere Anbieter (im Fall homogener Produkte)
die gesamte Marktnachfrage an sich bindet. Allerdings ist die Drohung
der preislichen Unterbietung nur glaubwürdig, wenn auch im Zweifel
die gesamte Marktnachfrage durch einen Anbieter allein befriedigt
werden kann. Dies erforderte jedoch, entsprechend große
Produktionskapazitäten vorzuhalten. Bezieht man die Kapazitätswahl
in das Entscheidungsproblem der duopolistischen Anbieter ein, so ist
es rational im Rahmen eines zweistufigen Spiels, zunächst auf Stufe 1
des Spiels eine Produktionskapazität in Höhe der Cournotmengen zu
22
wählen. Auf Stufe 2 ergibt sich dann derselbe Marktpreis, der sich
auch bei Cournot-Mengenwettbewerb im Duopolfall ergibt.
Aufgabe 3.3
Die Firma X kommt mit einem neuen Produkt auf den Markt. Sie sieht
sich mit einer fallenden inversen Unternehmensnachfragefunktion
𝑃(𝑞) = 12 − 𝑞 und einer konvexen Gesamtkostenfunktion 𝐾(𝑞) =
9 + 2𝑞 2 gegenüber.
a)
Berechnen Sie die kurzfristig optimale Ausbringungsmenge,
wenn Firma X über ein temporäres Monopol verfügt.
Die Gewinnfunktion des temporären Monopolisten lautet:
𝜋𝑋 = (12 − 𝑞)𝑞 − (9 + 2𝑞 2 )
(1)
Partielles Differenzieren nach q und Nullsetzen liefert:
𝜕𝜋𝑋
𝜕𝑞
= 12 − 2𝑞 − 4𝑞 = 0 ⟺
𝑞𝑋∗ = 2
b)
(2)
(3)
Berechnen Sie die Ausbringungsmenge der Firma X, die sich
langfristig bei monopolistischer Konkurrenz ergibt.
Langfristig wird Firma X durch Markteintritte von Substitutanbietern
gezwungen sein, im Tangentialpunkt der inversen Marktnachfragefunktion mit ihrer Durchschnittskostenfunktion anzubieten. Formal
muss daher gelten:
𝑃(𝑞) = 𝐷𝐾(𝑞) ⟺
12 − 𝑞 =
9+2𝑞 2
𝑞
(4)
⟺
12𝑞 − 𝑞 2 = 9 + 2𝑞 2 ⟺
23
𝑞 2 − 4𝑞 + 3 = 0
(5)
Die quadratische Gleichung (5) hat zwei Lösungen:
𝑞1,2 = 2 ± √4 − 3 = {3,1}
Relevant ist hier nur die zweite Lösung 𝑞2 = 1, da sich der
Tangentialpunkt im fallenden Bereich der DK-Funktion befinden muss
(das Minimum der DK-Funktion befindet sich bei 𝑞𝑚𝑖𝑛 = 3⁄√2).
24
Kapitel 4
Aufgabe 4.1: Bundesliga
Bis vor einiger Zeit galt in der Fußball-Bundesliga die Zwei-PunkteRegel: Der Sieger eines Spiels erhielt zwei Punkte, der Verlierer Null.
Bei Unentschieden gab es einen Punkt für jede Mannschaft. Ansonsten
galten natürlich die üblichen Annahmen: Offensive Mannschaften
gewinnen gegen defensive, bei gleichen Strategien endet ein Spiel
unentschieden.
Die Zwei-Punkte-Regel wurde durch die Drei-Punkte-Regel ersetzt,
weil die Drei-Punkte-Regel angeblich dazu führt, dass häufiger
offensiv gespielt wird. Zeigen Sie, dass bei der Formulierung dieser
Begründung der Chef-Spieltheoretiker des DFB seinen freien Tag
hatte: Analysieren Sie das Spiel sowohl für die Zwei-Punkte- als auch
für die Drei-Punkte-Regel.
Angaben in Punkten
Mannschaft 1
Mannschaft 2
offensiv
offensiv
defensiv
1, 1
2, 0
defensiv
0, 2
1, 1
Punkte für Mannschaft 1 = 1. Zahl. Punkte für Mannschaft 2 = 2. Zahl.
Angaben in Punkten
Mannschaft 1
Mannschaft 2
offensiv
offensiv
defensiv
1, 1
3, 0
defensiv
0, 3
1, 1
Punkte für Mannschaft 1 = 1. Zahl. Punkte für Mannschaft 2 = 2. Zahl.
Ein offensives Spiel zu spielen ist hier die dominante Strategie, da sie
mehr Punkte verspricht als eine defensive Spielstrategie. Außerdem ist
offensiv zu spielen immer die „beste Antwort“, egal welche Strategie
die andere Mannschaft wählt. Hierbei spielt es keine Rolle, ob man für
einen Sieg zwei oder drei Punkte erhält; es zählt nur, dass es mehr
Punkte verspricht, offensiv zu spielen als defensiv.
25
Aufgabe 4.2: Nash-Gleichgewichte
Betrachten Sie die folgende Auszahlungsmatrix:
Angaben in Geldeinheiten
Spieler 1
A
Spieler 2
A
B
𝑎, 𝑎
0, 0
B
0, 0
Auszahlung für 1 = 1. Zahl. Auszahlung für 2 = 2. Zahl.
a)
1, 1
Für welche Werte von 𝑎 ist {A, A} ein Nash-Gleichgewicht in
dominanten Strategien?
Für alle Werte größer 1, d.h. 𝑎 > 1, denn dann verspricht die
Strategiekombination {A, A} für beide Spieler die größte Auszahlung.
b)
Für welche Werte von 𝑎 ist {B, B} ein Nash-Gleichgewicht in
dominanten Strategien?
Für alle Werte kleiner 1, d.h. 𝑎 < 1, denn dann ist die Auszahlung für
beide Spieler bei der Kombination {B, B} größer als bei {A, A}.
c)
Beschreiben Sie die Nash-Gleichwichte des Spiels als Funktion
des Parameters 𝑎.
Grundsätzlich gilt folgende Beste-Antwort-Funktion zur Erreichung
von Nash-Gleichgewichten: 𝑠𝑖∗ = 𝑓𝑖 (𝑠𝑖𝑒) , d.h., dass die Funktion 𝑓𝑖
jedem Verhalten der anderen Spieler (𝑠𝑖𝑒 ) eine auszahlungsmaximierende Antwort 𝑠𝑖∗ zuordnet.
Hier ordnet die Funktion 𝑓(𝑎) jedem a, das größer ist als 1, das NashGleichgewicht {A, A} und jedem a, das kleiner ist als 1, das NashGleichgewicht {B, B} zu.
𝑓(𝑎) = {𝐴, 𝐴 |𝑎 > 1}
𝑓(𝑎) = {𝐵, 𝐵 |𝑎 < 1}
26
Aufgabe 4.3: Externe Kosten
Angenommen, Tassen aus Styropor werden mit konstanten
Grenzkosten von 4€ produziert. Die Marktnachfrage für dieses
Produkt sei 𝑄 𝐷 (𝑃) = 22 – 𝑃.
a)
Welche Produktionsmenge wird die Industrie wählen? Wie hoch
ist die Summe der Konsumenten- und Produzentenrente bei dieser Menge?
𝑄 𝐷 = 22 − 𝑃 ⟹ 𝑄 𝐷 = 22 − 4 ⟹ 𝑄 𝐷 = 18 𝑇𝑎𝑠𝑠𝑒𝑛
𝑃𝑅 = 0 (weil Grenzkosten = Marktpreis)
𝐾𝑅 = ½ ⋅ (22 − 4) ⋅ 18 = 162
b)
Diese Branche produziert nicht nur Styroportassen, sondern
verursacht auch Luftbelastungen. Die Kosten dieser Verschmutzung werden durch die Funktion der externen Grenzkosten
𝐸𝐺𝐾 = 0,2𝑄 beschrieben. Wie viele Styroportassen sollten vom
Effizienzstandpunkt aus (d.h. vom Standpunkt der Gesellschaft
aus) produziert werden?
𝐺𝐾𝑠𝑜𝑧 = 𝐺𝐾𝑝𝑟𝑖𝑣 + 𝐺𝐾𝑒𝑥𝑡 ⟹ 𝐺𝐾𝑠𝑜𝑧 = 4 + 0,2𝑄
Schnittpunkt 𝐺𝐾𝑠𝑜𝑧 mit der inversen Nachfragefunktion 𝑄 𝐷
22 − 𝑄 = 4 + 0,2𝑄 ⟹ 𝑄 𝑜𝑝𝑡 = 15 𝑢𝑛𝑑 𝑃𝑜𝑝𝑡 = 7, wobei 𝑄 𝑜𝑝𝑡 den
effizienten, d.h. sozial optimalen Output und 𝑃𝑜𝑝𝑡 den sozial
optimalen Marktpreis darstellen.
27
c)
Illustrieren Sie Ihre Antworten zu a) und b).
𝑃
𝑄𝐷
𝐺𝐾𝑠𝑜𝑧
9
8
𝑃𝑜𝑝𝑡
7
6
𝑃∗
5
𝐺𝐾𝑒𝑥𝑡
4
𝐺𝐾𝑝𝑟𝑖𝑣
3
2
1
0
2
4
6
8
10
12
14
16
18
20
𝑄𝑂𝑝𝑡 𝑄𝑊
d)
22
24
26
𝑄
Berechnen Sie die Steuer 𝑡 ∗ , welche den negativen externen
Effekt in b) optimal internalisiert. Wie hoch ist das Steuervolumen? Wie hoch ist der Netto-Wohlfahrtsgewinn durch diese
Steuer?
Eine Steuer 𝑡 muss der Differenz aus 𝐺𝐾𝑠𝑜𝑧 und 𝐺𝐾𝑝𝑟𝑖𝑣 im Optimum
entsprechen, um den negativen externen Effekt optimal zu
internalisieren.
𝑡 ∗ = 7 − 4 = 3 ⟹ Steuervolumen: 3 ⋅ 15 = 45
Der Netto-Wohlfahrtsgewinn durch die Steuer ergibt sich aus der
Differenz der Wohlfahrt vor der Steuer und der Wohlfahrt nach der
Steuer.
Wohlfahrt ohne Steuer: 𝐾𝑅 = 162 und 𝑃𝑅 = 0
1
Schaden aus dem externen Effekt = 2 ⋅ 18 ⋅ 3,667 = 33
⟹ 𝑊𝑜ℎ𝑙𝑓𝑎ℎ𝑟𝑡 = 162 + 0 − 33 = 129
Wohlfahrt mit Steuer:
1
𝐾𝑅 = 2 ⋅ (22 − 7) ⋅ 15 = 112,5 und 𝑃𝑅 = 0
28
1
Schaden aus dem externen Effekt = 2 ⋅ 15 ⋅ 3 = 22,5
Steuervolumen = 45
⟹ 𝑊𝑜ℎ𝑙𝑓𝑎ℎ𝑟𝑡 = 112,5 + 0 + 45 − 22,5 = 135
⟹ 𝑁𝑒𝑡𝑡𝑜 − 𝑊𝑜ℎ𝑙𝑓𝑎ℎ𝑟𝑡𝑠𝑔𝑒𝑤𝑖𝑛𝑛 𝑑𝑢𝑟𝑐ℎ 𝑆𝑡𝑒𝑢𝑒𝑟 = 135 − 129 = 6
Aufgabe 4.4: öffentliches Gut
Unterstellen Sie folgende Entscheidungssituation: Jeder Akteur
𝑖, 𝑖 = 1, … , 10, kann zu einem öffentlichen Gut beitragen. Die
Gewinnfunktion von i sei 𝜋𝑖 = −𝑞𝑖2 + 10𝑄, mit 𝑞𝑖 als Beitrag von i
zum öffentlichen Gut und 𝑄 = ∑10
𝑖=1 𝑞𝑖 als Summe der Beiträge aller
Akteure. Der individuelle Beitrag zum öffentlichen Gut verursacht
also quadratische Kosten für den Beitragenden und stiftet einen
Nutzen in Höhe von 10 für alle Akteure.
a)
Berechnen Sie den individuellen Beitrag 𝑞𝑖∗ und den Gesamtbeitrag 𝑄 ∗ aller Akteure im Nash-Gleichgewicht (∗) bei individuell
rationalem Verhalten. Berechnen Sie den individuellen und den
kollektiven Gewinn in dieser Situation (𝜋𝑖∗ und 𝛱 ∗). Inwieweit
unterscheidet sich das Gleichgewicht in diesem Spiel vom
Gleichgewicht im öffentlichen-Gut-Spiel in Abschnitt 4.3?
Ein Nash-Gleichgewicht (NE) ist dadurch definiert, dass jeder Akteur
seinen Gewinn maximiert gegeben das Verhalten aller anderen Spieler.
Zur Berechnung des Gewinnmaximums muss die Gewinnfunktion 𝜋𝑖
über 𝑞𝑖 maximiert werden. Der Gruppenbeitrag 𝑄 wird dabei
gedanklich zerlegt in den eigenen Beitrag 𝑞𝑖 und in den Beitrag aller
anderen Akteure 𝑄𝑗 = ∑𝑗≠𝑖 𝑞𝑗 bzw. 𝑄 = 𝑞𝑖 + 𝑄𝑗 = 𝑞𝑖 + ∑𝑗≠𝑖 𝑞𝑗 .
𝜋𝑖 = −𝑞𝑖2 + 10𝑄 = −𝑞𝑖2 + 10(𝑞𝑖 + ∑𝑗≠𝑖 𝑞𝑗 ) → 𝑚𝑎𝑥!
Dafür leitet man die Gewinnfunktion nach 𝑞𝑖 ab und setzt diese
Ableitung dann gleich Null:
𝜕𝜋𝑖
𝜕𝑞𝑖
= −2𝑞𝑖 + 10 = 0 ⟺ −2𝑞𝑖𝑁𝐸 + 10 = 0 ⇔ 𝑞𝑖𝑁𝐸 = 5
Die beste Antwort von Akteur 𝑖 ist unabhängig vom Verhalte der
anderen Akteure. Es liegt also eine dominante Strategie und damit
auch ein Nash-Gleichgewicht in dominanten Strategien.
Der Gesamtbeitrag im Nash-Gleichgewicht beträgt somit:
29
𝑁𝐸
𝑄 𝑁𝐸 = ∑10
= 50.
𝑖=1 𝑞𝑖
Der individuelle Gewinn im Nash-Gleichgewicht ist:
𝜋𝑖𝑁𝐸 = −𝑞𝑖2 + 10𝑄 = 475
Der kollektive Gewinn: 𝛱 𝑁𝐸 = 10 ⋅ 475 = 4.750
Dieses Spiel unterscheidet sich insofern von dem Beispiel in Abschnitt
4.3, als dass hier im Nash-Gleichgewicht in dominanten Strategien ein
positiver Beitrag von jedem Spieler geleistet wird.
b)
Berechnen Sie den individuellen Beitrag 𝑞𝑖𝑆𝑂 und den Gesamtbeitrag 𝑄 𝑆𝑂 aller Akteure im sozialen Optimum (𝑆𝑂) bei kollektiv
rationalem Verhalten sowie die zugehörigen Gewinne 𝜋𝑖𝑆𝑂 und
𝛱 𝑆𝑂 .
Zunächst muss Π(𝑄) ermittelt werden. Hierfür werden die Gewinne
2
aller Akteure aufsummiert mit Π(𝑄) = ∑10
𝑖=1( − 𝑞𝑖 + 10𝑄).
1
Da wir es mit identischen Spielern zu tun haben, gilt 10 𝑄 = 𝑞𝑖 ⟺
𝑄 = 10𝑞𝑖 . Wir können somit Π(𝑄) auch schreiben:
2
2
Π(𝑄) = ∑10
𝑖=1( − 𝑞𝑖 + 10𝑄) = 10(−𝑞𝑖 + 10𝑄)
1
1
= − 10 (10𝑞𝑖 )(10𝑞𝑖 ) + 100𝑄 = − 10 𝑄 2 + 100𝑄
Das kollektive Gewinnmaximum ist:
𝜕Π
2
= − 10 𝑄 + 100 = 0 ⇔ 𝑄 ∗ = 500 und 𝑞 ∗ = 𝑞𝑖∗ = 50.
𝜕𝑄
Der individuelle Gewinn im sozialen Optimum ist:
𝜋𝑖∗ = −𝑞𝑖2 + 10𝑄 = −(502 ) + 10 ∙ 500 = 2.500
Der kollektive Gewinn im sozialen Optimum ist:
𝛱 ∗ = 10 ⋅ 2500 = 25.000
Allgemein: Bei der Bereitstellung des öffentlichen Gutes gibt es einen
Unterschied zwischen individueller Rationalität, der Nutzenmaximierung des einzelnen Akteurs, und kollektiver Rationalität, der
Nutzenmaximierung der Gruppe. Der Nutzen im Nash-Gleichgewicht
ist geringer als in einer Situation, in der sich alle Akteure kollektiv
rational verhalten würden. Die Akteure befinden sich offensichtlich in
einem „sozialen Dilemma“: Individuell rationales Verhalten führt zu
einem ineffizienten, kollektiv irrationalen Ergebnis.
30
c)
Stellen Sie das Problem graphisch dar.
Die Abb. zeigt das Problem graphisch. Die individuellen Grenzkosten
des Beitrags sind 𝐺𝐾𝑖 = 2𝑞𝑖 . Der individuelle Grenznutzen ist
𝐺𝑁𝑖 = 10 und der soziale Grenznutzen ist 𝐺𝑁 = 100.
𝐺𝑁
𝐺𝐾𝑖 = 2𝑞𝑖
100
𝐺𝑁
90
80
70
60
50
40
30
20
𝐺𝑁𝑖
10
5
d)
10
15
20
25
30
35
40
45
50
𝑞𝑖
Interpretieren Sie die Werte aus a) und b). Zeigen Sie, dass die
Situation in b) kein Gleichgewicht ist (Hinweis: Zeigen Sie, dass
sich einseitiges Abweichen von der kooperativen Lösung in b)
lohnt).
Angenommen 𝑖 = 1 wählt 𝑞1∗ = 5, alle anderen 𝑖 wählen 𝑞𝑖∗ = 50 als
Beitrag. Für diese Individualbeiträge ergäbe sich folgender
Gesamtbeitrag:
𝑄 ∗ = 9 ∙ 𝑞𝑖 + 𝑞1 = 9 ∙ 50 + 5 = 455
Die individuellen Gewinne wären:
𝜋1∗ = −𝑞12 + 10𝑄 ∗ = −(52 ) + 10 ∙ 455 = 4.525
𝜋𝑖∗ = −𝑞𝑖2 + 10𝑄 ∗ = −(502 ) + 10 ∙ 455 = 2.050
Der kollektive Gewinn wäre:
𝛱 ∗ = 9 ⋅ 2050 + 1 ∙ 4525 = 22.975
31
Daraus wird deutlich, dass sich ein einseitiges Abweichen von der
Kooperativen Lösung für den Abweichenden lohnt und somit in b)
kein Gleichgewicht vorliegt.
Aufgabe 4.5: Market for Lemons
Angenommen, es gibt einen Gebrauchtwagenmarkt mit drei VW Golf.
Jeder Golf wird von je einem Händler angeboten, der die Qualität des
Wagens kennt. Die Preise der Wagen sind 1500€, 3500€ und 5000€.
Die Qualität ist positiv mit dem Preis korreliert. Es gibt drei
potentielle Käufer, die je nach Qualität eine unterschiedliche
Zahlungsbereitschaft (ZB) haben: Die (ZB) für hohe (mittlere,
schlechte) Qualität ist 6.000€ (4.000€, 2.000€).
a)
Angenommen, die Qualität ist gleichverteilt und die Käufer
können die Qualität nicht beobachten. Welche Transaktionen
finden statt? Wie hoch ist der Wohlfahrtsgewinn?
Die Transaktion zwischen dem Anbieter des Wagens mit niedrigem
Preis und dem Käufer mit durchschnittlicher Zahlungsbereitschaft
(von 4.000€) findet statt: Verkauf zu 1.500€. Die Transaktion
zwischen dem Anbieter des Wagens mit mittlerem Preis und dem
Käufer mit durchschnittlicher Zahlungsbereitschaft findet statt:
Verkauf zu 3.500€.
Die Transaktion zwischen dem Anbieter des Wagens mit hohem Preis
und dem Käufer mit durchschnittliche Zahlungsbereitschaft findet
nicht statt, da der Preis von 5.000€ über der Zahlungsbereitschaft von
4.000€ liegt.
⟹ 𝑊𝑜ℎ𝑙𝑓𝑎ℎ𝑟𝑡𝑔𝑒𝑤𝑖𝑛𝑛 = 1.500€ + 3.500€ = 5.000€
b)
Gehen Sie nun von vollständiger Information aus. Welche
Transaktionen finden statt? Wie hoch ist der Wohlfahrtsgewinn?
Die Transaktion zwischen dem Anbieter des Wagens mit niedrigem
Preis und dem Käufer mit niedriger Zahlungsbereitschaft findet statt:
Verkauf zu 1.500€. Die Transaktion zwischen dem Anbieter des
Wagens mit mittlerem Preis und dem Käufer mit mittlerer Zahlungsbereitschaft findet statt: Verkauf zu 3.500€. Die Transaktion zwischen
dem Anbieter des Wagens mit hohem Preis und dem Käufer mit hoher
Zahlungsbereitschaft findet statt: Verkauf zu 5.000€.
⟹ 𝑊𝑜ℎ𝑙𝑓𝑎ℎ𝑟𝑡𝑔𝑒𝑤𝑖𝑛𝑛 = 1.500€ + 3.500€ + 5.000€ = 10.000€
32
c)
Diskutieren Sie Lösungsmöglichkeiten für das Marktversagen.
Das Problem bei dieser Art des Marktversagens liegt in der
systematisch ungleich verteilten, also asymmetrischen Information.
Lösungsmöglichkeiten beruhen also in erster Linie auf einem
Ausgleich des Informationsrückstandes, hier auf Seiten der
Nachfrager.
Im vorliegenden Fall der asymmetrischen Information beim
Gebrauchtwagenkauf könnten die Gebrauchtwagenverkäufer Signale
setzen, welche eine gute Qualität ihrer Wagen glaubhaft machen. Dies
könnte beispielsweise über Garantieleistungen erfolgen. Garantien
sind ein glaubhaftes Versprechen guter Qualität, da man im Falle
schlechter Qualität den Wagen wieder zurückbringen kann. Somit
werden nur diejenigen Verkäufer eine Garantie anbieten, die auch
wirklich Wagen mit guter Qualität verkaufen, denn andernfalls würden
die eingeforderten Garantieleistungen zu hohe Kosten verursachen.
Eine weitere, aber langwierigere Möglichkeit besteht darin, sich als
Anbieter von Wägen mit hoher Qualität einen guten Ruf
(„Reputation“) aufzubauen und diesen durch das fortlaufende
Anbieten von Qualitätswägen aufrechtzuerhalten. Dadurch wird es
möglich, höhere Preise zu verlangen, was die höheren Kosten von
guten Autos ausgleicht und den Verkauf lukrativ macht.
33
Kapitel 5
Aufgabe 5.1: Konsumententheorie I
Gegeben sei folgende Nutzenfunktion: 𝑈 = 𝑈(𝑥, 𝑦) = 𝑥 𝛼 𝑦1−𝛼 , wobei
𝑥 und 𝑦 die Konsummengen zweier beliebiger Güter bezeichnen. Der
Preis für eine Einheit 𝑥 betrage 𝑃𝑥 = 2, der Preis für eine Einheit 𝑦
𝑃𝑦 = 1. Das Einkommen des Konsumenten betrage 7 Geldeinheiten.
Es sei bekannt, dass 𝛼 = 0,25.
a)
Zeigen Sie, dass die Steigung der zu U gehörigen Indifferenz𝑑𝑦
𝛼 𝑦
kurven allgemein gegeben ist als 𝑑𝑥 = 1−𝛼 𝑥 .
Wir bilden das totale Differential der Nutzenfunktion:
𝑑𝑈 =
𝜕𝑈
𝜕𝑥
𝜕𝑈
𝑑𝑥 + 𝜕𝑦 𝑑𝑦
Die Nutzenänderung entlang einer Indifferenzkurve ist Null. Zu
fordern ist daher:
𝑑𝑈 = 0 ⟺
𝜕𝑈
𝜕𝑥
𝜕𝑈
𝑑𝑥 + 𝜕𝑦 𝑑𝑦 = 0 ⟺
𝑑𝑥
𝑑𝑦
=−
𝜕𝑈
𝜕𝑦
𝜕𝑈
𝜕𝑥
Die Steigung der Indifferenzkurve ist also gegeben durch den
Quotienten der Grenznutzen der beiden Güter.
Für die Nutzenfunktion 𝑈(𝑥, 𝑦) = 𝑥 𝛼 𝑦 1−𝛼 ergibt sich:
𝑑𝑥
𝑑𝑦
b)
=−
(1−𝛼)𝑥 𝛼 𝑦 −𝛼
𝛼𝑥 𝛼−1 𝑦 1−𝛼
=−
1−𝛼
𝛼
𝑥 𝛼−(𝛼−1) 𝑦 −𝛼−(1−𝛼) = −
1−𝛼 𝑥
𝛼 𝑦
Berechnen Sie numerisch das optimale Güterbündel!
Die Beantwortung von (b) erfolgt im Rahmen von (c) und (d).
c)
Zeigen Sie allgemein, dass die optimale Nachfragemenge für 𝑥
sich immer invers zum Güterpreis verhält und gegeben ist als
𝐼
𝑥 𝑜𝑝𝑡 = 𝑃 (2−𝛼).
𝑥
34
Zeigen Sie, dass sich auch die optimale Güternachfrage nach 𝑦
invers zum Preis des Gutes verhält und allgemein gegeben ist
𝐼(1−𝛼)
als 𝑦 𝑜𝑝𝑡 = 𝑃 𝛼(2−𝛼).
d)
𝑦
Das optimale Güterbündel ist durch den Tangentialpunkt von
Indifferenzkurve und Budgetgerade charakterisiert. Die Steigungen
beider Funktionen stimmen exakt überein. Es muss also gelten:
−
1−𝛼 𝑥
𝛼 𝑦
=−
𝑝𝑦
⟺𝑥=𝑦
𝑝𝑥
𝛼𝑝𝑦
𝑝𝑥 (1−𝛼)
Aus der Budgetrestriktion ermittelt man:
𝐼
𝑝𝑦
𝑥=𝑝 −𝑝 𝑦
𝑥
𝑥
Gleichsetzen:
𝑦𝑝
𝛼𝑝𝑦
𝑥 (1−𝛼)
𝑝𝑦
𝐼
1
= 𝑝 − 𝑝 𝑦 ⟺ 𝑦𝛼𝑝𝑦 (1−𝛼 + 1) = 𝐼 ⟺
𝑥
𝑥
1−𝛼
𝐼
𝑦 𝑜𝑝𝑡 = 𝛼(2−𝛼) 𝑝
𝑦
Dann folgt sofort:
𝑥 𝑜𝑝𝑡 = 𝑦 𝑜𝑝𝑡 𝑝
𝛼𝑝𝑦
1−𝛼
𝑥 (1−𝛼)
𝐼
⟺ 𝑥 𝑜𝑝𝑡 = 𝛼(2−𝛼) 𝑝
𝛼𝑝𝑦
𝑦 𝑝𝑥 (1−𝛼)
⟺
𝐼
𝑥 𝑜𝑝𝑡 = (2−𝛼)𝑝
𝑥
Numerisch ergibt sich:
7
𝑥 𝑜𝑝𝑡 = (2−0,25)2 = 2
1−0,25
7
𝑦 𝑜𝑝𝑡 = 0,25(2−0,25) 1 = 12
e)
Welche Nachfragemengen ergeben sich bei einer Verdopplung
des Einkommens des Konsumenten auf 14 Geldeinheiten?
35
Da die optimalen Güternachfragen proportional zum Einkommen sind,
verdoppeln sich mit dem Einkommen auch die optimalen
Nachfragemengen:
14
𝑥 𝑜𝑝𝑡 = (2−0,25)2 = 4
1−0,25
𝑦 𝑜𝑝𝑡 = 0,25(2−0,25)
f)
14
1
= 24
Welcher Effekt auf die optimalen Konsummengen ergibt sich,
wenn sich der Güterpreis für 𝑥 (𝑦) halbiert (verdoppelt)?
Da die optimalen Güternachfragen invers zum Eigenpreis sind, führt
eine Verdoppelung (Halbierung) des Preises zur einer Halbierung
(Verdoppelung) der optimalen Nachfragemengen:
7
𝑥 𝑜𝑝𝑡 (𝑝𝑥 = 4) = (2−0,25)4 = 1
7
𝑥 𝑜𝑝𝑡 (𝑝𝑥 = 1) = (2−0,25)1 = 4
𝑦 𝑜𝑝𝑡 (𝑝𝑦 = 2) =
1−0,25
7
0,25(2−0,25) 2
1−0,25
=6
7
𝑦 𝑜𝑝𝑡 (𝑝𝑦 = 0,5) = 0,25(2−0,25) 0,5 = 6
Aufgabe 5.2: Konsumententheorie II
Gegeben sei die folgende Schar von Indifferenzkurven für zwei Güter
𝑐
𝑥 und 𝑦: 𝑦 = 𝑎𝑥 , 𝑐 > 0, 𝑎 > 0. Die Budgetmenge des Konsumenten ist
gegeben als 𝐼 = 𝑃𝑦 𝑦 + 𝑃𝑥 𝑥. Dabei bezeichnen 𝑦 und 𝑥 die konsumierten Mengen, 𝑃𝑦 , 𝑃𝑥 die Güterpreise pro Mengeneinheit.
a)
Durch welche Bedingung ist das optimale Güterbündel
charakterisiert?
Das optimale Güterbündel ist charakterisiert durch den Tangentialpunkt von Indifferenzkurve und Budgetgerade. Im Tangentialpunkt
stimmen die Steigung der Indifferenzkurve, die Grenzrate der
36
Substitution, und die Steigung der Budgetgerade (das Preisverhältnis
beider Güter) überein. Formal muss gelten:
𝑑𝑦
𝑑𝑥
𝑃
𝑐 1
𝑃
= − 𝑃𝑥 ⇔ − 𝑎 𝑥 2 = − 𝑃𝑥
𝑦
𝑦
Zeigen Sie, dass das optimale Güterbündel allgemein gegeben
b)
𝑐 𝑃𝑦
𝑐
ist als 𝑥 𝑜𝑝𝑡 = √𝑎 𝑃
, 𝑦 𝑜𝑝𝑡 = 𝑎𝑥 𝑜𝑝𝑡.
𝑥
Aus der Tangentialbedingung ergibt sich:
𝑐 1
𝑃
𝑐 𝑃𝑦
𝑐 𝑃𝑦
𝑥
𝑥
− 𝑎 𝑥 2 = − 𝑃𝑥 ⇔ 𝑥 2 = 𝑎 𝑃 ⇔ 𝑥 𝑜𝑝𝑡 = √𝑎 𝑃
𝑦
da lediglich die positive Wurzel als ökonomisch sinnvolle Lösung
infrage kommt. Damit ist:
𝑐
𝑦 𝑜𝑝𝑡 = 𝑎𝑥 𝑜𝑝𝑡 =
c)
𝑐
𝑐 𝑃𝑦
𝑎 𝑃𝑥
𝑎√
Welche optimalen Mengen ergeben sich für 𝑎 = 𝑐 = 1,
𝑃𝑦 = 8 und 𝑃𝑥 = 2?
Für 𝑎 = 𝑐 = 1, 𝑃𝑌 = 8 und 𝑃𝑥 = 2 ergibt sich:
8
𝑥 𝑜𝑝𝑡 = √2 = 2
1
𝑦 𝑜𝑝𝑡 = 2
Aufgabe 5.3: Produktionstheorie I
Gegeben sei die folgende Produktionsfunktion
𝑄 = 𝑄(𝐾, 𝐿) = 𝐾 𝛼 𝐿1−𝛼 , 0 < 𝛼 < 1.
Zeigen Sie, dass die Funktion positive aber abnehmende Grenzprodukte der Arbeit und des Kapitals aufweist.
Wir bilden die ersten partiellen Ableitungen der Produktionsfunktion:
37
𝜕𝑄
= 𝛼𝐾 𝛼−1 𝐿1−𝛼 > 0 ⟺ 𝛼 > 0
𝜕𝐾
𝜕𝑄
𝜕𝐿
= 𝛼(1 − 𝛼)𝐾 𝛼−1 𝐿−𝛼 > 0 ⟺ 𝛼 > 0 ∧ 𝛼 < 1
Um abnehmende Grenzprodukte zu zeigen, betrachten wir die zweiten
partiellen Ableitungen:
𝜕2 𝑄
𝜕𝐾2
𝜕2 𝑄
𝜕𝐿2
= 𝛼(𝛼 − 1)𝐾 𝛼−2 𝐿1−𝛼 < 0 ⟺ 𝛼 < 1
= −𝛼 2 (1 − 𝛼)𝐾 𝛼−1 𝐿−𝛼−1 < 0 ⟺ 𝛼 < 1
Aufgabe 5.4: Minimalkostenkombination
𝑐
Gegeben sei die folgende Isoquantenschar: 𝐾 = 𝑎𝐿, wobei 𝐾 und 𝐿
die Faktoreinsatzmengen an Kapital und Arbeit bezeichnen. Die
Isokostengerade sei gegeben als 𝐶 = 𝑤𝐿 + 𝑟𝐾, mit 𝑤 als Lohnsatz
und 𝑟 als Kapitalkostensatz (Zinssatz).
a)
Ermitteln Sie allgemein die Minimalkostenkombination!
Die MKK ist durch den Tangentialpunkt von Isoquante und Isokostengerade charakterisiert. Im Tangentialpunkt stimmen die Steigungen
beider Funktionen exakt überein. Die Steigung der Isoquante ermittelt
man leicht als:
𝜕𝐾
𝜕𝐿
𝑐
= − 𝑎𝐿2
𝑤
Die Steigung der Isokostengerade ist − 𝑟 . Also muss gelten:
𝑤
𝑐
𝑐 𝑟
− 𝑟 = − 𝑎𝐿2 ⟺ 𝐿𝑜𝑝𝑡 = √𝑎 𝑤
Daraus folgt sofort:
𝑐
𝐾 𝑜𝑝𝑡 = 𝑎𝐿𝑜𝑝𝑡 =
𝑐
𝑐𝑟
𝑎√
𝑎𝑤
𝑐2
𝑐𝑤
⟺ 𝐾 𝑜𝑝𝑡 = √ 2 𝑐 𝑟 = √𝑎 𝑟
𝑎
𝑎𝑤
38
b)
Wie wird die optimale Arbeitsnachfrage auf Änderungen des
Lohnsatzes reagieren? Begründen Sie Ihr Ergebnis mathematisch und ökonomisch!
Um zu zeigen, wie die Arbeitsnachfrage eines kostenminimierenden
Unternehmens auf Lohnsatzänderungen reagiert, differenzieren wir
(mit Hilfe der Kettenregel!) die optimale Arbeitsnachfrage nach w:
𝜕𝐿 𝑜𝑝𝑡
𝜕𝑤
1 1
=2
𝑐𝑟
√
𝑎𝑤
−𝑎𝑐𝑟
(𝑎2 𝑤2 ) < 0
Verteuert sich also ceteris paribus der Faktor Arbeit, so nimmt die
Nachfrage nach dem Faktor ab.
Aufgabe 5.5: Kostentheorie
Gegeben sei die Produktionsfunktion
𝑄 = 𝑄(𝐾, 𝐿) = 𝐾 𝛼 𝐿1−𝛼 , 0 < 𝛼 < 1.
Der Lohnsatz pro Einheit Arbeit sei 𝑤 = 15, die Fixkosten der
Produktion liegen bei 𝐹𝐾 = 10.000. Vervollständigen Sie die
folgende Tabelle, d.h., berechnen Sie für die angegebenen Ausbringungsmengen i) das Grenzprodukt des Faktors Arbeit (GPA); ii) die
Grenzkosten der Produktion (GK); iii) die Gesamtkosten der
Produktion (K) sowie die iv) Durchschnittskosten (DK).
K
100
100
100
100
100
L
100
150
200
250
300
𝛼
0,75
0,75
0,75
0,75
0,75
Q
100,000
110,668
118,921
125,743
131,607
GPA
--0,213
0,165
0,136
0,103
w
15
15
15
15
15
GK
--70,203
90,881
109,928
127,898
FK
10.000
10.000
10.000
10.000
10.000
K
11.500
12.250
13.000
13.750
14.500
DK
110,691
109,317
109.350
110,176
Zunächst können mit Hilfe der Produktionsfunktion die Outputmengen für die unterschiedlichen Faktoreinsatzkombinationen berechnet
werden. Für 𝐾 = 100, 𝐿 = 150 ergibt sich beispielsweise:
𝑄 = 1000,75 1500,25 ≅ 110,668
Analog ermittelt man leicht die übrigen Mengen.
39
Aus den Outputänderungen lassen sich dann die Grenzprodukte der
Arbeit bestimmen. Man erhält:
𝐺𝑃𝐴1 ≡
∆𝑄1
𝐺𝑃𝐴2 ≡
∆𝑄2
𝐺𝑃𝐴3 ≡
∆𝑄3
𝐺𝑃𝐴4 ≡
∆𝑄4
∆𝐿1
∆𝐿2
∆𝐿3
∆𝐿4
=
10,668
=
8,253
=
6,823
=
5,171
50
50
50
50
≅ 0,213
≅ 0,165
≅ 0,136
≅ 0,103
Da gilt:
∆𝐶
𝐺𝐾 ≡ ∆𝑄 =
∆𝑉𝐶
∆𝑄
=
𝑤∆𝐿
∆𝑄
𝑤
= 𝐺𝑃𝐴
lassen sich auch die zugehörigen Grenzkosten leicht berechnen:
𝐺𝐾1 ≡
𝑤∆𝐿1
𝐺𝐾2 ≡
𝑤∆𝐿2
𝐺𝐾3 ≡
𝑤∆𝐿3
𝐺𝐾4 ≡
𝑤∆𝐿4
∆𝑄1
∆𝑄2
∆𝑄3
∆𝑄4
15∗50
= 10,668 ≅ 70,203
=
15∗50
=
15∗50
=
15∗50
8,253
6,823
5,171
≅ 90,881
≅ 109,928
≅ 127,898
Wegen
∆𝐶
𝐺𝐾 ≡ ∆𝑄 =
∆𝑉𝐶
∆𝑄
kann die Änderung der variablen Kosten leicht berechnet werden als:
𝐺𝐾∆𝑄 = ∆𝑉𝐶
40
Man berechnet:
∆𝑉𝐶1 = 70,203 ∗ 10,668 = 750
∆𝑉𝐶2 = 90,881 ∗ 8,253 = 750
∆𝑉𝐶3 = 109,928 ∗ 6,823 = 750
∆𝑉𝐶4 = 127,898 ∗ 5,171 = 750
Die gesamten variablen Kosten bei der ursprünglichen Produktionsmenge von 𝑄 = 100 belaufen sich natürlich auf 𝑉𝐶 = 𝑤 ∗ 𝐿 = 15 ∗
100 = 1500. Damit ergeben sich die variablen Kosten für die
unterschiedlichen Produktionsniveaus als
𝑉𝐶1 = 1.500 + 750 = 2.250
𝑉𝐶2 = 2.250 + 750 = 3.000
𝑉𝐶3 = 3.000 + 750 = 3.750
𝑉𝐶4 = 3.750 + 750 = 4.500
Gegeben das Fixkostenniveau von 10.000 ergeben sich die gesamten
Produktionskosten als:
𝐶1 = 12.250, 𝐶2 = 13.000, 𝐶3 = 13.750, 𝐶4 = 14.500
Damit lassen sich die Stückkosten ermitteln als:
𝐴𝐶1 =
𝐶1
12.250
=
= 110,691
𝑄1 110,668
𝐴𝐶2 =
𝐶2
13.000
=
= 109,317
𝑄2 118,921
𝐴𝐶3 =
𝐶3
13.750
=
= 109,350
𝑄3 125,743
41
𝐴𝐶4 =
𝐶4
14.500
=
= 110,176
𝑄4 131,607
Die Stückkosten fallen also zunächst, steigen dann aber wieder an.
Aufgabe 5.6: Produktionstheorie II
a)
Zeigen Sie allgemein, dass sich Isoquanten nicht schneiden
können.
Angenommen, zwei Isoquanten würden sich schneiden, wie in der
folgenden Abbildung dargestellt:
2
1
Isoquante 1 repräsentiert das höhere Outputniveau 𝑄1 > 𝑄2 .
Weisen die beiden Isoquanten einen Schnittpunkt auf, so wäre es
möglich, den höheren Output 𝑄1 im Punkt A mit geringeren
Einsatzmengen beider Produktionsfaktoren zu produzieren – was
offensichtlich nicht sein kann.
b)
Gegeben sei die Produktionsfunktion
𝑄 = 𝑄(𝐾, 𝐿) = 𝐾 𝛼 𝐿1−𝛼 , 0 < 𝛼 < 1.
Zeigen Sie, dass die zugehörigen Isoquanten die Steigung
𝑑𝐾
1−𝛼 𝐾
= − 𝛼 𝐿 aufweisen. Wie verlaufen die Isoquanten?
𝑑𝐿
42
Wir betrachten das totale Differential der Produktionsfunktion und
setzen Null:
𝜕𝑄
𝜕𝑄
𝑑𝑄 = 𝜕𝐾 𝑑𝑘 + 𝜕𝐿 𝑑𝐿 = 0 ⇔
𝛼𝐾 𝛼−1 𝐿1−𝛼 𝑑𝐾 + (1 − 𝛼)𝐾 𝛼 𝐿−𝛼 𝑑𝐿 = 0 ⇔
𝑑𝐾
𝑑𝐿
=−
1−𝛼 𝐾𝛼
𝛼
𝐾 𝛼−1
𝐿−𝛼
𝐿1−𝛼
=−
1−𝛼 𝐾
𝛼
𝐿
Die Isoquanten sind durch eine Schar paralleler Hyperbeln gegeben.
43