Wärmelehre

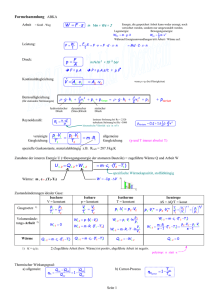
Wärmelehre
1
1. TEMPERATUR UND TEILCHENBEWEGUNG
1
Temperatur und Teilchenbewegung
Jeder Körper besteht aus unendlich vielen Teilchen, den Atomen und Molekülen. Der Körper
kann sich in drei Zustandsformen (auch Aggregatzustände genannt) befinden: fest, flüssig und
gasförmig.
1.1
1.1.1
Aggregatzustände
Feste Körper
Die Teilchen (Atome / Moleküle) eines festen Körpers befindet sich in einer geordneten Gitterstruktur, können sich also nicht gegeneinander umher bewegen. Dennnoch befinden sie sich
nicht im Ruhezustand. In der Tat vibrieren die Teilchen eines Körpers auf ihrer Stelle hin- und
her.
Abbildung 1: Teilchen eines Körpers in festem Zustand
1.1.2
Flüssigkeiten
In einer Flüssigkeit bewegen sich die Teilchen relativ zueinander umher. Trotzdem bleiben alle
Moleküle und Atome noch dicht zusammen. Es gibt keine geordnete Struktur mehr.
Abbildung 2: Teilchen eines Körpers in flüssigem Zustand
2
c Y. Reiser
1. TEMPERATUR UND TEILCHENBEWEGUNG
1.1.3
Gase
In Gasen ist die Bewegung der Teilchen völlig ungeordnet. Die Atome / Moleküle bewegen sich
sehr schnell umher. Alle Teilchen sind völlig unabhängig voneinander und die Distanz zwischen
ihnen ist äußerst groß.
Abbildung 3: Teilchen eines Körpers im gasförmigen Zustand
1.2
Temperatur und innere Energie
Definition:
Die Temperatur eines Körpers ist ein Maß für die Bewegungsgeschwindigkeit seiner Teilchen.
Bei einem festen Körper ist die Temperatur umso höher, je schneller/heftiger die Teilchen auf
der Stelle vibrieren. Bei Flüssigkeiten und Gasen bewegen sich die Teilchen schneller umher,
wenn sich die Temperatur erhöht.
Da die Teilchen in allen Zustandsformen in Bewegung sind (entweder sie vibrieren oder sie
bewegen sich umher), besitzen sie immer auch kinetische Energie.
Definition:
Die innere Energie eines Körpers ist die Summer der kinetischen Energien all seiner Teilchen.
Man kann die Temperatur also auch sagen, dass:
Die Temperatur eines Körpers ein Maß für die mittlere kinetische Energie der Körperteilchen
ist.
3
c Y. Reiser
1. TEMPERATUR UND TEILCHENBEWEGUNG
1.3
Messen von Temperaturen
Temperaturen werden mit einem Thermometer gemessen.
Es gibt zwei Kategorien von Thermometern:
1.3.1
Kontakt-Thermometer
− Widerstandsthermometer : ein elektrischer Widerstand verändert seinen Wert mit der
Temperatur (für die meisten Leiter gilt: je höher die Temperatur, desto größer der elektrische Widerstand). Der Widerstand kann elektronisch gemessen und umgewandelt als
Temperatur in einem Display angezeigt werden. Messbereich: −273 ◦ C bis 3000 ◦ C.
− Dilatationsthermometer : Diese Thermometer können entweder eine Flüssigkeit oder ein
Gas enthalten. Das enthaltene Medium dehnt sich bei steigender Temperatur aus. Flüssigkeitsthermometer sind meist mit gefärbtem Alkohol oder auch Quecksilber gefüllt.
Messbereich: −250 ◦ C bis 1000 ◦ C.
Skala
Glasröhrchen
Flüssigkeit
Vorratsgefäß
Abbildung 4: Flüssigkeitsthermometer
Steigt die Temperatur, dehnt sich die Flüssigkeit aus. Der Pegel im Glasröhrchen steigt.
− Bimetall-Thermometer : Bei dieser Art von Thermometer wird die Temperatur von einem
Bimetallstreifen gemessen, der sich im Messfühler befindet. Der Bimetallstreifen besteht
aus zwei Metallstreifen, die an den Bandenden miteinander verbunden sind. dabei besteht
jeder Streifen aus einem anderen Metall. Da jedes Metall sich unterschiedlich stark mit
steigender Temperatur ausdehnt, verbiegt sich der Bimetallstreifen umso mehr, je stärker
er erwärmt wird.
− ...
4
c Y. Reiser
1. TEMPERATUR UND TEILCHENBEWEGUNG
1.3.2
Kontaktlose Thermometer
− das Pyrometer : Für glühende Objekte gibt es ein visuelles Verfahren, bei dem das Glühlicht einer Wolframbandlampe (Glühlampe mit Wolfram-Band statt einer -Wendel) mit
dem zu messenden Objekt zur Deckung gebracht wird. Man kann nun den Strom der
Lampe so lange verändern, bis ihr Bild vor dem Messobjekt verschwindet - dann ist die
Bandtemperatur gleich der des Messobjektes. Der Einstellknopf des Lampenstromes hat
zum Ablesen der Temperatur eine Temperaturskala. Eine solche Messapparatur wird als
Glühfadenpyrometer bezeichnet und gehört zur Gruppe der Vergleichspyrometer. Messbereich : 500 ◦ C bis 3000 ◦ C
− das Temperatur-Spektrometer : wird hauptsächlich zur Bestimmung der Temperaturen von
Sternen eingesetzt. Die Sterne haben unterschiedliche Farben. Die Ursache dieser Farben
liegt in den unterschiedlichen Oberflächentemperaturen. So hat z.B. ein bläuclicher Stern
eine höhere Temperatur als ein rötlicher Stern. Messbereich : 1000 ◦ C bis 20000 ◦ C
− das Infrarot-Thermometer : alle Körper, die wärmer als 0 K (null Kelvin = absoluter
Nullpunkt) sind, senden elektromagnetische Strahlung aus (ab 400 ◦ C beginnt der Körper
dann im sichtbaren Bereich (dunkelrot) zu strahlen). Bis zu einer gewissen Temperatur
hat diese Strahlung ihr Maximum im Infrarotbereich. Misst man die Wellenlänge dieses
Strahlungsmaximums kann man die Temperatur eines Körpers ziemlich genau auf Distanz
bestimmen.
1.4
1.4.1
Temperatureinheiten
Grad Celsius
Das Grad Celsius (◦ C) ist eine Temperatureinheit, die 1744 eingeführt worden ist. Erfunden
wurde diese Einheit vom schwedischen Astronom und Physiker Anders Celsius(1701-1744).
Diese Einheit der Temperatur wird weltweit benutzt, mit Ausnahme von einigen wenigen Ländern wie den amerikanischen Staaten.
Die Celsius-Skala hat zwei Fixpunkte:
− der Wert 0 ◦ C entspricht dem Schmelzpunkt/Erstarrungspunkt des Wassers bei normalem
Luftdruck (1013, 25 hPa).
− der Wert 100 ◦ C entspricht dem Siedepunkt/Kondensationspunkt des Wassers, ebenfall
bei Normaldruck.
Die Celsius-Skala wird zwischen diesen beiden Fixpunkten in 100 gleich lange Segmente eingeteilt.
Das Formelzeichen, welches zur Angabe einer Temperatur in Grad Celsius verwendet wird ist
der griechische Buchstabe „Theta”: θ.
Beispiel: θ = 23, 5 ◦ C
5
c Y. Reiser
1. TEMPERATUR UND TEILCHENBEWEGUNG
1.4.2
Grad Fahrenheit
Das Grad Fahrenheit (◦ F) ist eine andere Maßeinheit der Temperatur, die auf den deutschen
Physiker Daniel Gabriel Fahrenheit(1686-1736) zurückgeht und im Jahr 1724 eingeführt wurde. Heute wird diese Einheit ausschließlich in den amerikanischen Staaten, in Bélize und den
Caïman-Inseln verwendet.
Fahrenheit wählte folgende Fixpunkte als Referenz für seine Temperaturskala:
− der Wert 0 ◦ F entspricht der tiefsten Temperatur, die Fahrenheit im besonders kalten
Winter 1708/1709 in seiner Geburtsstadt Danzig messen konnte.
− der Wert 100 ◦ F entspricht der Bluttemperatur eines Pferdes.
Das Formelzeichen, mit dem eine Temperatur in Grad Fahrenheit angegeben wird ist tF .
Beispiel: tF = 95, 3◦ F.
Umwandlung:
tF (◦ F) = 1, 8 · θ(◦ C) + 32
θ(◦ C) =
tF (◦ F) − 32
1, 8
Beispiele :
θ = 22, 0 ◦ C : tF = (1, 8 · 22 + 32) ◦ F = 71, 6 ◦ F
◦
tF = 85, 0 ◦ F : θ = 85,0−32
C = 29, 4 ◦ C.
1,8
1.4.3
Kelvin
Die SI-Einheit der Temperatur ist Kelvin
Beachte : Die Einheit ist „Kelvin”, nicht „Grad Kelvin” !
Die Einheit ist nach William Thomson1 benannt, besser bekannt unter seinem späteren Namen Lord Kelvin.
Diese Temperatureinheit hängt direkt mit der inneren Energie eines Körpers (s. S. 3) zusammen:
wenn ein Körper gar keine interne Energie mehr hat (dies ist dann der Fall wenn seine Teilchen
nicht mehr vibrieren), dann hat er eine Temperatur von 0 K (i.e. der Körper hat den „absoluten
Nullpunkt” erreicht). Dies ist die tiefste Temperatur, auf die ein Körper abgekühlt werden kann.
Das Formelzeichen für Temperaturen, die in Kevin angegeben sind, ist T .
Beispiel: T = 285 K.
1
William Thomson, 1824-1907
6
c Y. Reiser
1. TEMPERATUR UND TEILCHENBEWEGUNG
Umwandlung:
T (K) = θ(◦ C) + 273
θ(◦ C) = T (K) − 273
Beispiele:
θ = 32 ◦ C : T = (32 + 273) K = 306 K
T = 295 K : θ = (295 − 273) ◦ C = 22 ◦ C
1.5
Temperaturdifferenzen
Wenn eine Temperatur von einem Wert θ1 auf einen Wert θ2 ändert, so ist die Temperaturdifferenz in ◦ C gleich :
∆θ = θ2 − θ1
In Kelvin umgewandelt ist T1 = θ1 + 273 und T2 = θ2 + 273.
Die Temperaturdifferenz in K ist also:
∆T
⇔ ∆T
⇔ ∆T
⇔ ∆T
⇔ ∆T
= T2 − T1
= (θ2 + 273) − (θ1 + 273)
✟− θ −✟
✟
= θ2 + ✟
273
273
1
= θ2 − θ1
= ∆θ
Eine Temperaturdifferenz, in ◦ C angegeben, hat also genau den gleichen Wert wie in K !
∆T = ∆θ
Achtung! Dies gilt nicht für Temperaturunterschiede in ◦ F : ∆tF 6=∆θ.
7
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
2
Temperaturausdehnung von Körpern
2.1
Längenausdehnung von festen Körpern
2.1.1
Versuch
22,8
◦
C
Thermometer
Wasserkreislauf
Pumpe
Heizwendel
Messuhr
Rohr
∆l
1/100 mm
Das Wasser im Behälter wird mit einer elektrischen Heizspirale auf verschiedene Temperaturen
gebracht. Die Pumpe befördert das erwärmte Wasser durch einen Kreislauf, der ein austauschbares Rohr enthält. Die Temperatur θ des Rohrs entspricht so nach kurzer Zeit der jeweiligen
Temperatur des durchfließenden Wassers und kann somit einfach mit einem Thermometer im
Wasserbad gemessen werden.
Die Ausgangslänge l0 des Rohrs ist seine Länge bei der Ausgangstemperatur θ0 .
Das Rohr ist an einer Seite fest eingespannt, an der anderen Seite drückt es gegen den Mechanismus einer Messuhr, die eine Längenänderung ∆l des Rohrs mit großer Präzision (1/100 mm)
messen kann.
Wir messen für jedes Rohr die Längenänderung ∆l = l − l0 für verschiedene Temperaturänderungen ∆T = ∆θ = θ − θ0
8
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Material: __________ ; Ausgangslänge : l0 =__________ m
θ(◦ C)
∆T (K)
∆l(mm)
∆l(m)
Material: __________ ; Ausgangslänge : l0 =__________ m
θ(◦ C)
∆T (K)
∆l(mm)
∆l(m)
Material: __________ ; Ausgangslänge : l0 =__________ m
θ(◦ C)
∆T (K)
∆l(mm)
9
∆l(m)
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Wir stellen für jedes Rohr die Längenänderung ∆l zur Temperaturänderung ∆T grafisch dar.
Wir fügen jeder Messreihe ihre Näherungsgerade hinzu.
Wir stellen fest:
Die Messpunkte liegen (von Messfehlern abgesehen) auf einer Nullpunktgeraden. Die Steigung
dieser Geraden hängt vom Material ab, aus dem das Rohr besteht.
Schlussfolgerung:
Für ein bestimmtes Rohr gilt:
∆l ∼ ∆T
(1)
Experimentell könnte man zusätzlich überprüfen, daß die Längenänderung ∆l auch proportional zur Anfangslänge l0 ist. Dies leuchtet ein, denn wenn man zum Beispiel 2 (oder 3 oder
n) identische Rohre mit jeweils der gleichen Anfangslänge l0 hätte, dann würde man auch erwarten, daß jedes einzelne Rohr sich bei einer Temperaturänderung von ∆T um die Länge ∆l
ausdehnt, die Gesamtausdehnung aller Rohre wäre somit 2 · ∆l (bzw. 3 · ∆l oder n · ∆l). Also
gilt zusätzlich:
∆l ∼ l0
(2)
Kombiniert man (1) und (2), so kann man sagen, daß:
∆l ∼ l0 · ∆T
Die Proportionalität kann man als Gleichung anschreiben, wenn man eine Proportionalitätskonstante hinzufügt. Auf diese Weise erhält man das „Längenausdehnungsgesetz”:
∆l = α · l0 · ∆T
Die Proportionalitätskonstante α ist dabei der „spezifische Längenausdehnungskoeffizient” (auch „llinearer Ausdehnungskoeffizient) genannt). Er ist ein Merkmal vom Material, aus
dem ein Körper besteht und wird in der Einheit 1/K angegeben.
Auswertung der Messungen aus dem Versuch:
Da wir in der Grafik die Längenausdehnung auf die y-Achse aufgetragen haben, die Temperaturänderung ∆T auf die x-Achse, können wir die Gleichung y = Steigung · x der Nullpunktgeraden
aus unserer Graphik zu jedem Rohr anschreiben als:
∆l = Steigung · ∆T
(∗)
Die theoretische Formel lautet:
∆l = α · l0 · ∆T
(∗∗)
Vergleicht man (*) und (**), so sieht man:
Steigung = α · l0
10
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Da wir die Anfangslänge l0 der Rohre kennen, können wir somit den spez. Längenausdehnungskoeffizienten für jedes Rohr berechnen:
α=
2.1.2
Steigung
l0
Ursache der Längenausdehnung
In einem festen Körper sind die Teilchen (Atome / Moleküle) eines Körpers dicht zusammen in
ihrer Gitterstruktur angeordnet. Wird die Temperatur erhöht, so vibrieren alle Teilchen heftiger
auf ihrer Stelle. Dadurch nimmt jedes einzelne Teilchen mehr Platz ein. Bei einer großen Länge
summiert sich dieser Platzbedarf der einzelnen Teilchen auf die makroskopische Länge ∆l : der
Körper dehnt sich messbar aus.
niedrigere Temperatur
höhere Temperatur : Ausdehnung
Abbildung 5: Fester Körper bei unterschiedlichen Temperaturen
11
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
2.1.3
Längenausdehnungskoeffizienten
Stoff
Blei
Magnesium
Aluminium
Silber
Kupfer
Gold
Nickel
Beton
Eisen
Stahl
Beryllium
Platin
Chrom
Wolfram
Diamant
α(1/K)
28,9 · 10−6
24,8 · 10−6
23,1 · 10−6
18,9 · 10−6
16,5 · 10−6
14,2 · 10−6
13,4 · 10−6
12,0 · 10−6
11,8 · 10−6
12,0 · 10−6
11,3 · 10−6
8,8 · 10−6
4,9 · 10−6
4,5 · 10−6
1,18 · 10−6
Tabelle 1: Längenausdehnungskoeffizienten einiger Stoffe (bei 20 ◦ C)
2.1.4
Rechenbeispiel
Ein Bleirohr hat bei 15, 8 ◦ C eine Länge von 12, 8 m. Wie groß ist die Länge bei einer Temperatur von 85, 6 ◦ C?
l0 = 12, 800 m ; αP b = 28 · 10−6 1/K ; ∆T = ∆θ = θ2 − θ1 = 69, 8 K
∆l = α · l0 · ∆T
⇔ ∆l = 12, 800 m · 28, 9 · 10−6
1
· 69, 8 K
K
⇔ ∆l = 0, 026 m (= 26 mm)
Länge bei 85, 6 ◦ C:
l = l0 + ∆l
⇔ l = 12, 800 m + 0, 026 m
⇔ l = 12, 826 m
2.1.5
Längenausdehnung im Alltag
Die Längenausdehnung kann bei entsprechend langen Körpern zu Problemen führen, wenn diese großen Temperaturschwankungen ausgesetzt werden:
Zugschienen können sich so stark verformen, dass sie unbrauchbar werden. Bei der Konstruktion
von Stahlbrücken müssen an mindestens einem Ende Lager verbaut werden, die die Längenänderung bei starken Temperaturschwankungen ermöglichen. In langen Gaspipelines und auch
12
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Heizungsrohren müssen Ausdehnungsschleifen eingebaut werden, um Risse bei einer Verformung durch Längenausdehnung zu vermeiden.
Beim Bau von Gebäuden aus Beton werden üblicherweise Stahlmatten verwendet, um die Zugfestigkeit der Bauteile zu verstärken (Beton alleine bröckelt bei zu hoher Zugbelastung). Dies
ist nur deshalb möglich, weil der Wert der Ausdehnungskoeffizienten von Stahl und Beton gleich
ist.
2.2
2.2.1
Volumenänderung von festen Körpern und Flüssigkeiten
Volumenänderung von festen Körpern
Ein fester Körper dehnt sich nicht nur in der Länge, sondern auch in seiner Breite und seiner
Höhe nach der Formel ∆l = α · l0 · ∆T aus. Daraus folgt, dass das Volumen sich bei einer Temperaturänderung erhöht.
Die Volumenänderung lässt sich mit einer Formel berechnen, die der der Längenausdehnung
fast gleich ist:
∆V = γ · V0 · ∆T
V0 ist das Ausgangsvolumen, γ (,griechischer Buchstabe „Gamma”) ist der „spezifische Volumenausdehnungskoeffizient. Er wird, genau wie der Längenausdehnungskoeffizient in der
Einheit 1/K angegeben.
Für feste Körper gilt:
γ ≈ 3 · α (∗)2
Ausgehend von den Längenausdehnungskoeffizienten können die entspr. Volumenausdehungskoeffizienten fester Stoffe also leicht berechnet werden.
ein Würfel der Kantenlänge l0 hat das Volumen V0 = l0 3 . Bei Erwärmung um ∆T hat jede Kante die Länge
l = l0 + α · l0 · ∆T = l0 (1 + α · ∆T ). Das Volumen beträgt nun V = [l0 (1 + α · ∆T )]3 = (l0 )3 (1 + α · ∆T )3 .
Weil α · ∆T eine sehr kleine Zahl ist, macht man nur einen sehr kleinen Fehler, wenn man (1 + α · ∆T )3 durch
(1 + 3 · α · ∆T ) ersetzt.
2
13
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Versuch zur Volumenausdehnung fester Körper:
Eine Kugel aus Metall passt bei Raumtemperatur noch gerade so durch einen Ring (s. Abb. 6).
Nun wird die Kugel mit einem Bunsenbrenner stark erwärmt.
Man beobachtet :
− die stark erwärmte Kugel passt nicht mehr durch den Ring
− nach Abkühlung fällt die Kugel wieder durch den Ring
Abbildung 6: Versuch : Volumenausdehnung einer Kugel
2.2.2
Volumenänderung von Flüssigkeiten
Die Formel (*) gilt auch für die Volumenänderung von Flüssigkeiten. Die Volumenausdehnungskoeffizienten für Flüssigkeiten kann man aus Tabellen entnehmen (bzw. natürlich auch
experimentell bestimmen), da es hier keine Längenasudehnungskoeffizienten gibt.
14
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
Stoff
γ(1/K)
Quecksilber 0,1811 · 10−3
Glycerin 0,520 · 10−3
Mineralöl
0,7 · 10−3
Essigsäure
1,08 · 10−3
Benzol
1,14 · 10−3
Ethanol
1,40 · 10−3
Aceton
1,46 · 10−3
Methanol
1,49 · 10−3
◦
Wasser(0 C) -0,068 · 10−3
Wasser(20 ◦ C) 0,207 · 10−3
Wasser(100 ◦ C) 0,782 · 10−3
Tabelle 2: Volumenausdehnungskoeffizienten einiger Flüssigkeiten (bei 20 ◦ C)
Der Volumenausdehnungskoeffizient von Flüssigkeiten hat einen höheren Wert als der von festen
Körpern. Daher ändern Flüssigkeiten ihr Volumen bei Erwärmung stärker als feste Körper.
2.2.3
Rechenbeispiel
Glycerin hat bei −5 ◦ C ein Volumen von 8, 500 l. Wie groß ist das Volumen bei 55 ◦ C?
V0 = 8, 5 l ; γ = 0, 520 · 10−3 1/K ; ∆T = ∆θ = θ2 − θ1 = 60 K
∆V = γ · V0 · ∆T
⇔ ∆V = 0, 520 · 10−3 1/K · 8, 500 l · 60 K
⇔ ∆V = 0, 265 l
Volumen bei 55 ◦ C :
V = V0 + ∆V
⇔ V = 8, 500 l + 0, 265 l
⇔ V = 8, 765 l
2.2.4
Anomalie des Wassers
In der Tabelle 2 kann man sehen, dass beim Wasser je nach Temperaturbereich unterschiedliche
Werte für den Ausdehnungskoeffizienten γ angegeben sind. Vor allem aber fällt auf, dass γ für
Wasser bei 0 ◦ C einen negativen Wert hat, was bedeutet, dass flüssiges Wasser oberhalb von
0 ◦ C bei Erwärmung zusammenzieht.
In der Tat kann man beobachten, dass das Volumen von Wasser zwischen 0 ◦ C und 4 ◦ C abnimmt. Oberhalb von 4 ◦ C nimmt das Volumen bei weiterer Erwärmung wieder zu:
15
c Y. Reiser
2. TEMPERATURAUSDEHNUNG VON KÖRPERN
0 ◦C
2 ◦C
4 ◦C
6 ◦C
8 ◦C
10 ◦ C
Abbildung 7: Wasservolumen bei steigender Temperatur
Dieses Phänomen wird „Anomalie des Wassers” genannt. Da eine bestimmte Menge Wasser
immer die gleiche Masse m hat, das Volumen V aber bei 4 ◦ C am kleinsten ist, ist eine Konse)!
quenz, dass die Dichte von Wasser bei 4 ◦ C am größten ist (Dichte : ρ = m
V
Die Anomalie des Wassers (auch „Dichteanomalie” genannt) ist wichtig für das Leben in Gewässern kälterer Klimazonen. Sommer wie Winter findet man in tiefen Gewässern das dichteste
Wasser, also das mit einer Temperatur von 4 ◦ C, in der untersten Schicht. Lebewesen können
sich hier also vor zu hohen bzw zu tiefen Temperaturen nahe der Wasseroberfläche schützen:
Sommer
Winter
8 ◦C
7
6
5
4
0 ◦C
1
2
3
4
Abbildung 8: Temperaturschichtung in einem See
16
c Y. Reiser
3. WÄRME
3
Wärme
3.1
Definition, Formelzeichen und Einheit
Im vorigen Kapitel (Mechanik) haben wir gelernt, dass sich die mechanische Energie eines Körpers erhöht, wenn man Arbeit auf den Körper verrichtet (so führt Hubarbeit zu pot. Lageenergie,
Beschleunigungsarbeit führt zu kinetischer Energie und Spannarbeit führt zu Spannenergie).
Wir haben gelernt, dass Arbeit eine Übertragungsmöglichkeit mechanischer Energie ist (s. S. ??).
Genau so wie die mechanische Energie einer Körpers verändert werden kann, kann auch seine
innere Energie (s. S. 3) größer oder kleiner werden:
− nimmt die innere Energie eines Körpers ab (d.h. er wird kälter), dann gibt er Wärme ab.
− nimmt die innere Energie eines Körpers zu (d.h. er wird wärmer), dann nimmt er Wärme
auf.
Daher folgt die Definition:
Wärme ist eine Übertragungsart von innerer Energie.
Das Formelzeichen der Wärme ist Q (cf. Formelzeichen der Arbeit : W ). Da Wärme eine Übertragung von Energie ist, ist auch ihre Einheit gleich der der Energie : Joule (J).
Achtung!
Die Wörter „Temperatur” und „Wärme” haben unterschiedliche Bedeutungen. Im Alltag werden beide Worte oft falsch verwendet (im physikalischen Sinne). Die Temperatur bezeichnet
einen energetischen Zustand, den ein Körper haben kann. Wärme ist Energie, die ein Körper
aufnehmen oder abgeben kann.
3.2
Übertragung und Umwandlung von innerer Energie
Wärmeübertragung findet zwischen zwei Körpern unterschiedlicher Temperatur statt. So kühlt
eine heiße Suppe im kalten Teller ab, während sich die kalte Milch aus dem Kühlschrank darin
erwärmt.
Wärme geht spontan immer vom wärmeren auf den kälteren Körper über.
Das Energieerhaltungsgesetz gilt (selbstverständlich) auch für die innere Energie:
Gibt ein Körper eine bestimmte Menge innerer Energie ab, so erhält ein anderer Körper
diese Menge Energie. Innere Energie kann weder verloren, noch erzeugt werden.
Innere Energie kann durch Wärmeleitung, durch Wärmeströmung oder durch Wärmestrahlung
übertragen werden.
17
c Y. Reiser
3. WÄRME
3.2.1
Wärmeleitung
Wärmeübertragung durch Wärmeleitung findet im Innern der Körper statt. Wärmeleitung
findet ohne Bewegung der Materie statt.
Wärmeleitung kann sowohl innerhalb eines einzelnen Körpers stattfinden als auch durch den
Kontakt zweier Körper.
Versuch:
Abbildung 9: Versuch - Wärmeleitung
Wir erwärmen einen Zylinder aus Metall, an den 3 Röhrchen angebracht sind (jeweils aus Kupfer, aus Messing und aus Eisen). In die offenen Enden werden Streichhölzer eingeführt.
Wir beobachten, dass das Streichholz im Kupferröhrchen sich schon kurz nach Beginn der
Erwärmung entzündet. Es folgt das Streichholz im Messingröhrchen. Das Streichholz im Eisenröhrchen entzündet sich zuletzt.
Erklärung:
Kollisionen der Teilchen (Atome oder Moleküle) mit ihren Nachbarteilchen führen dazu, dass
sich die heftigen Vibrationen an der Stelle der Erwärmung nach und nach im ganzen Metall
ausbreiten. Die Ausbreitungsgeschwindigkeit hängt dabei vom jeweiligen Metall ab.
18
c Y. Reiser
3. WÄRME
Abbildung 10: Kontakt zwischen einem warmen und einem kalten Körper
− gute Wärmeleiter: im Allgemeinen sind die Metalle, die elektrischen Strom gut leiten,
auch gute Wärmeleiter (so zum Beispiel Kupfer, den man deshalb oft zur Herstellung von
Töpfen verwendet).
− schlechte Wärmeleiter (Wärmeisolatoren): z.B. Holz (Griffe von Pfannen, ...), Kork (als
Telleruntersetzer), Luft (Doppelverglasung), ...
19
c Y. Reiser
3. WÄRME
3.2.2
Wärmeströmung
Wärmeströmung findet durch Bewegung von Materie in Flüssigkeiten und Gasen statt. Die
Teilchen übertragen so innere Energie, indem sie sich selbst von einem Ort an einen anderen
bewegen. Diese Bewegungen stellen einen sog. Konvektionsstrom dar.
Versuch:
Abbildung 11: Versuch - Wärmeströmung
Erklärung:
Das von der Flamme erwärmte Wasser dehnt sich aus. Seine Dichte nimmt ab, so dass es sich
nach oben bewegt. Nach und nach setzt sich das ganze Wasser in Bewegung : es entsteht eine
Konvektionsströmung. Das warme Wasser steigt auf einer Seite nach oben, das kältere sinkt
auf der anderen Seite nach unten. Die innere Energie der Teilchen wird so zusammen mit den
Teilchen selbst von einem an einen anderen Ort gebracht.
Anwendungen:
− Die Luft, die sich oberhalb eines Heizkörpers befindet, wird erwärmt. Sie steigt nach oben,
kühlt hier ab und steigt auf der anderen Seite des Raumes wieder nach unten. Die so entstehende Wärmeströmung ermöglicht somit die Erwärmung der Luft im ganzen Raum.
20
c Y. Reiser
3. WÄRME
− Wärmeströmung spielt auch eine große Rolle im Wettergeschehen. Heiße Erdoberflächen
lassen warme Luft aufsteigen, die anschließend wieder zu kälteren Oberflächen absteigt.
Oberhalb der heißen Flächen bilden sich durch die Konvektionsströme oft die sog. Cumuluswolken (das Wasser, das sich in den Konvektionsströmen befindet kondensiert bei den
kalten Temperaturen der oberen Luftschichten).
− ...
3.2.3
Wärmestrahlung
Alle Körper, die wärmer als 0 K (absoluter Nullpunkt) sind, strahlen elektromagnetische
Wellen aus. Die abgestrahlte Energie hängt von der Temperatur des Körpers ab.
Versuch:
Parabolspiegel
Glühlampe
Streichholz
Lichtstrahl
Abbildung 12: Versuch - Wärmestrahlung
Eine Glühlampe wird in den Brennpunkt eines Parabolspiegels gesetzt. Die Licht- und Wärmestrahlen, die die Lampe aussendet, werden vom Spiegel so reflektiert, dass sie anschliessend
parallel sind und sich so auf den zweiten Parabolspiegel zu bewegen. Im Brennpunkt dieses
zweiten Spiegels befindet sich ein Streichholz. Kurz nachdem die Lampe eingeschaltet wurde
entzündet sich das Streichholz.
Wärme wurde durch Strahlung von der Glühlampe zum Streichholz übertragen.
Anwendungen:
− die Energie der Sonne erreicht die Erde durch das Vakuum im Weltall ausschließlich über
Wärmestrahlung.
− schwarze/dunkle Oberflächen absorbieren Wärmestrahlung stärker und erwärmen sich
daher schneller als weiße/helle Flächen.
− ...
21
c Y. Reiser
3. WÄRME
3.3
Wärmeisolierung
Möchte man verhindern, dass ein System mit seiner Umgebung Wärme austauscht, muss man
das System thermisch isolieren. Man muss also sowohl Wärmeleitung als auch Wärmeströmung
und Wärmestrahlung verhindern. Dies geschieht, indem man das System von „adiabatischen
Wänden” umgibt. In der Praxis gibt es die perfekt adiabatische Wand nicht. Man kann die
Wärmeübertragung aber auf eine Minimum reduzieren.
Anwednungen:
− Thermoskannen sind Kannen/Flasschen, die aus doppelten Wänden bestehen. Die Luft,
die sich zwischen den beiden Wänden befindet, verhindert Wärmeleitung. Zudem sind die
Wände innen und außen mit spiegelnden Oberflächen überzogen. Wärmestrahlung wird
so ganz einfach reflektiert (und kann das innere einer waren Thermoskanne nicht verlassen
bzw von aussen nicht in eine kalte Thermoskanne eindringen).
− Doppelverglasung: die Luft (oder ein Edelgas) zwischen den zwei Fensterscheiben einer
Doopelverglasung verhindert Wärmeleitung zwischen dem Innenraum und der Außenwelt.
− ...
22
c Y. Reiser
4. KALORIMETRIE
4
Kalorimetrie
Die Kalorimetrie ist der Teil der Wärmelehre, die sich mit dem Messen von Wärmemengen
befasst. Dies sind zum Beispiel die Wärmemengen, die man braucht, um die Temperatur eines
Körpers zu erhöhen und seinen Aggregatzustand zu ändern oder auch die Menge an Wärme,
die ein Körper abgibt, wenn er sich abkühlt.
4.1
4.1.1
Einführungsversuch
Zusammenhang zw. Wärme und Temperaturunterschied
Mit einem Tauchsieder erwärmen wir 1 kg Wasser. Der Tauchsieder wandelt die elektrische
Energie, die er aus dem Stromnetz bezieht, vollständig in Wärme um und gibt diese Wärme
dann an das Wasser ab. Die elektrische Leistung P des Tauchsieders ist gleich der elektrischen
Energie Eél. , die er aufnimmt, geteilt durch das Zeitintervall ∆t dieser Energieabgabe:
Eél.
Q
=
∆t
∆t
Kennt man die elektrische Leistung Pel. des Tauchsieders, kann man also ganz einfach berechnen,
welche Wärmemenge das Wasser nach einer bestimmten Zeit erhalten hat:
Pél. =
Q = P · ∆t
Wir erwärmen Wasser der Masse m=______ mit einem Tauchsieder der el. Leistung
Pel =______ und messen dabei den Temperaturanstieg ∆T zu verschiedenen Zeitpunkten.
(∆T = θ − θ0 . Dabei ist θ0 die Anfangstemperatur des Wassers.)
22.8
◦
C
Abbildung 13: Erwärmen von Wasser
23
c Y. Reiser
4. KALORIMETRIE
∆t(s) Q(J) θ(◦C) ∆T (K)
Vergleichen wir den Temperaturanstieg ∆T mit der zugeführten Wärme Q, so stellen wir fest:
Die Temperaturerhöhung des Wasserd ist proportional zur Wärme, die es erhalten hat:
Q ∼ ∆T
4.1.2
Zusammenhang zw. Wärme und Masse
Wir wiederholen den vorherigen Versuch mit der doppelten Masse an Wasser.
m=______ ; P = _____
∆t(s) Q(J) θ(◦C) ∆T (K)
Wir stellen fest: Die Zeit, die für eine gleiche Temperaturerhöhung ∆T wie bei der einfachen
Masse benötigt wird, ist doppelt so lang.
Schlussfolgerung:
24
c Y. Reiser
4. KALORIMETRIE
Die vom Wasser aufgenommene Wärme ist proportional zu seiner Masse:
Q∼m
4.2
Spezifische Wärmekapazität
Die vorangegangenen Versuche zeigten, dass:
Q ∼ m
Q ∼ ∆T
Wir schlussfolgern daraus, dass:
⇔
Q
m · ∆T
Q ∼ m · ∆T
= c (Kontante)(∗)
Die Proportionalitätskonstante c wird spezifische Wärmekapazität genannt. Sie ist eine Eigentschaft des Stoffs, aus dem der Körper besteht, der die Wärme erhält/abgibt. c wird in kgJ· K
(Joule pro Kilogramm Kelvin) angegeben.
Die spezifische Wärmekapazität c entspricht der Wärmemenge, die von 1 kg eines Stoff
abgegeben/aufgenommen wird, wenn dessen Temperatur sich um 1 K (oder 1 ◦ C)
verändert.
Die Wärmemenge, die man einem Körper der Masse m und der spez. Wärmekapazität c zufügen
muss, damit sich seine Temperatur um den Betrag ∆T ändert, lässt sich also mit der Formel
berechnen, die man erhält, indem man die Formel (*) umstellt:
Q = m · c ∆T
c( kgJ· K )
Stoff
Quecksilber
Kupfer
Eisen
Beton
Aluminium
Luft
Natrium
Olivenöl
Petroleum
Wasser
Eis
Wasserstoff
139
389
456
800 à 1000
900
1000
1256
2000
2093
4186
2060
14300
Tabelle 3: Spezifische Wärmekapazitäten einiger Stoffe
25
c Y. Reiser
4. KALORIMETRIE
Es fällt auf, dass Wasser eine besonders hohe spezifische Wärmekapazität hat. Aus diesem
Grund verwendet man gerade Wasser, um die Wärme in Zentralheizungen schnell überall hin
zu übertragen oder auch um große Mengen an Abwärme, die in einem Verbrennungsmotor entsteht, zum Kühler zu transportieren.
Bemerkung: die Kalorie - eine alte Einheit der Wärme/Energie:
Um 1 g Wasser um 1 ◦ C zu erwärmen, muss es folgende Wärmemenge erhalten:
Q = m · c · ∆T = 0, 001 kg · 4186 J/kgK · 1 K = 4, 186 J.
Diese Wärmemenge entspricht der veralteten Energieeinheit „Kalorie” (cal).
Eine Kalorie ist die Energie, die man 1 g Wasser zufügen muss, damit sich seine
Temperatur um 1 ◦ C erhöht:
1 cal = 4, 186 J
Oft verwendet wird auch noch die „Kilocalorie”:
1 kcal=1000 cal=4186 J=4,186 kJ
4.3
Positive / Negative Wärme
Es wurde festgelegt:
− Erhält ein Körper Wärme, so hat die von ihm ausgetauschte Wärme ein positives Vorzeichen: Q>0.
− Gibt ein Körper Wärme ab, so hat die von ihm ausgetauschte Wärme ein negatives Vorzeichen: Q<0.
Beispiel:
Erhöht sich die Temperatur von 1 g Wasser um 1 K, so erhält das Wasser die Wärmemenge
Q=+4, 186 J.
Kühlt sich 1 g Wasser um 1 K ab, so gibt das Wasser die Wärmemenge Q=−4, 186 J ab.
4.4
4.4.1
Wärme und Aggregatzustandänderung
Schmelzen und spezifische latente Schmelzwärme
Genau wie Eis (bei 0 ◦ C) schmilzt auch jeder andere Stoff (d.h. er geht vom festen in den flüssigen Aggregatzustand über) bei einer bestimmten Temperatur θS , seiner „Schmelztemperatur”.
In folgender Tabelle ist die Schmelztemperatur einiger gängiger Stoffe aufgelistet:
26
c Y. Reiser
4. KALORIMETRIE
Stoff
Helium
Luft
Ethanol
Quecksilber
Öl
Eis
Blei
Aluminium
Gold
Stahl
Eisen
Wolfram
Diamant
θS (◦ C)
-272
-220
-117
-39
∼-10
0
327
660
1064
1515
1535
3410
3540
Tabelle 4: Schmelztemperaturen
Wir haben gelernt, dass Wärmezufuhr zu einer Temperaturerhöhung eines Körpers führen kann.
Hat ein Körper jedoch seine Schmelztemperatur erreicht, so führt eine weitere Wärmezufuhr
nicht mehr zu einer Temperaturerhöhung. Die zugeführte Wärme wird jetzt genutzt, um den
Aggregatzustand des Körpers von fest auf flüssig umzuändern.
Erklärung :
Da die Teilchen eines festen Körpers auf der Stelle vibrieren, führt Wärmezufuhr dazu, dass
diese Vibrationen heftiger werden und somit die Temperatur des Körpers steigt. Beim Erreichen der Schmelztemperatur können die Teilchen nun plötzlich übereinander gleiten, da die
zusätzliche Energie jetzt ausreicht, um die Bindungen zwischen den Teilchen aufzulösen, die
alle Teilchen in der geordneten Gitterstruktur gehalten haben.
Die Wärmemenge Q , die benötigt wird, um eine Masse m eines Stoffs zu schmelzen, wird mit
folgender Formel berechnet:
Q = m · LS > 0
LS ist die spezifische, latente Schmelzwärme. Sie ist eine Eigenschaft eines jeden festen Stoffs.
J
Ihre Einheit ist kg
. Ihr Wert entspricht der Energie, die man 1 kg eines Stoffs auf seiner Schmelztemperatur zuführen muss, um ihn zu schmelzen.
J
)
LS ( kg
Stoff
Aluminium
Eisen
Eis
Quecksilber
Blei
396.000
267.000
330.000
11.000
25.000
Tabelle 5: Spez. latente Schmelzwärmen
27
c Y. Reiser
4. KALORIMETRIE
4.4.2
Erstarren
Jede Flüssigkeit erstarrt (d.h. wird fest) bei einer ganz bestimmten Temperatur. Diese Erstarrungstemperatur gleich der Schmelztemperatur θS . Während dem Erstarrungsvorgang gibt die
Flüssigkeit Wärme an ihre Umgebung ab.
Die Wärmemenge Q, die eine Flüssigkeit der Masse m während ihrer Erstarrung abgibt, wird
mit folgender Formel berechnet:
Q = −m · LS < 0
wobei LS die spez. latente Schmelzwärme ist.
4.4.3
Verdampfen und spezifische latente Verdampfungswärme
Wie Wasser verdampft/siedet auch jede andere Flüssigkeit (d.h. sie geht vom flüssigen in
den gasförmigen Zustand über) bei einer ganz bestimmten Temperatur, der Siedetemperatur/Verdampfungstemperatur θV . Folgende Tabelle listet die Siedetemperaturen einiger gängiger
Stoffe auf:
Stoff
Helium
Stickstoff
Sauerstoff
Propan
Butan
Ethanol
Wasser
Heizöl
Quecksilber
Aluminium
θV (◦ C)
-267
-196
-183
-45
1
78,5
100
210 bis 380
357
2467
Tabelle 6: Siedetemperaturen
Nach Erreichen der Siedetemperatur wird zusätzlich zugeführte Wärme ausschließlich dazu benutzt, den Aggregatzustand des Körpers von flüssig auf gasförmig umzuändern.
Die Wärme Q, die benötigt wird, um eine Flüssigkeit der Masse m in ein Gas umzuwandeln,
wird mit folgender Formel berechnet:
Q = m · LV > 0
LV ist die spez. latente Verdampfungswärme. Genau wie die spez. lat. Schmelzwärme ist sie
J
eine Eigenschaft eines jeden Stoffs. Auch diese Größe wird in der Einheit kg
angegeben. Sie
entspricht der Energie, die man 1 kg einer Flüssigkeit zuführen muss, damit sie sich vollständig
in Gas umwandelt.
28
c Y. Reiser
4. KALORIMETRIE
Stoff
J
)
LV ( kg
Eisen
Wasser
Ethanol
Kohlendioxid
Wasserstoff
Quecksilber
Sauerstoff
Stickstoff
Helium
6.310.000
2.300.000
850.000
590.000
452.000
300.000
213.000
200.000
25.000
Tabelle 7: Spez. latente Verdampfungswärme
4.4.4
Kondensieren
Jedes Gas wandelt sich bei seiner Kondensationstemperatur, die der Verdampfungstemperatur
θV entspricht, in eine Flüssigkeit um : es kondensiert. Während dieser Zustandsänderung gibt
das Gas Wärme an seine Umgebung ab.
Die Wärmemenge Q, die ein Gas der Masse m abgibt, wenn es kondensiert, kann mit folgender
Formel berechnet werden:
Q = −m · LV < 0
wobei LV die spez. latente Verdampfungswärme des Stoffs ist.
29
c Y. Reiser
4. KALORIMETRIE
4.5
Wärmezufuhr : Zusammenfassung
Betrachten wir einen festen Körper der Masse m, der sich zu Beginn auf einer Temperatur θinit.
befindet. Dem Körper wird nun kontinuierlich Wärme zugeführt.
θ(◦ C)
θf in.
θV
θF
θinit.
I
II
III
IV
V
Q(J)
Auf der Grafik (nicht maßstabgetreu) ist die Temperatur des Körpers dargestellt, nachdem er
eine bestimmte Wärmemenge erhalten hat.
− Phase I : die erhaltene Wärme wird genutzt, um die Temperatur bis zur Schmelztemperatur zu erhöhen : QI = m · cf est · (θS − θinit. )
− Phase II : die erhaltene Wärme wird genutzt, um den Körper zu schmelzen : QII = m · LS
− Phase III : die erhaltene Wärme wird dazu genutzt, die Temperatur der Flüssigkeit von
der Schmelztemperatur auf die Siedetemperatur zu erhöhen: QIII = m · cF l. · (θV − θS )
− Phase IV : die erhaltene Wärme wird genutzt, um den Körper zu verdampfen :
QIV = m · LV
− Phase V : die Wärme wird zur Temperaturerhöhung des Gases genutzt :
QV = m · cgaz · (θf in. − θV )
4.6
Kalorimeter
Ein Kalorimeter ist ein Gefäß mit quasi-adiabatischen Wänden, was dazu benutzt wird, ausgetauschte Wärmemengen zu messen. Der Wärmeaustausch kann zwischen mehreren enthaltenen
Körpern stattfinden. Dabei sind auch Aggregatzustandsänderungen möglich. Das Innere des
Kalorimeters stellt ein thermisch isoliertes System dar. Es gibt also weder Austausch von Materie, noch von Energie (Arbeit oder Wärme) zwischen dem Inhalt des Kalorimeters und der
30
c Y. Reiser
4. KALORIMETRIE
Aussenwelt.
Es lässt sich sich nicht vermeiden, dass die Innenwände des Kalorimeters am Wärmeaustausch
mit dem Inhalt teilnimmt. Deshalb hat jeder Kalorimeter eine bestimmte Wärmekapazität µ
(in J/K angegeben) : die Wärmekapazität des Kalorimeters entspricht numerisch der Wärmemenge, die der Kalorimeter austauscht, wenn seine Temperatur um 1 K (oder 1 ◦ C) verändert
wird.
Ändert die Temperatur eines Kalorimeters um den Wert ∆T , so ist die von ihm abgegebene/erhaltene Wärmemenge gleich:
Q = µ · ∆T
4.7
Mischungen
Beispiel : Bestimmen der spez. Wärmekapazität eines unbekannten Körpers
Eine Masse m1 einer Flüssigkeit der spez. Wärmekapazität c1 und einer Temperatur θ1 wird in
einen Kalorimeter der Wärmekapazität µ gegeben (nach kurzer Zeit kann angenommen werden,
dass die Ausgangstemperatur des Kalorimeters ebenfalls θ1 ist). Anschließend wird ein Körper
der Masse m2 und einer Temperatur θ2 > θ1 dazu gemischt. Die spez. Wärmekapazität c2 dieses
Körpers ist unbekannt.
Nach kurzer Zeit beträgt hat Temperatur der sich im thermischen Gleichgewicht befindlichen
Mischung (Kalorimeter + Flüssigkeit + unbek. Körper) den Wert θM .
− vom Kalorimeter erhaltene Wärme:
Q0 = µ · ∆T0 = µ · (θM − θ1 )
− von der Flüssigkeit erhaltene Wärme:
Q1 = m1 · c1 · ∆T1 = m1 · c1 · (θM − θ1 )
− vom unbekannten Körper abgegebene Wärme:
Q2 = m2 · c2 · ∆T2 = m2 · c2 · (θM − θ2 )
Da der Kalorimeter keinen Wärmeaustausch mit der Umgebung zulässt, werden die Wärmen
nur von den unterschiedlichen Körpern der Mischung untereinander ausgetauscht und es gilt
die thermische Gleichung:
Q0 + Q1 + Q2 = 0
⇔ µ · (θM − θ1 ) + m1 · c1 · (θM − θ1 ) + m2 · c2 · (θM − θ2 ) = 0
⇔ m2 · c2 · (θM − θ2 ) = −µ · (θM − θ1 ) − m1 · c1 · (θM − θ1 )
1 )−m1 · c1 · (θM −θ1 )
⇔
c2 = −µ · (θM −θ
m2 · (θM −θ2 )
31
c Y. Reiser
5. GASGESETZE
5
5.1
Gasgesetze
Zustandsgrößen
Druck p, Volumen V und Temperatur T einer eingeschlossenen Gasmenge hängen eng miteinander zusammen und werden als Zustandsgrößen bezeichnet.
Wir werden im folgenden zuerst untersuchen, wie zwei der drei Zustandsgrößen miteinander
zusammenhängen, wenn die dritte Größe jeweils konstant bleibt,
Anschließend leiten wir daraus den Zusammenhang aller drei Größen zusammen ab.
5.2
5.2.1
Gasgesetze bei einer konstanten Zustandsgröße
Gesetz von Gay-Lussac
Versuch:
Wie auf der Zeichnung zu sehen schliesst der Wassertropfen im Glasröhrchen die Luft in einem
Kolben ein. Die Lefttemperatur T im Kolben kann durch Erwärmen des Wasserbads allmählich
erhöht werden. Man kann beobachten, dass das Volumen V ebenfalls größer. Der Druck p im
Innern ist stets gleich dem Umgebungsdruck, also konstant, da sich die Gasmenge im Gefäß
frei ausdehnen kann.
20,0
∆T
K
∆V
Abbildung 14: Versuch: Gesetz von Gay-Lussac
32
c Y. Reiser
5. GASGESETZE
Werden die absolute Temperatur und das Volumen in ein Diagramm eingetragen, so stellt man
fest, dass die Messpunkte (von Messfehlern abgesehen) auf einer Geraden liegen. Verlängert
man diese Gerade nach tieferen Temperaturen, so verläuft sie durch den Koordinatenursprung:
es ist eine Nullpunktgerade.
Daraus schließen wir:
Gesetz von Gay-Lussac3 :
Wenn der Druck einer eingeschlossenen Gasmenge konstant bleibt, ist ihr Volumen
proportional zur Temperatur:
p konstant :
Da V ∼ T ist, gilt auch :
V
T
V ∼T
= konstant.
Hat ein Gas bei einem konstanten Druck p bei einer Temperatur T1 ein Volumen V1 und bei
einer Temperatur T2 ein Volumen V2 , so gilt:
V2
V1
=
T1
T2
⇐⇒
V2
T2
=
V1
T1
Beispiele:
− Stülpt man einen Ballon über die Öffnung eines Glaskolbens, so füllt sich der Ballon bei
Erwärmung des Kolbens schnell mit Luft. Der Druck im Ballon entspricht dabei immer
noch etwa dem Umegbungsdruck.
− Füllt man mit einem Föhn heisse Luft in eine Plastikflasche, die man dann sofort verschliesst und anschließend abkühlen läßt, so zieht sich die Flasche stark zusammen. Der
Druck in der Flasche ist annähernd gleich dem Druck der Umgebungsluft.
− ...
3
Das Gesetz wurde erstmals 1802 von Joseph Louis Gay-Lussac(1778-1850 formuliert), einem französischen
Chemiker und Physiker
33
c Y. Reiser
5. GASGESETZE
5.2.2
Gesetz von Amontons
20,0
Manometer
∆T
K
Abbildung 15: Versuch: Gesetz von Amontons
In diesem Versuch wird ein mit Luft gefüllter Kolben erwärmt. Da die Luft sich nicht ausdehnen
kann, ist ihr Volumen konstant.
Stellt man den Druck p der eingeschlossenen Luft zur absoluten Temperatur T auf einer Grafik
dar, so stellt man fest, dass die Messwerte (von Messfehlern abgesehen) auf einer Nullpunktgeraden liegen.
Daraus schließen wird:
Gesetz von Amontons4 :
Wenn das Volumen einer eingeschlossenen Gasmenge konstant bleibt, dann ist ihr Druck
proportional zur Temperatur:
V konstant :
4
p∼T
Das Gesetz wurde erstmals von dem franz. Naturwissenschaftler Guillaume Amontons(1663-1705) formu-
liert
34
c Y. Reiser
5. GASGESETZE
Da p ∼ T ist, gilt auch:
p
T
= konstant.
Hat ein Gas bei einem konstanten Volumen bei einer Temperatur T1 einen Druck p1 und bei
einer Temperatur p2 einen Druck p2 , so gilt:
p1
p2
=
T1
T2
p2
T2
=
p1
T1
⇐⇒
Beispiele:
− Luftdruckfeuerzeug
− Luft in einem Autoreifen
− Der Druck in einer stark erwärmten Deodose kann soweit ansteigen, dass sie explodiert
− ...
5.2.3
Gesetz von Boyle und Mariotte
Drückt man den Kolben einer Fahrradpumpe sehr langsam in die Pumpe hinein, so wird sich
die Pumpe kaum erwärmen. Auch das Luftdruckfeuerzeug funktioniert nur bei sehr schnellem
Zusammendrücken (da bei langsamer Geschwindigkeit die Temperatur konstant bleibt). Bei
langsamen Zusammendrücken bleibt die Temperatur also konstant, und es gilt das
Gesetz von Boyle und Mariotte5 :
Bleibt die Temperatur einer eingeschlossenen Gasmenge konstant, dann ist ihr Volumen
umgekehrt proportional zu ihrer Temperatur:
T konstant :
Wenn p ∼
1
V
ist, dass gilt auch:
p
1
V
= konstant
p∼
⇔
1
V
p · V = konstant.
Hat ein Gas bei konstanter Temperatur bei einer Druck p1 ein Volumen V1 und bei einem Druck
p2 ein Volument V2 , so gilt:
p1 · V 1 = p2 · V 2
5
Dieses Gesetz wurde erstmals 1862 von dem britischen Chemiker und Physiker Robert Boyle(1627-1691)
und, unabhängig davon, einige Jahre später von dem franz. Forscher Edmé Mariotte(1620-1684) formuliert.
35
c Y. Reiser
5. GASGESETZE
5.3
Allgemeines Gasgesetz
Pumpt man Luft in einen Reifen, so ändert sich nicht nur der Druck der hineingepumpten Luft,
sondern wir verringern gleichzeitig ihr Volumen und erhöhen ihre Temperatur.
Zu Beginn hat die Luft in der Pumpe das Volumen V1 , die Temperatur T1 und den Druck p1 .
Nachdem Einschieben des Kolbens hat diese Luft nun das Volumen V2 , die Temperatur T2 und
den Druck p2 .
Die Zustandsgrößen der Luft haben sich also von p1 , V1 , T1 nach p2 , V2 , T2 verändert.
Gedankenexperiment:
Die Zustandsänderung der Luft von p1 , V1 , T1 nach p2 , V2 , T2 wäre theoretisch auch in zwei
Einzelschritten möglich:
1. Wir verringern das Volumen von V1 auf V2 , indem das Gas auf eine Zwischentemperatur
Tzw. abgekühlt wird. Der Druck bleibt dabei konstant. Hier gilt also das Gesetz von GayLussac (s. S. 33):
V2
Tzw.
=
V1
T1
⇔ Tzw. = T1 ·
Stopfen
V2
V1
(1)
Wärme
V2 , Tzw. , p2
Abbildung 16: Gedankenexperiment: 1. Schritt
2. Nun wird der Druck von p1 auf p2 erhöht, indem die Temperatur bei konstantem Volumen
von Tzw. auf T2 erhöht wird. Hier gilt nun das Gesetz von Amontons(s. S. 34):
T2
p2
=
p1
Tzw.
⇔ Tzw. = T2 ·
36
p1
p2
(2)
c Y. Reiser
5. GASGESETZE
Stopfen
V2 , T2 , p2
Wärme
Abbildung 17: Gedankenexperiment: 2. Schritt
Kombiniert man die beiden Gleichungen (1) und (2), so erhält man:
T1 ·
V2
p1
= T2 ·
V1
p2
⇔ p1 ·
V1
V2
= p2 ·
T1
T2
Zustandsgleichung für das ideale Gas (auch allgemeines Gasgesetz genannt):
Hat eine bestimmte Menge Gas zu Beginn ein Volumen V1 , eine Temperatur T1 , einen Druck
p1 und zum Schluss hat das Volumen den Wert V2 , die Temperatur den Wert T2 und der
Druck den Wert p2 , dann gilt:
V2
V1
= p2 ·
p1 ·
T1
T2
Für eine bestimmte Gasmenge gilt also allgemein:
p·
V
= konstant
T
37
c Y. Reiser