Einführung in die Physik I Wärme 1

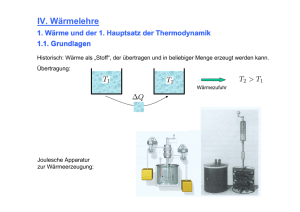
Einführung in die Physik I
Wärme 1 - Grundlagen
O. von der Lühe und U. Landgraf
Wärme und Temperatur
• Wärme ist eine Form von
Energie, die ausgedehnten
Körpern zu eigen ist
• Wärmeenergie besteht aus der
kinetischen Energie der
ungeordneten Bewegung von
Bestandteilen ausgedehnter
Körper
• Kinetische Energie wird über
Stöße und Fernwirkung
zwischen den Teilchen
ausgetauscht
• Die Temperatur ist ein lineares
Maß der mittleren kinetischen
Energie der Teilchen
Wärme 1
Ideales Gas: Teilchen
bewegen sich unabhängig,
Wechselwirkung nur bei
Stößen von Teilchen
Gleichverteilungssatz:
im Mittel ist die
kinetische Energie für
jedes Teilchen dieselbe
2
1
Definition der Temperatur
•
Allgemein:
– Bei einer Temperatur T beträgt die
mittlere kinetische Energie pro
Freiheitsgrad eines Teilchens
•
Einatomiges Gas:
– Mittlere kinetische Energie jedes
Teilchens (3 FG)
•
Zweiatomiges Gas (z. B. Luft):
– Mittlere kinetische Energie und
Rotationsenergie (5 FG)
•
Mehratomige Gase und Festkörper:
•
Einheit der Temperatur:
Kelvin [K]
•
Boltzmann-Konstante k
EFG =
1
⋅ k ⋅T
2
Ekin =
1
3
⋅ m ⋅ v2 = ⋅ k ⋅T
2
2
Etrans + rot =
Ekin =
(
)
1
5
⋅ m ⋅ v2 + J ⋅ω 2 = ⋅ k ⋅T
2
2
1
6
⋅ m ⋅ v 2 + Epot = ⋅ k ⋅ T
2
2
[
k = 1.381⋅10 −23 J K -1
]
Wärme 1
3
Temperaturskala
• Es gibt eine absoluten Nullpunkt der
Temperaturskala, welcher der mittleren
Energie von Null entspricht
• Kein Körper kann eine Temperatur kleiner
als 0 [K] haben!
• Eine praktische Temperaturskala ist die
Celsius-Skala mit den Fixpunkten 0 °C
und 100 °C (Gefrier- und Siedepunkt des
Wassers bei einem Druck von 1.013 [bar])
• Ein Temperaturunterschied von 1 [K]
entspricht 1 °C
• Eine andere in den USA gebräuchliche
Temperaturskala ist Fahrenheit (°F)
Wärme 1
1[K ] ≡ 1°C
0 [K ] = − 273,2 °C
0 °C = 32 °F
100 °C = 212 °F
4
2
Wärmeenergie - Beispiel
• Luft hat eine Wärmekapazität von 710 [J kg-1 K-1]
• Bei temperaturunabhängiger Wärmekapazität ergibt sich bei einer
Temperatur von 300 [K] (= 27 °C) ein Wärmeenergieinhalt von
710 · 300 = 213.000 [J] pro Kilogramm Luft
• Luftmoleküle sind i. d. R. zweiatomig. Es entfallen drei
Freiheitsgrade für die Translation und zwei Freiheitsgrade für dir
Rotation
• Pro Kilogramm erhält man damit 3/5 · 213 [kJ] = 128 [kJ] kinetische
Energie
1
2 Ekin
Ekin = mv 2 → v =
m
2
• v = (256.000)½ = 505 [m s-1]
Wärme 1
5
Thermometer
• Messbare Größen, die reproduzierbar
von der Temperatur abhängen,
können für Thermometer verwendet
werden
– Thermische Ausdehnung von
Flüssigkeiten und Festkörpern
– Temperaturabhängigkeit des
elektrischen Widerstands
– Direkte Messung der mittleren
Geschwindigkeit der Teilchen
(optischer Dopplereffekt)
– Strahlungsleistung
• Eichung durch Fixpunkte
Wärme 1
l = l0 (1 + α ⋅ T ) V = V0 (1 + γ ⋅ T ) γ = 3α
Lin. Ausdehnungskoeffizient
α / 10-6 [K-1] bei 100 °C
Quarzglas
Jenaer Glas
Eisen
Kupfer
Aluminium
Blei
NaCl
0.510
8.1
12.0
16.7
23.8
29.4
40.0
Raumausdehnungskoeffizient
γ / [K-1] bei 18 °C
Aceton
Benzol
Quecksilber
0.00143
0.00106
0.00018
6
3
Wärmekapazität
• Erwärmt man einen Körper, so
muss man ihm Energie zuführen.
Die Wärmekapazität ist die
Menge von Energie, die eine
Stoffmenge zur Erhöhung der
Temperatur um 1 [K] benötigt
• Die Energiezunahme pro Teilchen
ist bei f Freiheitsgraden bei einer
Temperaturänderung von ΔT
f
k ⋅ ΔT
2
ΔETeilchen =
ΔEmol = N A ⋅
• Die Energiezunahme pro mol ist
• Die Energiezunahme pro kg ist
ΔE =
– rel. Atomgewicht μ
– Masse des Wasserstoffatoms mH
f
k ⋅ ΔT
2
f
k ⋅ ΔT
2 ⋅ μ ⋅ mH
Wärme 1
7
Wärmekapazität
[
• Molare Wärmekapazität C
C=
f
ΔEmol
= N A ⋅ ⋅ k J mol-1 K -1
2
ΔT
• Spezifische Wärmekapazität
c=
ΔE
f ⋅k
=
ΔT 2 ⋅ μ ⋅ mH
• Festkörper: f = 6
(Dulong–Petit‘sche Regel)
C = 3 N A k = 24.9 J mol-1 K -1
[
[J kg
-1
K -1
]
]
]
Wärmekapazität von Wasser:
cH2O = 4185 [J kg-1 K-1]
Für eine Temperaturerhöhung
von 1g Wasser um 1 °C
braucht man eine Energie von
4.185 [J] = 1 [cal] Kalorie
Wärme 1
8
4