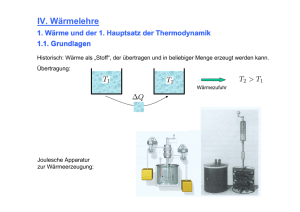
Spezifische Wärme Q cm T

∆Q = c ⋅ m ⋅ ∆T
Spezifische Wärme
Allgemein:
Die spezifische Wärmekapazität c (kurz "spezifische Wärme") ist ein Maß für die Wärmeenergie ∆Q, die
benötigt wird, um 1 kg eines Stoffes um 1 K zu erwärmen. Die spezifische Wärmekapazität c ist materialabhängig und gilt nicht über Phasengrenzen hinweg.
Beispiel:
Wasser :
c w = 4,19
kJ
kg ⋅ K
spezifische
Wärmekapazität
Bedeutet: Wird 1 kg Wasser eine Energie von ca. 4190 Joule
zugeführt, so erhöht sich die Wassertemperatur um 1 K.
Masse
∆Q > 0 : System nimmt Wärme von außen auf,
∆Q = c ⋅ m ⋅∆T
Wärmeenergie
Temperaturänderung
∆Q > 0 : System gibt Wärme nach außen ab
Für Gase gibt es die spezifische Wärmekapazität cP (Druck konstant) und cV (Volumen konstant).
Siehe Seite 3
∆Q = c ⋅ m ⋅ ∆T
Spezifische Wärme
Versuch: „Spezifische Wärmekapazität von Metallen“
Versuch:
Bei diesem Versuch wurden vier Metallstücke (Al, Fe, Cu, Pb) mit gleicher Masse m, in kochendem
Wasser erhitzt und dann in Bechergläser mit kaltem Wasser (Raumtemperatur TR) gegeben. Anschließend
wurde die Wassertemperatur T1 in allen vier Bechergläsern gemessen.
m = 0,10 kg
mw = 0,35 kg
cw = 4,19 kJ/kgK
TR = 20,5 °C
T0 = 100 °C
Temperatur T1
Dichte ρ
(bei 20 °C)
spezifische
Wärmekapazität c
25,2 °C
2,70 g/cm³
22,9 °C
7,87 g/cm³
22,6 °C
8,92 g/cm³
21,2 °C
11,34 g/cm³
0,39 kJ/kgK
0,13 kJ/kgK
Dichte
0,92 kJ/kgK
0,46 kJ/kgK
spezifische Wärmekapazität
1. Hauptsatz der Thermodynamik
∆U = Q + W
Spezifische Wärmekapazität bei Gasen:
Die spezifische Wärmekapazität von Gasen hängt von den äußeren Bedingungen ab. Es wird zwischen der
spezifischen Wärmekapazität cV bei konstantem Volumen (isochorer Prozess) und der spezifischen
Wärmekapazität cP bei konstantem Druck (isobarer Prozess) unterschieden.
isochorer Prozess: Die gesamte Wärmeenergie wird komplett zur Änderung der Temperatur des Gases genutzt.
D.h. die Änderung der inneren Energie ∆U des Systems erfolgt allein durch die Wärmemengenänderung ∆Q.
∆U = ∆Q mit ∆Q = c V ⋅ m ⋅∆T
isobarer Prozess: Bei diesem Prozess wird ein Teil der Wärmeenergie zur Verrichtung von Volumenarbeit
genutzt, da sich Gase beim Erwärmen ausdehnen muss, wenn der Druck konstant bleiben
soll. Die restliche Wärme wird für die Temperaturerhöhung genutzt.
D.h. die Änderung der inneren Energie ∆U des Systems erfolgt durch Volumenarbeit ∆W
und durch Wärmeänderung ∆Q.
∆U = ∆Q + ∆W mit ∆Q = c P ⋅ m ⋅ ∆T und ∆W = − p ⋅ ∆V
Bei isobaren Zustandsänderungen muss mehr Wärmeenergie zugeführt werden um ein Gas um 1 K zu
erwärmen als bei isochoren Zustandsänderungen.
cP > cV