Anwendung der Formel der totalen Wahrscheinlichkeit Beispiel 3.13

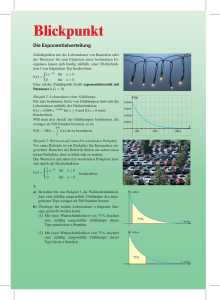
Anwendung der Formel der totalen Wahrscheinlichkeit
Beispiel 3.13:
- Produktion von Glühlampen auf 4 Maschinen M1 , M2 , M3 und M4
- Anteile an der Gesamtproduktion: 10%, 20%, 30% und 40%
- Ausschussanteile: 2%, 1%, 4% und 2%
- zufällige Entnahme einer Glühlampe, Prüfung auf Funktionstüchtigkeit
Mit welcher Wahrscheinlichkeit zieht man dabei eine defekte Glühlampe?
0.4
0.3
A4
A3
0.02
0.04
0
B
0.2
0.1
A2
A1
0.01
0.02
Ereignisse:
Ai : Die zufällig entnommene Glühlampe wurde auf
der Maschine Mi produziert.
B : Die der Gesamtproduktion entnommene
Glühlampe ist defekt.
Das Ereignis B ist über die ”Zwischenstationen”
A1 , A2 , A3 und A4 zu erreichen.
Mit Hilfe des (unvollständigen) Ereignisbaumes erhält man:
P (A1 )·P (B|A1 ) = 0.1·0.02 = 0.002 ,
P (A2 )·P (B|A2 ) = 0.2·0.01 = 0.002 ,
P (A3 )·P (B|A3 ) = 0.3·0.04 = 0.012 ,
P (A4 )·P (B|A4 ) = 0.4·0.02 = 0.008,
und mittels der Formel der totalen Wahrscheinlichkeit (mit n = 4) ergibt sich:
4
X
P (B) =
P (Ai ) · P (B|Ai ) = 0.002 + 0.002 + 0.012 + 0.008 = 0.024 .
i=1
Mathematik III - Folie 39
Stetige und diskrete Zufallsvariable (ZV)
Definition 14.1:
Unter einer Zufallsvariablen (oder Zufallsgröße) X versteht man eine Abbildung,
die jedem Elementarereignis ω aus der Ergebnismenge Ω eines Zufallsexperiments
genau eine reelle Zahl X(ω) zuordnet.
Eine ZV heißt dabei diskret, wenn sie nur endlich viele oder abzählbar unendlich
viele reelle Werte annehmen kann.
Eine ZV heißt stetig, wenn sie jeden beliebigen Wert aus einem (reellen) endlichen
oder unendlichen Intervall annehmen kann.
Beispiel 14.1:
a) fünfmaliges Würfeln mit einem homogenen Würfel, dabei feststellen
wie oft die Augenzahl ”6” auftritt
⇒ X = Anzahl von Würfen mit der Augenzahl ”6”
ist eine diskrete ZV mit den möglichen Werten 0, 1, 2, 3, 4 oder 5
b) Anzahl X der Atome, die in einem bestimmten Zeitintervall in einer radioaktiven Substanz zerfallen
⇒ diskrete ZV mit den abzählbar unendlich vielen Werten 0, 1, 2, . . .
c) Herstellung einer großen Stückzahl von Zylinderscheiben mit einem
vorgeschriebenen Durchmesser von 5 mm, zufallsbedingte Abweichungen
von diesem Sollwert
⇒ Durchmesser X einer solchen Scheibe kann als stetige ZV
aufgefasst werden (mit Werten aus einem bestimmten Intervall)
Mathematik III - Folie 40
Dichtefunktion und Verteilungsfunktion einer stetigen ZV
Beispiel 14.2:
Die Funktionsdauer T eines elektronischen Bauelements ist eine stetige ZV.
Die zugehörige Dichtefunktion sei (Maßeinheit: Stunden)
0
für t < 0
f (t) =
0.002e−0.002t für t ≥ 0 .
(Diese Funktion besitzt tatsächlich die Eigenschaften einer Dichtefunktion,
Z∞
denn f (t) ≥ 0 und
f (t) dt = 1.)
−∞
Dann gilt für t ≥ 0:
Zt
Zt
f (u) du = 0.002 ·
F (t) =
−∞
e−0.002u du = 1 − e−0.002t
0
Aus der Kenntnis der Verteilungsfunktion F (t) lässt sich z.B. berechnen,
mit welcher Wahrscheinlichkeit das Bauelement spätestens bei Erreichen
der 1000-Stunden-Betriebsgrenze ausfällt:
P (T ≤ 1000) = F (1000) = 1 − e−0.002·1000 = 1 − e−2 = 0.865 .
Mathematik III - Folie 41