Blickpunkt

Blickpunkt
Die Exponentialverteilung
Zufallsgrößen wie die Lebensdauer von Bauteilen oder
die Wartezeit bis zum Eintreten eines bestimmten Ereignisses lassen sich häufig mithilfe einer Dichtefunktion f von folgendem Typ beschreiben:
l elx
|fflffl{zfflffl}
f(x) ¼
für x 0
0
für x < 0
Eine solche Zufallsgröße heißt exponentialverteilt mit
Parameter l (l > 0).
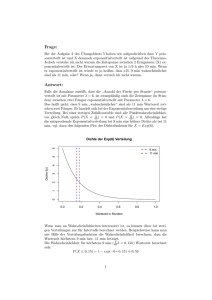
Beispiel 1: Lebensdauer einer Glühlampe
Für eine bestimmte Sorte von Glühlampen lässt sich die
Lebensdauer mithilfe der Dichtefunktion
f(x) ¼ 0,004 e0,004x für x 0 und f(x) ¼ 0 sonst
beschreiben.
Will man den Anteil der Glühlampen bestimmen, die
weniger als 300 Stunden brennen, so ist
300
Ð
f(x) dx zu berechnen.
P(X < 300) ¼
0
Beispiel 2: Wartezeit auf einen frei werdenden Parkplatz
Vor einer Behörde ist ein Parkplatz für Kurzparker eingerichtet. Besucher der Behörde finden nie sofort einen
freien Parkplatz, aber es lohnt sich zu warten.
Die Wartezeit auf einen frei werdenden Parkplatz lasse
sich durch die Dichtefunktion
|fflfflfflffl{zfflfflfflffl}
f(x) ¼
1 12 x
e
2
für x 0
0
für x < 0
beschreiben.
1.
a) Berechne für das Beispiel 1 die Wahrscheinlichkeit,
dass eine zufällig ausgewählte Glühlampe des angegebenen Typs weniger als 300 Stunden brennt.
b) berlege, für welche Lebensdauer x folgende Aussage gemacht werden kann:
(1) Mit einer Wahrscheinlichkeit von 75% leuchtet
eine zufällig ausgewählte Glühlampe dieses
Typs mindestens x Stunden.
(2) Mit einer Wahrscheinlichkeit von 75% leuchtet
eine zufällig ausgewählte Glühlampe dieses
Typs bis zu x Stunden.
Die Exponentialverteilung
199
2.
Die Lebensdauer eines bestimmten elektronischen Bauteils lasse sich mithilfe einer Dichtefunktion f
1 x
100
1
e
mit f(x) ¼ 100
für x 0 und f(x) ¼ 0 sonst beschreiben.
a) Welche mittlere Lebensdauer hat das Bauteil? Bestimme dazu den Erwartungswert der zugehöri1
Ð
gen Zufallsgröße: E(X) ¼ x f(x) dx.
0
b) Zeige, dass allgemein für eine exponentialverteilte Zufallsgröße x gilt:
Ist f die Dichtefunktion einer exponentialverteilten Zufallsgröße mit Parameter l, dann gilt für den
Erwartungswert: E(X) ¼ m ¼ 1l .
3.
a) Zeige, dass man im Beispiel 2 im Mittel 2 Zeiteinheiten (Minuten) auf einen freien Parkplatz warten muss.
b) Mit welcher Wahrscheinlichkeit hat man nach spätestens 5 Minuten einen Parkplatz gefunden?
4.
Beweise, dass durch f(x) ¼ l elx für x 0 und f(x) ¼ 0 sonst tatsächlich eine Dichtefunktion f im
Sinne der Definition von Seite 193 gegeben ist.
TAB
5.
Bestimme eine geeignete Dichtefunktion zu den folgenden Messreihen. Benutze ggf. die Möglichkeit
mithilfe einer Tabellenkalkulation eine möglichst gut „passende“ Exponentialfunktion zu finden.
(1) 300 Glühbirnen wurden einem Dauertest un- (2) 200 elektronische Bauteile wurden überprüft.
terzogen. Es ergaben sich folgende Messergebnisse:
Zeitdauer
Anzahl der
Zeitdauer
Anzahl der
in h
funktionierenden
in h
funktionierenden
Glühlampen
Bauteile
0
300
0
200
40
243
20
170
80
207
40
141
120
164
60
113
160
137
80
90
200
112
100
70
240
95
120
54
280
79
140
47
320
62
160
39
360
51
180
32
400
43
200
25
440
34
220
20
480
29
240
16
520
27
260
14
560
23
280
11
600
19
300
10
640
18
320
9
680
14
340
8
720
10
760
7
800
5
Die Exponentialverteilung
200
6.
a) Zeige, dass für die Varianz einer exponentialverteilten Zufallsgröße X mit Parameter l gilt:
V(X) ¼ s2 ¼ 12
l
b) Bestimme die Wahrscheinlichkeit, dass die Lebensdauer eines Bauteils
(1) höchstens m Zeiteinheiten dauert,
(2) höchstens m þ 1s beträgt.
7.
Jemand versucht, einen Freund telefonisch zu erreichen. Da dieser Freund häufig telefoniert, wundert
es nicht, dass der Anschluss besetzt ist; erfahrungsgemäß hat man im Mittel nach 10minütiger Wartezeit Erfolg und kommt durch. Die Wartezeit sei exponentialverteilt.
Mit welcher Wahrscheinlichkeit ist die Leitung
(1) bereits nach 5 Minuten,
(2) erst nach 20 Minuten frei?
8.
Bei einem häufig frequentierten Parkhaus wartet man Freitag nachmittags im Mittel 30 sec., bis ein
Platz frei wird. Die Wartezeit sei als exponentialverteilt angenommen.
Mit welcher Wahrscheinlichkeit
(1) muss man mehr als 30 sec. warten,
(2) ist ein Parkplatz nach spätestens 1 Minute frei?
9.
Eine Glühbirne (deren Lebensdauer exponentialverteilt sei) brenne mit Wahrscheinlichkeit 90% mindestens 200 Stunden (Sicherheitsgarantie des Herstellers).
a) Wie groß ist die mittlere Brenndauer der Glühbirne?
b) Mit welcher Wahrscheinlichkeit brennt sie auch noch nach 500 Stunden?
c) Wie lange kann die Glühbirne in 95% der Fälle genutzt werden?
10.
Die Lebensdauer eines elektronischen Bauteils betrage im Mittel 20 Monate.
Bestimme den Zeitpunkt tm so, dass P(X > tm) ¼ P(X tm) ¼ 50%.
11.
In einem Gerät arbeiten unabhängig 4 Bauteile, deren mittlere Lebensdauer jeweils 12 Monate beträgt. Das Gerät kann noch benutzt werden, wenn 3 der 4 Bauteile funktionieren.
Mit welcher Wahrscheinlichkeit kann man das Gerät nach
(1) 6 Monaten, (2) 12 Monaten, (3) 24 Monaten noch benutzen?
Anleitung: Bestimme die gesuchten Wahrscheinlichkeiten zunächst für jedes einzelne Bauteil und betrachte dann die binomialverteilte Zufallsgröße X: Anzahl der funktionierenden Bauteile.
12.
Ein Bauteil habe eine mittlere Lebensdauer von 6 Monaten.
(1) Bestimme die Wahrscheinlichkeit, dass das Bauteil noch nach 2 Monaten funktioniert.
(2) Das Bauteil wird bereits 1 Monat lang benutzt. Mit welcher Wahrscheinlichkeit wird es noch zwei
weitere Monate funktionieren?
Welche idealisierte Annahme liegt der Rechnung zugrunde?
13.
Eine Zufallsgröße sei exponentialverteilt mit dem Parameter l.
Mit welcher Wahrscheinlichkeit nimmt die Zufallsgröße Werte an, die größer sind
(1) als m, (2) als 2m, (3) als 3m?