Blatt 5 / Aufgabe 2

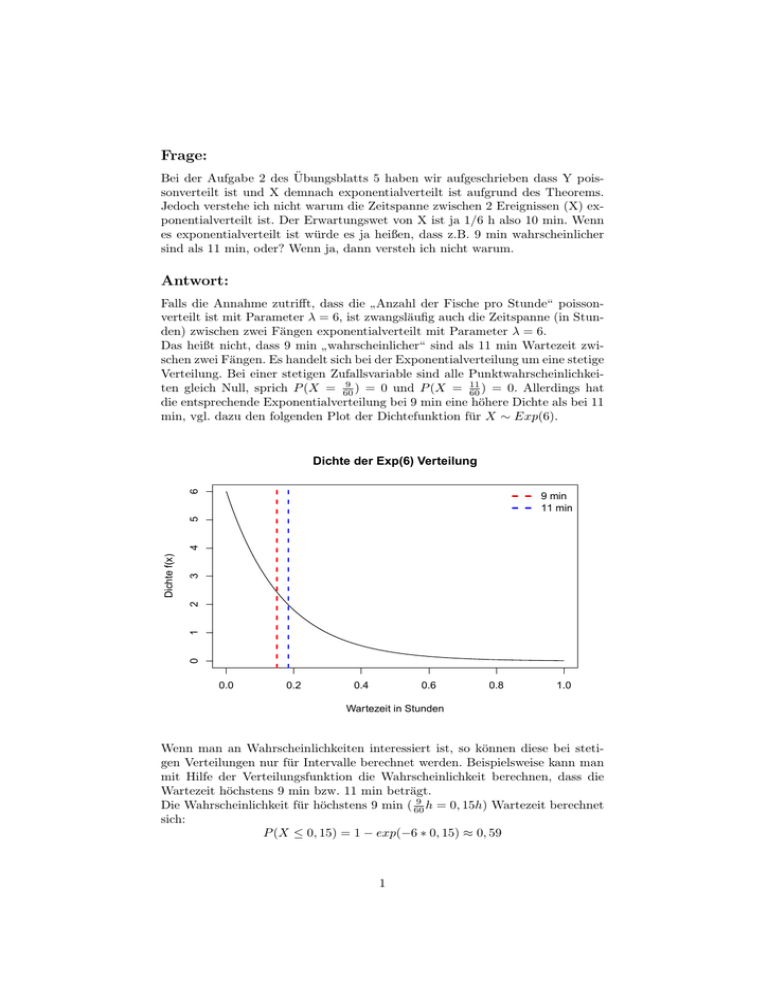
Frage:
Bei der Aufgabe 2 des Übungsblatts 5 haben wir aufgeschrieben dass Y poissonverteilt ist und X demnach exponentialverteilt ist aufgrund des Theorems.
Jedoch verstehe ich nicht warum die Zeitspanne zwischen 2 Ereignissen (X) exponentialverteilt ist. Der Erwartungswet von X ist ja 1/6 h also 10 min. Wenn
es exponentialverteilt ist würde es ja heißen, dass z.B. 9 min wahrscheinlicher
sind als 11 min, oder? Wenn ja, dann versteh ich nicht warum.
Antwort:
Falls die Annahme zutrifft, dass die Anzahl der Fische pro Stunde“ poisson”
verteilt ist mit Parameter λ = 6, ist zwangsläufig auch die Zeitspanne (in Stunden) zwischen zwei Fängen exponentialverteilt mit Parameter λ = 6.
Das heißt nicht, dass 9 min wahrscheinlicher“ sind als 11 min Wartezeit zwi”
schen zwei Fängen. Es handelt sich bei der Exponentialverteilung um eine stetige
Verteilung. Bei einer stetigen Zufallsvariable sind alle Punktwahrscheinlichkei9
) = 0 und P (X = 11
ten gleich Null, sprich P (X = 60
60 ) = 0. Allerdings hat
die entsprechende Exponentialverteilung bei 9 min eine höhere Dichte als bei 11
min, vgl. dazu den folgenden Plot der Dichtefunktion für X ∼ Exp(6).
6
Dichte der Exp(6) Verteilung
3
0
1
2
Dichte f(x)
4
5
9 min
11 min
0.0
0.2
0.4
0.6
0.8
1.0
Wartezeit in Stunden
Wenn man an Wahrscheinlichkeiten interessiert ist, so können diese bei stetigen Verteilungen nur für Intervalle berechnet werden. Beispielsweise kann man
mit Hilfe der Verteilungsfunktion die Wahrscheinlichkeit berechnen, dass die
Wartezeit höchstens 9 min bzw. 11 min beträgt.
9
Die Wahrscheinlichkeit für höchstens 9 min ( 60
h = 0, 15h) Wartezeit berechnet
sich:
P (X ≤ 0, 15) = 1 − exp(−6 ∗ 0, 15) ≈ 0, 59
1
Die Wahrscheinlichkeit für höchstens 11 min ( 11
60 h = 0, 183h) Wartezeit berechnet sich:
P (X ≤ 0, 183) = 1 − exp(−6 ∗ 0, 183) ≈ 0, 67
Man kann also davon ausgehen dass mit einer Wahrscheinlichkeit von 57% innerhalb von 9 min ein Fisch gefangen wird und mit einer Wahrscheinlichkeit
von 67% ein Fisch innerhalb von 11 min gefangen wird.
0.6
0.4
0.2
9 min
11 min
0.0
Verteilungsfkt. F(x)
0.8
1.0
Verteilungsfkt. der Exp(6) Verteilung
0.0
0.2
0.4
0.6
Wartezeit in Stunden
2
0.8
1.0