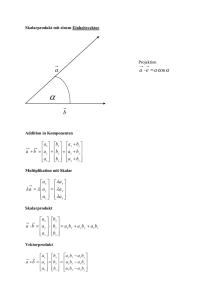
Skriptum Tragwerkslehre 1
Werbung

Tragwerkslehre I Statik Ausgabe: September 2013 Dipl.-Ing. E. Schuler Tragwerkslehre 1! 1 1. Einführung! 2 1.1. Die Statik als Teilgebiet der Mechanik! 2 1.2. Sicherheit! 3 1.3. Modellbildung! 4 1.4. Methoden der Statik! 4 2. Kräfte ! 5 2.1. Definition! 5 2.2. Arten von Kräften bzw. Lasten im Bauwesen! 5 2.3. Lehrsätze über Kräfte! 7 2.4. Das zentrale Kräftesystem! 8 2.5. Das allgemeine ebene Kräftesystem! 3. Schwerpunktsberechnungen! 10 19 3.1. Schwerpunkt von Linienzügen! 19 3.2. Schwerpunkt von Flächen! 20 3.3. Schwerpunkt symmetrischer Flächen und Linienzüge! 21 4. Ebene Stabwerke! 22 4.1. Äußere Standsicherheit - Ermittlung der Auflagerreaktionen! 4.2. Innere Standsicherheit - Ermittlung der inneren Kräfte (Schnittgrößen)!27 5. Besondere Tragwerke ! 22 32 5.1. Schräge Träger! 32 5.2. Geknickte Träger! 33 5.3. Gerberträger! 34 5.4. Fachwerke! 35 5.5. Dreigelenksrahmen und Dreigelenksbogen! 43 6. Anhang: Rechenregeln Tragwerkslehre 3! Seite 1 1.Einführung 1.1. Die Statik als Teilgebiet der Mechanik Als Teilgebiet der Physik beschreibt die Mechanik den Kräfte- und Bewegungszustand materieller Körper. Dies umschließt stets auch den Ruhezustand, das Gleichgewicht, als Sonderfall einer Bewegung. Je nach dem Aggregatzustand der untersuchten Stoffe wird eine Mechanik der festen, flüssigen und gasförmigen Körper unterschieden. Mechanik Mechanik fester Körper Kinematik Fluidmechanik 1.Aero- und Gasdynamik Dynamik Bewegungs- und Verformungszustände ohne Berücksichtigung einwirkender Kräfte Bewegungs- und Verformungszustände als Folge einwirkender Kräfte Kinetik zeithängige Kraft- und Verformungszustände. Beispiel: Karussell Assoziation: kinetische Energie Statik Ruhezustände als zeitunabhängige Sonderfälle von Bewegung. Beispiel: Dachstuhl In jedem dieser Gebiete beschäftigt sich die Kinematik mit der mathematischen Beschreibung von Bewegungs- und Verformungszuständen allein, also ohne Berücksichtigung der einwirkenden Kräfte, während die Dynamik die Bewegungsund Verformungszustände als Folge der einwirkenden Kräfte beschreibt. Das eigentliche Arbeitsgebiet der Statik bildet die Ermittlung des Kräfte- und Verformungszustands ruhender, d.h. sich im Gleichgewicht befindlicher Körper. Sie dient im Bauingenieurwesen der Ermittlung der Beanspruchungen und Verformungen von Tragwerken als Grundlage zu deren nachfolgender Bemessung. Tragwerkslehre 3! Einordnung der Statik innerhalb der Mechanik Statik als Sonderfall der Dynamik Kinematik Dynamik Zweck der Statik Seite 2 1.2. Sicherheit Ein Tragwerk ist dann korrekt bemessen, wenn sowohl die innere als auch die äußere Standsicherheit ausreichend gegeben ist. Begriffe Sicherheit und Versagen äußere Standsicherheit Statik ausreichende Sicherheit -> Normen Versagen durch Umstürzen, Gleiten, Aufschwimmen Liefert die Beanspruchung eines Tragwerks (innere Kräfte) Festigkeitslehre innere Standsicherheit Liefert die Verknüpfung zwischen Kräften und Verformungen/Spannungen Bemessung in Stahl, Stahlbeton, Holz Versagen durch Bruch ..... Beispiel für äußere und innere Standsicherheit: äußere und innere Standsicherheit Stützmauer stürzt als Ganzes um --> äußere Standsicherheit nicht gegeben Stützmauer bricht --> innere Standsicherheit nicht gegeben Beispiel für eine Bemessungsaufgabe: Träger auf zwei Stützen: Wahl des Profils/Querschnitts Holzbalken Tragwerkslehre 3! Stahlprofil Stahlbetonträger Seite 3 1.3. Modellbildung Bei einer statischen Berechnung wird ein Tragwerk idealisiert und in möglichst einfache Bestandteile (Tragelemente) zerlegt. Tragelemente: ! ! ! ! ! ! ! ! ! 3D-Struktur Platte, Schale, Scheibe 2D (d <<lx, d<<ly) Stabelemente 1D (b<<l, h<<l) gerade und gekrümmte Tragwerke: ! Begriffe Tragwerk Tragelemente Man unterscheidet : Stabwerke: ! das Tragwerk besteht nur aus Stabelementen ! Berechnung durch sog. Stabstatik Flächentragwerke: das Tragwerk besteht aus Flächentragelementen 3D-Tragwerke: das Tragwerk kann nur als 3D-Kontinuum berechnet werden (EDV-Einsatz) Tragwerkstypen Beispiele für Tragwerke: ! ! ! 1. für Stabwerke: Fachwerk, Rahmen, Trägerrost, Bogenträger 2. für Flächentragwerke: Kuppel, Gewölbe, Behälter, Deckenplatte 3. für 3D-Tragwerke: Schwergewichtsmauer, Maschinenfundament Reichen für die Berechnung eines Tragwerks die Gleichgewichtsbedingungen aus, so spricht man von einem statisch bestimmten Tragwerk. Ist dies nicht der Fall, so müssen zur Berechnung des Tragwerks Verformungen herangezogen werden. Man spricht dann von einem statisch unbestimmten Tragwerk. statisch bestimmte - statisch unbestimmte Tragwerke 1.4. Methoden der Statik In der Statik werden folgende Methoden eingesetzt: 1. Graphische Methoden (Krafteck, Seileck, Cremonaplan) 2. Rechnerische Methoden - für praktisch alle Problemtypen anwendbar 3. Experimentelle Methoden - wo keine Modellbildung möglich bzw. zur Überprüfung von Berechnungen und Theorien Tragwerkslehre 3! Seite 4 2. Kräfte 2.1. Definition Eine Kraft ist die Ursache einer Bewegungs- bzw. Formänderung von Körpern. Eine Kraft ist durch drei Bestimmungsstücke vollständig gegeben: Definition einer Kraft Bestimmungsstücke einer Kraft 1. Betrag (Größe) der Kraft [N, kN etc.] 2. Angriffspunkt 3. Wirkungsrichtung Die durch den Angriffspunkt und die Kraftrichtung bestimmte Gerade bezeichnet man als Wirkungslinie. Graphische Darstellung: Wirkungsrichtung Kraft F Y Betrag = 5 kN Angriffspunkt (5,2) Wirkungslinie X ! Kraftmaßstab: 1cm = 2 kN Zahlenmäßige Darstellung in Komponentenschreibweise: ! ! ! ! ! ! ! F = [Fx Fy]! ! bzw.!F = [Fx Fy Fz]! ! in E2 in E3 2.2. Arten von Kräften bzw. Lasten im Bauwesen • Unterscheidung nach Belastungskategorie: 1. ständige Lasten !! ! ! ! 2. Verkehrslasten bzw. Nutzlasten! ! 3. Gesamtlasten! ! ! ! ! g,G! Eigengewicht! ! p,P! Wohnbau 2kN/m2 q,Q • Unterscheidung nach der Lasteinwirkung: Einzellast F=20kN Linienlast Flächenlast p=6.0 kN/m p=6.0 kN/m2 Verteilte Lasten können gleichmäßig oder ungleichmäßig verteilt sein. Tragwerkslehre 3! Seite 5 2.2.1 Die Lastabtragung (oder wie man auf Einzel-, Linien und Flächenlasten kommt) Dachlasten: Eigengewicht, Schneelast, Windlast alle gleichförmig verteilte Flächenlasten Achsabstand Pfetten Achsabstand Fachwerke Lasteinzugsfläche der Pfetten Lasteinzugsfläche der Fachwerke Dachhaut quartär: Dachschalung Primär: Fachwerk Tertiär: Balken Sekundär: Pfette Die Hierarchie der Tragwerkselemente wird durch die Flussrichtung der Lasten bestimmt: im obigen Beispiel von der quartären Dachschalung über die tertiären Balken auf die sekundären Pfetten, welche wiederum auf den primären Fachwerken liegen. Zum Begriff der Lasteinzugsfläche: Die Lasteinzugsfläche eines Tragwerkselements ist jener Bereich eines Daches bzw. einer Decke, aus dem die Last in dieses Tragwerkselement fließt. Tragwerkslehre 3! Seite 6 2.3. Lehrsätze über Kräfte 2.3.1. Axiome Trägheitsaxiom Jeder Körper beharrt im Zustand der Ruhe (Gleichgewichtszustand) oder der gleichförmigen Bewegung, solange er nicht durch einwirkende Kräfte zu einer Änderung seines Zustands gezwungen wird (1. Newtonsches Gesetz). 2.3.2. Äquivalenzaxiom Zwei Kräfte heißen äquivalent (gleichwertig), wenn sie auf einen Körper die gleicheWirkung ausüben. Zwei Kräfte gleichen Betrages, gleicher Richtung und gleicher Wirkungslinie, jedoch unterschiedlichen Angriffspunkts, üben auf einen starren Körper offensichtlich die gleiche Wirkung aus. Somit sind sie äquivalent, d.h., Kräfte dürfen längs ihrer Wirkungslinie verschoben werden. Beispiel: Schieben oder Ziehen eines Wagens - äquivalente Kräfte 2.3.3. Verschiebungsaxiom Kräfte dürfen entlang ihrer Wirkungslinie beliebig verschoben werden (sie sind sog. linienflüchtige Vektoren). 2.3.4. Reaktionsaxiom Wird von einem Körper A eine Kraft FAB auf einen zweiten Körper B ausgeübt, so übt der Körper B die gleiche Kraft auf den Körper A aus. Beide Kräfte besitzen die gleiche Wirkungslinie, sind gleich groß, jedoch entgegengesetzt gerichtet: ! ! ! ! ! FAB = -FBA (actio = reactio; 3. Newtonsches Gesetz). Beispiel: Die Hand zieht am Seil mit 0.2 kN, also zieht auch das Seil an der Hand mit 0.2 kN. 2.3.5. Bildung der Resultierenden Parallelogrammaxiom Die Wirkung zweier Kräfte mit gleichem Angriffspunkt ist ihrer vektoriellen Summe äquivalent.(siehe Zentralsystem) F2 F1 2.3.6. R12 (Resultierende von F1 und F2) Resultierende Grundgesetz der Mechanik F=m*a (2. Newtonsches Gesetz) Tragwerkslehre 3! Seite 7 2.4. Das zentrale Kräftesystem Ein zentrales Kräftesystem (Zentralsystem) liegt vor, wenn alle vorhandenen Kräfte einen gemeinsamen Angriffspunkt besitzen (Sonderfall des allgemeinen Kräftesystems). Auf Grund des Verschiebungsaxioms ist diese Bedingung erfüllt, wenn sich die Wirkungslinien der Kräfte schneiden, da die Kräfte dann in den Schnittpunkt der Wirkungslinien hineinverschoben werden können. F1 F2 F3 2.4.1. Die Resultierende Das Parallelogrammaxiom läßt die schrittweise Bildung einer Resultierenden der angreifenden Kräfte zu. (Demonstrieren!). Die Resultierende R hat die gleiche Wirkung wie die angreifenden Kräfte F1, F2 und F3. R12 F1 R123 F2 Definition Gleichgewicht F3 Vereinfacht lässt sich die Resultierende durch vektorielle Addition der Einzelkräfte bilden. Dies ist aus dem obigen Beispiel ersichtlich. Tragwerkslehre 3! Seite 8 Beispiel: 0.80 h=6.0m γ=25 E=108 kN 2.0 2.0 Ermittle die Resultierende der Kräfte G und E. Zusatzfrage: Ist das System im Gleichgewicht? 2.4.2. Gleichgewicht Gleichgewicht liegt in einem Zentralsystem vor, wenn die Resultierende aller Kräfte gleich 0 ist. In Komponentenschreibweise lautet die Gleichgewichtsbedingung daher: ! ! ! ! ! ! Begriff Drehmoment ∑ Fx = 0 ∑ Fy = 0 Beispiel: Dübelaufhängung für 4 Seile. Welche Kraft muss der Dübel aufnehmen, damit das System im Gleichgewicht ist? Graphisch und numerisch durchführen! R Tragwerkslehre 3! Seite 9 2.5. Das allgemeine ebene Kräftesystem Ein allgemeines ebenes Kräftesystem liegt vor, wenn sich die Kräfte nicht einem Punkt oder gar nicht schneiden. Es tritt in diesem allgemeinen Fall eine Drehwirkung auf, Drehmoment genannt. Begriff Kräftepaar F1 F2 R123 = 0 M≠0 F3 2.5.1. Grundbegriffe Satz: Unter dem Begriff Moment bzw. Drehmoment versteht man die Drehwirkung einer Kraft um einen bestimmten Punkt. Der Betrag eines Momentes ist das Produkt von Kraftgröße mal Normalabstand zum Drehpunkt. ! M=Fxa M a F Definition Gleichgewicht P Ein Drehmoment kann auch als Vektor dargestellt werden, der normal zur Zeichenebene wirkt. (Momentenvektor). Vorzeichenkonvention: Rechtsschraubenregel a F P P == M Tragwerkslehre 3! F Seite 10 Das Kräftepaar F a d1 F P1 P2 P3 M1 = F(d1+a) - F d1 = F a M2 = F(d2+a) - F d2 = F a M≡Fxa Definition: Zwei Kräfte F im Abstand a, parallel, jedoch gegensinnig gerichtet. Eigenschaft: Das Moment eines Kräftepaares ist auf jeden Punkt der Ebene gleich groß. 2.5.2. Gleichgewicht im allgemeinen ebenen Kräftesystem Gleichgewicht liegt in einem allgemeinen ebenen Kräftesystem vor, wenn die Resultierende aller Kräfte 0 ist und auch das Drehmoment M gleich 0 ist. In Komponentenschreibweise lautet die Gleichgewichtsbedingung daher: ! ! ! ! ! ! 2.5.3. ! ! ! ∑ Fx = 0! ! ∑ Fy = 0 ∑ M = 0! ! keine Translation keine Rotation --> Ruhezustand Die Resultierende im allgemeinen ebenen Kräftesystem Die Resultierende muss definitionsgemäß den Einzelkräften äquivalent sein, und zwar sowohl was die Kraftwirkung an sich anbelangt als auch was die Drehwirkung anbelangt. Der Betrag und die Richtung der Resultierenden wird wie im Zentralsystem durch vektorielle Addition der Einzelkräfte ermittelt. Die Ermittlung der Lage der Resultierenden erfolgt graphisch über die Bildung von Teilresultierenden oder die sogenannte Seileckskonstruktion und rechnerisch über den Momentensatz. Tragwerkslehre 3! Seite 11 2.5.3.1. Graphische Lösung Graphische Lösung über Teilresultierende M 1:50 KM: 1cm = 20 kN 0.8 4.5 G1 E=95 kN 1.7 1.5 G2 2.0 ϕ=10° R1 E G1=140.625 3.0 R E G2 = 112.5 Anmerkung: Nur dann anwendbar, wenn sich die Kräfte auf der Zeichenebene schneiden! Tragwerkslehre 3! Seite 12 Die Seileckskonstruktion Anmerkung: Auch anwendbar, wenn sich die Kräfte nicht auf der Zeichenebene oder überhaupt nicht schneiden. M 1:50 KM: 1cm = 20 kN 0.8 4.5 G1 E=95 kN 1.7 1.5 G2 ϕ=10° G1=140.625 2.0 1 3.0 R 2 E 3 Pol G2 = 112.5 Tragwerkslehre 3! 4 Seite 13 2.5.3.2. Rechnerische Lösung Momentensatz: Die Summe der Drehmomente der Einzelkräfte um einen Drehpunkt D ist gleich dem Drehmoment der Resultierenden um denselben Drehpunkt D. M = ∑ Fi × ai = R × aR ⇒ aR = ∑ Fi × ai R € F3 F1 F2 aR D R F2 = 4.0 kN F1 = 2.0 kN 5.0 Lage von R = ? Beispiel: Beispiel: Berechne Größe und Lage der Resultierenden für obige Stützmauer mit Hilfe des Momentensatzes. Hinweis: Abstand der Wirkungslinie von G1 zur Hinterseite der Stützmauer a1 = 0.652 m. Tragwerkslehre 3! Seite 14 Tabellarische Bestimmung der Größe und Lage der Resultierenden mit Hilfe des Momentensatzes Vorzeichenvereinbarungen: Y F +F y x A M D = -Fx *(y-y D) + Fy *(x-x D) +ϕ + +F x y xD D yD X Beispiel: Y R F1 = 4 kN F2 = 2.828 F3 = 5 F4 = 2 D = (1,0) X x3 = 9.0 x2 = 7.0 x1 = 3.0 x4 = 14.0 F phi x y Fx Fy -Fx*(y-yD) Fy*(x-xD) [kN] Grad [m] [m] kN kN kNm kNm 4,000 -90,000 3,000 0,000 0,000 -4,000 0,000 -8,000 2,828 -45,000 7,000 0,000 2,000 -2,000 0,000 -12,000 5,000 240,000 9,000 0,000 -2,500 -4,330 0,000 -34,641 2,000 90,000 14,000 0,000 0,000 2,000 0,000 26,000 4,438 0,000 -0,500 -8,330 0,000 -28,641 Rx = -0,500 kN Ry = -8,330 kN R= 8,345 kN MD = -28,641 kNm MD/Ry = 3,438 m xR = 4,438 m Tragwerkslehre 3! xD yD 1,000 0,000 Seite 15 Beispiel 2: Y 0.8 4.5 G1 = 90 G3 = 50.625 E=95 kN 1.7 1.5 D ϕ=10° 2.0 G3 = 112.5 3.0 X D = (0,0): F phi x y Fx Fy -Fx*(y-yD) Fy*(x-xD) xD yD [kN] Grad [m] [m] kN kN kNm kNm m m 90,000 -90,000 2,600 3,750 0,000 -90,000 0,000 -234,000 0,000 0,000 112,500 -90,000 1,500 0,750 0,000 -112,500 0,000 -168,750 50,625 -90,000 1,900 3,000 0,000 -50,625 0,000 -96,188 95,000 -170,000 3,000 2,000 -93,557 -16,497 187,113 -49,490 1,340 0,000 -93,557 -269,622 187,113 -548,427 Rx = -93,557 kN Ry = -269,622 kN R= 285,392 kN MD = -361,314 kNm MD/Ry = 1,340 m xR = 1,340 m F phi x y Fx Fy -Fx*(y-yD) Fy*(x-xD) [kN] Grad [m] [m] kN kN kNm kNm 90,000 -90,000 2,600 3,750 0,000 -90,000 0,000 36,000 112,500 -90,000 1,500 0,750 0,000 -112,500 0,000 168,750 50,625 -90,000 1,900 3,000 0,000 -50,625 0,000 55,688 95,000 -170,000 3,000 2,000 -93,557 -16,497 187,113 0,000 1,340 0,000 -93,557 -269,622 187,113 260,438 1 D = (3,0): Rx = -93,557 kN Ry = -269,622 kN R= 285,392 kN MD = 447,551 kNm MD/Ry = -1,660 m xR = 1,340 m Tragwerkslehre 3! xD yD 3,000 0,000 Seite 16 2.5.4 Besondere Eigenschaften von Kräften und Kräftepaaren Satz: Kräftepaare dürfen in der Ebene beliebig verschoben und gedreht werden. F F = F F F Y F = F x1 F x2 X Satz: Kräftepaare sind äquivalent, wenn das von ihnen ausgeübte Drehmoment gleich groß ist. F1 = F1 F2 a1 F2 a2 <=> F1 a1 = F2 a2 Satz: Die Resultierende einer Kraft F und eines Kräftepaars ist eine in gleicher Richtung wirkende Kraft im Abstand a. F F a Tragwerkslehre 3! + x F = F F F = F a x-a Seite 17 Satz: Eine Kraft F läßt sich in der Ebene um den Abstand a quer zu seiner Wirkungslinie verschieben, wenn ein Kräftepaar (F,a) hinzugezählt wird. Dies ist eine Umkehrung des letzten Satzes. M= F*a F x Tragwerkslehre 3! = F F x a F = F x+a Seite 18 3. Schwerpunktsberechnungen 3.1. Schwerpunkt von Linienzügen Der Schwerpunkt einer einzelnen Linie liegt in Linienmitte. Y y2 P2 (y1+y2)/2 S y1 P1 x1 (x1+x2)/2 x2 X Der Schwerpunkt eines Linienzuges kann entweder graphisch mittels Seileck oder rechnerisch mit Hilfe des Momentensatzes ermittelt werden. In der Praxis werden sog. „dünnwandige Querschnitte“ als Linienzüge idealisiert. (C,U,Z Profile etc.) Das Gewicht Gi einer einzelnen Linie des Linienzugs ist dabei Gi = li*di. Wenn d bei allen Linien gleich ist, fällt es aus der Berechnung heraus. Y 3 2 2 1 1 3 S 6 5 4 4 5 X umgeformter Momentensatz: xS = ∑Gi*xi/∑G yS = ∑Gi*yi/∑G Tragwerkslehre 3! Seite 19 ! Tabellarische Berechnung Pkt. xi yi Linie xsi ysi Gi (=Li) Gi*xsi Gi*ysi 1 5,00 6,20 1 5,00 7,20 2,000 10,000 14,400 2 5,00 8,20 2 3,40 8,20 3,200 10,880 26,240 3 1,80 8,20 3 1,80 4,85 6,700 12,060 32,495 4 1,80 1,50 4 3,95 1,50 4,300 16,985 6,450 5 6,10 1,50 5 6,80 2,25 2,052 13,952 4,617 6 7,50 3,00 18,252 63,877 84,202 xs = 3,500 ys = 4,613 Übung 1: Ermittlung des Schwerpunkts des obigen Beispiels mittels Seileck! Übung 2: Wie Ü1, jedoch sei Linie 4 doppelt so dick wie die übrigen Linien. 3.2. Schwerpunkt von Flächen Wird völlig analog zur Schwerpunktsermittlung bei Linienzügen durchgeführt. Die gesamte Fläche wird in geometrisch möglichst einfache Teilflächen (Rechtecke und Dreiecke, ev. Trapeze) unterteilt. Dann wird wiederum der Momentensatz oder die Seileckskonstruktion angewandt. 2.2 7.5 Symmetrie A1 1.5 Y A2 5.0 A3 A4 2.3 X (0,0) 4.6 Tragwerkslehre 3! Seite 20 Tabellarische Berechnung Fläche xsi ysi Gi (=Ai) Gi*xsi Gi*ysi 1 5,95 8,05 11,25 66,94 90,56 2 3,40 4,80 12 40,80 57,60 3 1,47 4,47 7,15 10,49 31,94 4 2,30 1,15 10,58 24,33 12,17 40,980 142,558 192,266 xs = 3,479 ys = 4,692 3.3. Schwerpunkt symmetrischer Flächen und Linienzüge Symmetrieachsen sind zugleich Schwerachsen sind, was sich natürlich sehr vorteilhaft ausnützen läßt: 1. Bei einfachsymmetrischen Flächen ist eine der beiden Schwerachsen bekannt und nur eine solche muss ermittelt werden. 2. Bei zwei- oder mehrfachsymmetrischen Flächen ist der Schwerpunkt von vornherein bekannt, er liegt im Schnittpunkt zweier Symmetrieachsen. 3. Bei punktsymmetrischen Flächen ist der Schwerpunkt gleich dem Symmetrieursprung. Aktions- und Reaktionskräfte Tragwerkslehre 3! Seite 21 4. Ebene Stabwerke Bei der Berechnung von Stabwerken wie auch von Tragwerken im allgemeinen ist nachzuweisen, dass 1. die äußere Standsicherheit gegeben ist 2. die innere Standsicherheit gegeben ist. 4.1. Äußere Standsicherheit - Ermittlung der Auflagerreaktionen Die äußere Standsicherheit eines Tragwerks ist gegeben, wenn kein Versagen durch Umkippen, Gleiten etc. auftritt, oder präziser: wenn das Tragwerk unter der Einwirkung der äußeren Kräfte keine Bewegung (Translation, Rotation) erleidet. Voraussetzung für die äußere Standsicherheit ist daher der Ruhezustand des Tragwerks. Ein Tragwerk ist dann in Ruhe, wenn alle äußeren Kräfte miteinander im Gleichgewicht sind. In der Ebene ist das der Fall, wenn gilt ! ! ! ! ! ∑ Fx = 0! ! keine Translation ! ! ! ∑ Fy = 0 !! ! ! } Ruhezustand ! ! ! ∑ M = 0! ! keine Rotation ! siehe 2.5.2 In E3 müssen statt drei gleich sechs Gleichgewichtsbedingungen erfüllt sein: ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ∑ Fx = 0 ∑ Fy = 0 ∑ Fz = 0! ! ∑ Mx = 0 ∑ My = 0! ! ∑ Mz = 0 !keine Translation keine Rotation Zu den äußeren Kräften gehören: ! ! 1. die Lasten (Eigenlasten, Verkehrslasten) oder Aktionskräfte 2. die Auflagerkräfte = Reaktionkräfte F (äußere Kräfte) Tragwerk A1 Tragwerkslehre 3! A2 (Auflagerreaktionen Seite 22 Mit anderen Worten: Gleichgewicht liegt vor, wenn die Aktionskräfte (Lasten) sich mit den Auflagerreaktionskräften aufheben. Die Auflager müssen daher so ausgelegt werden, dass ein Tragwerk keine Bewegungsmöglichkeiten mehr hat. Der Nachweis der äußeren Standsicherheit bedeutet, dass die vorhandenen Auflagerreaktionen den maximal möglichen gegenüber gestellt werden. Liegt ein genügend großer Sicherheitsabstand vor, so ist die äußere Standsicherheit gegeben. Die erste Aufgabe innerhalb der statischen Berechnung eines Tragwerks ist daher die Ermittlung der Auflagerreaktionen. Diese kann graphisch und rechnerisch erfolgen. 4.1.1. Arten von Auflagern a) Einwertige Lager: Können nur Kräfte in einer Richtung aufnehmen. ! ! Symbole: ! ! ! ! Beispiele: Rollenlager, Gleitlager, Pendelstab b) Zweiwertige Lager: Können Kräfte in beiden Richtungen X und Y, jedoch keine Drehmomente aufnehmen. Sog. feste Lager. ! Symbol: ! ! ! ! ! ! c) Dreiwertige Lager: Können Kräfte in beiden Richtungen X und Y und auch Drehmomente aufnehmen. Sog. Einspannung. ! Symbol: ! ! ! Tragwerkslehre 3! Seite 23 4.1.2. Rechnerische Ermittlung der Auflagerreaktionen Für die Ermittlung der Auflagerreaktionen werden die drei Gleichgewichtsgleichungen (siehe oben) herangezogen. Beispiel 1: F1 x1 A F1 = 20 kN F2 = 30 kN L=6m x1 = 2 m F2 x2 L B ∑Fx = 0:! Ax + Bx + F1x + F2x = 0! => Ax = Bx = 0 ∑Fy = 0:! Ay + By + F1y + F2y = 0! => Ay + By = - F1y - F2y ∑MA= 0:! By*L + F1y*x1 + F2y*x2 = 0! => By = (-F1y*x1 - F2y*x2 )/L Achtung: Kraftkomponenten mit dem Vorzeichen einsetzen! Beispiel 2: F2 F1 A x1 45˚ L1 B x2 L2 F1 = 20 kN F2 = 30 kN L1 = 6.0 m L2 = 2.5 m x1 = 2.0 m Beispiel 3: F1 A x1 L B F1 = 20 kN L=6m x1 = 2 m 45˚ Beispiel 4: F2 = 35 kN F1 = 35 kN (2.0/0) Tragwerkslehre 3! (6.0/2.0) (10.0/2.0) (4.0/0) Seite 24 4.1.3. Graphische Ermittlung der Auflagerreaktionen Gleichgewicht liegt vor, wenn die Aktionskräfte (Lasten) sich mit den Auflagerreaktionskräften aufheben. Siehe oben. Dies bedeutet, dass die Resultierende der Lasten gleich groß sein und die gleiche Wirkungslinie haben, jedoch entgegengerichtet sein muss. Beispiel 1: F1 = 20 kN F2 = 30 kN L=6m x1 = 2 m F1 A x1 F2 L x2 B A 1 S 2 B 3 Beispiel 2: F1 = 20 kN F2 = 30 kN L=6m x1 = 2 m F1 A x1 F2 L x2 B S A 1 2 B 3 Tragwerkslehre 3! Seite 25 Beispiel 3: Tragwerkslehre 3! Seite 26 4.2. Innere Standsicherheit - Ermittlung der inneren Kräfte (Schnittgrößen) Die innere Standsicherheit eines Tragwerks ist gegeben, wenn kein Versagen durch Fließen oder Bruch auftreten kann, mit anderen Worten, wenn die im Inneren eines Tragwerks wirkenden Kräfte einen genügend großen Sicherheitsabstand zu den gerade noch ertragbaren Grenzkräften aufweisen. Die inneren Kräfte werden auch Schnittkräfte bzw. Schnittgrößen genannt. 4.2.1. Arten von Schnittgrößen Im Fall ebener Systeme gibt es drei Arten von Schnittgrößen: 1. Normalkräfte So benannt, weil sie normal zur Schnittfläche wirken. F Schnittfläche F N=F Symbol: N Vorzeichendefinition: Zug positiv 2. Querkräfte So benannt, weil sie quer zur Stabachse wirken. Schnittfläche F V=F Symbol: V (Q) Vorzeichendefinition: rechtes Schnittufer nach unten positiv Tragwerkslehre 3! Seite 27 3. Biegemomente Bewirken eine Verbiegung der Stabachse. Schnittfläche F a M = Fxa Sätze zur Schnittgrrößenermittlung Symbol: M Vorzeichendefinition: Bezugsfaser gezogen - positiv die Bezugsfaser wird i.a. an der Stabunterseite angenommen. Alternative Definition: Momentenvektor am rechten Schnittufer in die positive z-Richtung wirkend = positiv 4.2.2. Vorzeichen der Schnittgrößen am herausgeschnittenen Element Achtung: Diese Vorzeichendefinition hat nichts mit der Vorzeichendefinition für die Auflagerkräfte zu tun! Die inneren Kräfte sind auf die beliebig liegende Stabachse (sog. lokales Koordinatensystem) bezogen, die Auflagerkräfte auf ein globales Koordinatensystem. Tragwerkslehre 3! Seite 28 4.2.3. Rechnerische Ermittlung der Schnittgrößen Satz: Wenn das gesamte System im Gleichgewicht ist, so befindet sich auch jedes beliebige Teilsystem des Tragwerks im Gleichgewicht. Satz: An der Schnittstelle werden die inneren Kräfte zu äußeren Kräften. Aufgabe der statischen Berechnung ist es, an jeder Stelle des Tragwerks die inneren Kräfte (Schnittgrößen) zu ermitteln. Diese werden dann in einem Diagramm aufgetragen. Auf der Grundlage der beiden obigen Sätze wird an einer Stelle x ein Schnitt geführt, wodurch zwei Teilsysteme entstehen, die für sich im Gleichgewicht sein müssen. Man betrachtet nun eines dieser Teilsysteme und errechnet sich jene äußeren Kräfte an der Schnittstelle, die für das Gleichgewicht dieses Teilsystems erforderlich sind. Beispiel 1: F V=F (-) H [N] [V] N=H -l- +x V(-) x M=F*x N Teilsystem muss im Gleichgewicht sein! d.h. ∑Fx = 0 ∑Fz = 0 ∑M = 0 (+) (-) M=F*l [M] (-) Beispiel 2: Beispiel 3: Tragwerkslehre 3! Seite 29 4.2.4. Eigenschaften der Querkraft- und Momentenbilder 1. Belastung durch Einzellasten: • Querkraftbild: Zwischen den Kräften ist die Querkraft konstant, am Angriffspunkt der Kräfte weist die Querkraft einen Sprung in der Größe der Kraft auf. • Momentenbild: Zwischen den Kräften verläuft die Momentenlinie linear, unter den Kräften weist die Momentenlinie einen Knick auf. 2. Belastung durch Gleichlasten: • Querkraftbild: Unter einer Gleichlast verläuft die Querkraftlinie linear. • Momentenbild: Unter einer Gleichlast hat die Momentenlinie die Form einer quadratischen Parabel. Weitere wichtige Sätze: 1. Wo die Querkraft Null ist, nimmt das Biegemoment ein Extremum an. 2. Das Moment an einer beliebigen Stelle x entspricht dem Flächeninhalt des Querkraftbildes bis zu dieser Stelle. 3. Die Schnittgrößen aus zwei oder mehreren einzelnen Lastzuständen dürfen addiert werden, um die resultierenden Schnittgrößen für die Gesamtlast zu erhalten. (sog. Überlagerungsgesetz/Superpositionsgesetz) Beispiel zum Überlagerungsgesetz: F1 (-) [M1] + + F (+) = F1 = F (-) (+) Tragwerkslehre 3! [M2] [M]=[M1]+[M2] Seite 30 Mit Hilfe des Überlagerungssatzes zu lösendes Beispiel: q Tragwerkslehre 3! F Seite 31 5. Besondere Tragwerke 5.1. Schräge Träger Beispiel 1: B g=2.0kN/m 3.0 A 4.0 Beispiel 2: B w=2.0kN/m 3 A 4.0 Tragwerkslehre 3! Seite 32 5.2. Geknickte Träger Beispiel 1: Beispiel 2: q Begriff statisch unbestimmt Beispiel 3: M Tragwerkslehre 3! Seite 33 5.3. Gerberträger In der Praxis sind häufig mehrere Felder mit einem Träger zu überspannen. Man spricht dann von einem sog. Mehrfeldträger. Zur Ausbildung eines Mehrfeldträgers gibt es grundsätzlich folgende Möglichkeiten: 1. Kette von Einzelträgern statisch bestimmt 2. Gelenk- oder Gerberträger statisch bestimmt ideale Fachwerke Voraussetzungen 3. Durchlaufträger statisch unbestimmt Um einen statisch unbestimmten Durchlaufträger in ein statisch bestimmtes System umzuwandeln, sind soviele Gelenke anzuordnen, wie es Innenstützen gibt. In einem Gelenk gilt: M=0 (sog. Momentengelenk). Dadurch werden zusätzliche Gleichungen erhalten, die das system mit Hilfe der Gleichgewichtsgleichungen wieder lösbar machen. Werden die Gelenke über den Auflagern angeordnet, so spricht man von einer Trägerkette. Ordnet man die Gelenke hingegen in den Feldern an, so bezeichnet man das Tragwerk als Gerberträger. Bei einem Gerberträger müssen die Gelenke sinnvoll angeordnet werden, d.h.: 1. In den Endfeldern darf jeweils nur ein Gelenk sein. 2. Mittelfelder dürfen zwei Gelenke haben. In diesem Fall dürfen die Nachbarfelder jedoch kein Gelenk besitzen. 3. Nur ein Auflager ist fest. Alle anderen Lager sind Gleitlager. Damit ist die eindeutige Ableitung der Horizontalkräfte gewährleistet. Ungünstige Anordnung: Koppelträger Tragwerkslehre 3! Seite 34 5.4. Fachwerke 5.4.1. Grundlagen Abzählkriterium ebene räumliche Fachwerke Fachwerke bestehen aus zug- und druckfesten Stäben, die in Knotenpunkten miteinander verbunden sind. Liegen Stabachsen, Knotenpunkte und Lasten in einer Ebene, so sprechen wir von ebenen Fachwerken, im anderen Fall von räumlichen Fachwerken. Zur Berechnung der Schnitt- und Auflagergrößen werden folgende, durch Karl Culmann 1851 eingeführte Voraussetzungen getroffen: ! ! ! ! 1. alle Stabachsen seien gerade; 2. alle Stäbe seien in den Knotenpunkten zentrisch und 3. durch reibungsfreie Gelenke miteinander verbunden; 4. es treten nur Knotenlasten auf, die Stäbe selbst seien unbelastet. Fachwerke, die diese Voraussetzungen erfüllen, heißen ideale Fachwerke. Als Folge dieser Idealisierungen bleiben die Knotenpunkte und somit die Stäbe biegemomentenfrei. Als einzige Schnittgröße treten somit Normalkräfte (sog. Stabkräfte ) auf. Wirkliche Fachwerke entsprechen den getroffenen Idealisierungen jedoch nur unvollständig. Siehe Bild unten. Tragwerkslehre 3! Seite 35 Für die Unterscheidung von statisch bestimmten und statisch unbestimmten Fachwerken gibt es das sog. Abzählkriterium: ! n = a + p - 2k! ! (ebene Fachwerke) n = a + p - 3k! ! (räumliche Fachwerke) bzw. ! Die einzelnen Parameter bedeuten dabei: ! ! ! a ... Anzahl der Auflagerreaktionen p ... Anzahl der Stäbe k ... Anzahl der Knotenpunkte Es gilt: ! n > 0 ... statisch unbestimmtes Fachwerk ! n = 0 ... statisch bestimmtes Fachwerk ! n < 0 ... statisch unterbestimmtes Fachwerk (= kinematisch verschieblich) 5.4.2. Fachwerksarten Man unterscheidet grundsätzlich ! • einfache ! • komplexe oder nicht-einfache Fachwerke (Fachwerkscheiben). Siehe Bild unten. Definition für einfache Fachwerkscheiben: Eine einfache Fachwerkscheibe entsteht aus einem Stabdreieck, wenn jeder neue Knoten durch 2 neue, nicht auf einer Geraden liegende Stäbe angeschlossen wird. Einfache Fachwerkscheiben sind statisch bestimmt. Tragwerkslehre 3! Seite 36 Ausfachungsarten von Fachwerken: Tragwerkslehre 3! Seite 37 Konstruktionsformen von Fachwerken: Tragwerkslehre 3! Seite 38 5.4.3. Rechnerische Ermittlung der Stabkräfte statisch bestimmter Fachwerke Bei der rechnerischen Bestimmung der Stabkräfte stehen zwei Verfahren zur Verfügung: ! 1. Ansatz der Knotengleichgewichtsbedingungen für jeden Knoten Hierbei wird ein Rundschnitt um jeden einzelnen Knoten geführt. Jeder Knoten stellt ein Zentralsystem dar. Die Stabkräfte können somit unter Ansatz der Gleichgewichtsbedingungen ∑Fx = 0 und ∑Fy=0 errechnet. werden. Die Methode ist stets anwendbar, hat aber den Nachteil, dass alle vor einem bestimmten Stab liegenden Stäbe gleich mitberechnet werden müssen. 2. Ansatz des Gleichgewichts an einem beliebigen Teilsystem (Ritter) Das System wird so aufgetrennt, dass drei Stäbe geschnitten werden, die sich nicht alle in einem Punkt treffen. Durch Ansatz der Gleichgewichtsbedingungen lassen sich die Kräfte der geschnittenen Stäbe errechnen. Die Methode ist nur in Kombination mit dem Ringschnitt anwendbar, hat aber den Vorteil, gezielt Stabkräfte zu liefern. ! Beispiel für die Stabkraftsermittlung mittels Knotengleichgewichtsbedingungen: A F B F F Beispiel für die Ermittlung der Stabkräfte am Teilsystem: F/2 A Tragwerkslehre 3! F F F F F F/2 B Seite 39 5.4.4. Graphische Ermittlung der Stabkräfte statisch bestimmter Fachwerke (Cremonaplan) Beim Cremonaplan wird der Reihe nach für jeden Knoten ein Krafteck gezeichnet. Jede Stabkraft scheint dabei in zwei Kraftecken auf, da er an zwei Knoten angeschlossen ist. Die einzelnen Kraftecke für die Knoten des Fachwerks können durch geschickte Vorgangsweise so ineinander geschoben werden, dass ein Kraftplan entsteht, in dem jeder Stab nur einmal vorkommt. Das Verfahren ist das graphische Äquivalent des Rundschnittverfahrens. Vorgangsweise: 1. Man beginnt wie beim Rundschnittverfahren bei einem Knoten mit max. 2 unbekannten Stabkräften. Die unbekannten Stabkräfte werden unter Zuhilfenahme des Parallelogrammaxioms ermittelt. 2. Bei jedem Knoten sind die Kräfte (Stabkräfte und äußere Kräfte) in einem bestimmten Umfahrungssinn aufzutragen. Dieser Umfahrungssinn ist über das ganze Fachwerk beizubehalten. Man beginnt mit der letzten bekannten Kraft gegen den Umfahrungssinn. 3. Die Wirkungsrichtung bzw. das Vorzeichen der Stabkräfte kann direkt aus dem Cremonaplan entnommen werden. Tragwerkslehre 3! Seite 40 F=8kN F=8kN 7 6 F=8kN 11 5 9 1 10 12 2 3 8 13 4 12kN 12kN Cremonaplan KM: 1cm = 2.5 kN F 8 B 10 F 7 6 1 3 11 12 A 5 F Beispiel 2 für Cremonaplan: 1. Beispiel für den Rundschnitt (siehe oben) Tragwerkslehre 3! Seite 41 5.4.5. Besonderheiten parallelgurtiger Fachwerke Parallelgurtige Fachwerke können mittels eines Ersatzträgers besonders leicht berechnet werden. Beispiel: F/2 F F F F F A F/2 B [V] [M] Diagonalen: ! D = V/sinϕ (+ fallende/ - für steigende Diagonalen) Pfosten:! ! P=V Gurte:! ! N = M/h Tragwerkslehre 3! Seite 42 5.5. Dreigelenksrahmen und Dreigelenksbogen Beispiele: Begriffe: Stützlinie, Kern Dreigelenksbogen Dreigelenksrahmen Sparrendach Dreigelenksbogen und Dreigelenksrahmen besitzen zwei feste Auflager und somit vier unbekannte Auflagerreaktionen. Diesen vier Unbekannten stehen drei Gleichgewichtsgleichungen (∑Fx=0,∑Fy=0,∑M=0) sowie eine zusätzliche Gleichung für das Gelenk (∑M=0) gegenüber. Damit sind diese Systeme statisch bestimmt. Beispiel: F Tragwerkslehre 3! Seite 43 Beispiel Dreigelenksbogen: 10 10 10 10 x=4 x=3 Stützlinie x=2 Ax Bx x=1 x=y=3.5355 Sy F1 By Sx R=5 F2 R1 Ax ϕ α=45° R2 Ay Ay R3 F3 x=0 R4 F4 By R5 Bx Gl1: ∑Fx=0: Ax + Bx = 0 Gl2: ∑Fy=0: Ay+By-40 = 0 Gl3: ∑Mb=0: Ay*8.5355 - Ax*3.5355 - 10*(4.535+5.535+6.535+7.535) = 0 Gl4: ∑Mg=0: Ay*5-Ax*5-10*(4+3+2+1) = 0 Ax = Ay-2*(4+3+2+1) = Ay-20 -> Gl3: Ay*8.535-3.535*(Ay-20) - 241.421 = 0 Ay*(8.535-3.535) + 20*3.535 - 241.421 = 0 Ay = 1/5*(241.421-20*3.535) = 34.142 kN Ax = Ay - 20 = 14.142 kN Bx = -Ax = -14.142 kN By = 40 - Ay = 40 - 34.142 = 5.858 kN! ! Probe: ∑Mg=0 mit Bx und By! Berechnung der Normalkraft und der Querkraft: Q(ϕ) = Sy sin(ϕ) − Sx cos(ϕ) N(ϕ) = −Sy cos(ϕ) − Sx sin(ϕ) Tragwerkslehre 3! Seite 44 Tabellarische Schnittgrößenbestimmung: S x Sy phi Q(phi) N(phi) 14,142 34,142 0,000 -14,142 -34,142 14,142 34,142 10,000 -7,998 -36,079 14,142 34,142 20,000 -1,612 -36,920 14,142 34,142 30,000 4,824 -36,639 14,142 34,142 36,800 9,128 -35,810 14,142 24,142 36,800 3,138 -27,803 14,142 24,142 53,130 10,828 -25,799 14,142 14,142 53,130 2,828 -19,799 14,142 14,142 66,420 7,304 -18,618 14,142 4,142 66,420 -1,861 -14,618 14,142 4,142 78,460 1,229 -14,685 14,142 -5,858 78,460 -8,569 -12,684 14,142 -5,858 90,000 -5,858 -14,142 14,142 -5,858 105,000 -1,998 -15,176 14,142 -5,858 120,000 1,998 -15,176 14,142 -5,858 135,000 5,858 -14,142 Tragwerkslehre 3! M(phi) Seite 45 Anhang: Rechenregeln Angeschrieben werden Rechenergebnisse auf min. 3 und max. 4 signifikante Stellen. Beispiele: ! Genaues Ergebnis 34567,8 -> angeschrieben wird 34600 ! Genauer Wert: 0,012345 -> angeschrieben wird 0,0123 Wichtig: Signifikante Stellen nicht verwechseln mit Dezimalstellen! Ob man 3 oder 4 signifikante Stellen wählt, ist Geschmacksache, bereits bei drei Stellen ist eine Genauigkeit von 1 Promille gegeben, was angesichts der Ungenauigkeit der Eingangsgrößen mehr als genug ist. Gerechnet wird stets mit voller Genauigkeit. D.h., dass Zwischenergebnisse im Taschenrechner gespeichert werden müssen, damit die Genauigkeit nicht verlorengeht. Für den unwahrscheinlichen Fall, dass man Zwischenergebnisse aufschreibt und dann wieder eintippen muss, empfehle ich die Mitnahme von min. 5 signifikanten Stellen, damit letztlich eine Genauigkeit von drei bis vier signifikanten Stellen im Ergebnis erhalten bleibt. Tragwerkslehre 3! Seite 46