Skalarprodukt mit einem Einheitsvektor

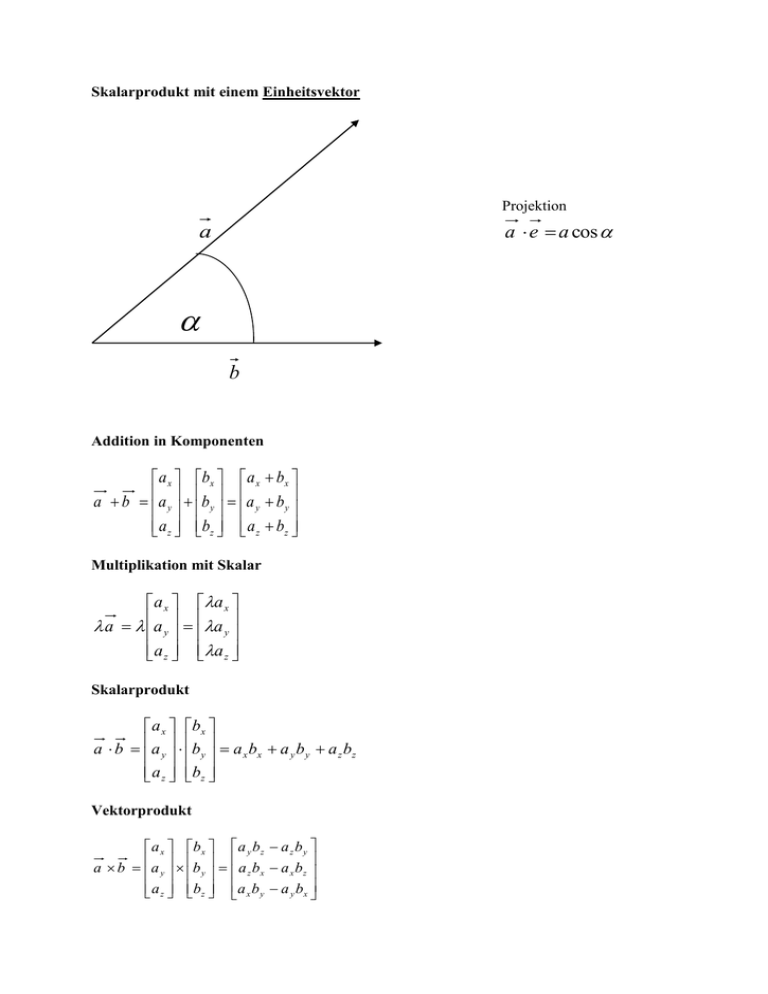
Skalarprodukt mit einem Einheitsvektor
Projektion
a  e  a cos 
a

b
Addition in Komponenten
 a x  b x   a x  b x 
a  b  a y   b y   a y  b y 
 a z  bz   a z  bz 
Multiplikation mit Skalar
 a x   a x 
 a   a y   a y 
 a z  a z 
Skalarprodukt
 a x  b x 
a  b  a y   b y   a x bx  a y b y  a z bz
 a z  bz 
Vektorprodukt
 a x  b x   a y b z  a z b y 


a  b  a y   b y    a z bx  a x bz 
 a z  bz  a x b y  a y bx 
1.3 Ebene Kräftesysteme
Kraft :
Betrag 
 Vektor
Richtung 





 gebundener Vektor




Wirkungsli nie
Statische Äquivalenz
Ebenes Kräftesystem
Ziel: Zusammenfassen zu einer
statisch äquivalenten Kraft
Reduktion der Aufgabe:
2 Kräfte zu einer statisch
äquivalenten Kraft
zusammenfassen.
Fall 1: Kräfte haben denselben Angriffspunkt
F1  F2
F2
F1
Fall 2: Kräfte mit verschiedenen Angriffspunkten
F2
F1  F2
F2
F1
F1
Fall 3: Parallele Kräfte
F2  F0
F0
F2
F1  F2
F1
 F0
F1  F0
Fall 4: Ausnahmefall „Kräftepaar“ oder „Kräftdipol“
F0  F1
Ein ebenes Kräftesystem ist
statisch äquivalent
- entweder zu einer Einzelkraft
F0
F1
 F1
- oder zu einem Kräftdipol
 F0
 ( F0  F1 )
1.4 Kräftedipol und statisches Moment
Transformation eines Kräftedipols
a' F '

a F
a
a’
F
a' F '  aF
statisches Moment
F’
1.5 Räumliche Kräftesysteme
Räumliches Kräftesystem i.a. statisch
äquivalent zu
- einer Einzelkraft
- und einem Kräftedipol, repräsentiert
durch seinen Momentenvektor
„Verpflanzung“ einer Kraft in einen anderen Angriffspunkt
F in P F in P, F in O,
 F in O
 F in O, F in P,F in O
F
P
r
F
Kräftedipol repräsentiert
durch Momentenvektor
M  r F
O
F
Räumliches Kräftesystem
FK
FK
Kräftesystem, bestehend aus n
Kräften FK mit Angriffspunkten
PK ist statisch äquivalent zu
- der Einzelkraft
r
O
FK 
K
PK
n
F
k 1
K
in O und
- dem Momentenvektor
n
MK
M   M K , M K  rK  FK
k 1
rK  OPK
F greift in O an, ist aber unabhängig von der Wahl von O
-M hat keinen Angriffspunkt, hängt aber von der Wahl von O ab
--
1.6 Gleichgewicht des starren Körpers
Gleichgewicht:
Körper ist in Ruhe und bleibt in Ruhe.
n
Statisch Äquivalent: F   FK in O
k 1
n
und : M   rK  FK , rK  OPK
k 1
Gleichgewichtsbedingungen für starren Körper
n
F
„Kräftegleichgewicht“:
n
r
„Momentengleichgewicht“:
k 1
0
K
k 1
K
 FK  0 , rK  OPK , O beliebig wählbar
In Komponenten
n
F
Kräfte:
k 1
XK
n
 r
Momente:
k 1
YK
n
 r
k 1
ZK
n
 r
k 1
XK
0,
n
F
k 1
YK
n
 0 ,  FZK  0
k 1
FZK  rZK FYK   0
FXK  rXK FZK   0
FYK  rYK FXK   0
gilt für die (x,y)-Ebene
Beispiel
x
l
G1
G2
Schnittbild/Feinschnitt
F
O’
x
O
l
G2
G1
Gleichgewicht
der Kräfte:
→:0
↑ : F - G1 - G2 = 0
der Momente
O : Fx – Gsl
=0
daraus lässt sich folgendes ablesen
für einen anderen Bezugspunkt O’
F = G1 + G2
O’: G1x – G2 (l – x) = 0
(G1 + G2) x
= G2l
G2 l
x
G1  G2
x
G2 l
G2 l

F
G1  G2
Momente einer Kraft
M  r F
F
O
r


P
a
M  rF sin 
 Fa
a = „Hebelarm“
(Bei ebenen Problemen)
Erstarrungsprinzip
Befindet sich ein mechanisches System unter dem Einfluss eines Kräftesystems im
Gleichgewicht, so erfüllt es dieselben Gleichgewichtsbedingungen wie ein starrer Körper.
Das System darf im Gleichgewicht als erstarrt angesehen werden.
Schnittprinzp
Ist ein mechanisches System im Gleichgewicht, so ist auch jedes Teilsystem im
Gleichgewicht. Das an das Teilsystem angreifende Kräftesystem besteht aus:
- den äußeren Kräften, die an dem Teilsystem angreifen und
- den Schnittkräften, die der Rest des Systems auf das Teilsystem ausübt.
Gegenwirkungsprinzip
Üben zwei Körper (oder Teile eines Körpers) Kräfte aufeinander aus, so haben diese dieselbe
Wirkungslinie und sind gleich groß, aber entgegengesetzt gerichtet.
Schnittbild
Gleichgewichtsbedingungen
Kräfte
→
(1)
F2 cos   F  0
l
↑
h
cos 

F2
Momente
h
A
A
G
l
sin 
2
(2)
(1)
F1
l
sin  cos 
2h
l
F  G sin  cos 2 
2h
F2  G
F1  G  F2 sin 
 G (1 
1
h
G  sin   F2
(3)
2
cos 
F
Sofort ausrechnen aus
(3)
F2 sin   F1  G  0 (2)
l
sin 2  cos  )
2h
Bedingung für (1)
F1  0
l
sin 2  cos   0
2h
l
1
sin 2  cos 
2h
l
sin 2  cos   1
2h
2h
l
2
sin  cos 
1
Gleichgewichtsaufgaben
1. System abgrenzen
2. Alle Kräfte einzeichnen, die auf das System einwirken
3. Orthogonale Richtungen für das Kräftegleichgewicht und Bezugspunkt für das
Momentengleichgewicht festlegen.
4. Gleichgewichtsbedingungen formulieren
5. Nach den unbekannten Kräften auflösen.
2. Gewichtskraft und Schwerpunkt
2.1 Verteilte Kräfte
Gegensatz: konzentrierte Kraft, Einzelkraft
Volumenkraft
B
Vi
Vi
Teilvolumina
f i Vi
fi
Kraft pro Volumen
N 
 m 3 
ri
Anzahl  
Gesamtkraft
F   f i Vi
i
Gesamtmoment
M 0   ri  f i Vi
Grenzübergang
Vi  0 gleichmäßig
i
F   f dv
B
M 0   r  f dV
B
B
dV
Volumenelement dV
F   f dV
B
f dV
Volumenkraftdichte f