W. Kley: Planetenentstehung (WS 2012/13)

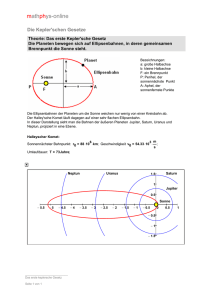
Planetenentstehung
2. Kapitel: Das Sonnensystem
Wilhelm Kley
Institut für Astronomie & Astrophysik
Abtlg. Computational Physics
Wintersemester 2012/13
W. Kley:
Planetenentstehung (WS 2012/13)
2. Sonnensystem
Übersicht
2.1 Objekte im Sonnensystem
2.2 Planetenbahnen
2.3 Physikalische Eigenschaften der Planeten
2.4 Zwergplaneten und Kleinkörper
2.5 Chronologie im frühen Sonnensystem
2.6 Zusammenfassung
W. Kley:
Planetenentstehung (WS 2012/13)
1
2.1 Objekte
Übersicht
2.1 Objekte im Sonnensystem
W. Kley:
Planetenentstehung (WS 2012/13)
2
2.1 Objekte
Antike Kenntnis
• 1 Stern (Sonne)
• 6 Planeten
- Merkur, Venus, Erde, Mars, Jupiter, Saturn
• 1 Mond (Satellit der Erde)
W. Kley:
Planetenentstehung (WS 2012/13)
3
2.1 Objekte
Uranus (1781)
William Herschel
(1738-1822)
W. Kley:
Planetenentstehung (WS 2012/13)
4
2.1 Objekte
Adams / Le Verrier
John Couch Adams
(1819-1892)
Urbain Jean Joseph Le Verrier
(1811-1877)
Perihelshift Merkur
Berechnung der Uranus-Störungen −→ weiterer Planet (1841-1845)
W. Kley:
Planetenentstehung (WS 2012/13)
5
2.1 Objekte
Neptun (1846)
Johann Gottfried Galle
(1812-1910)
W. Kley:
Planetenentstehung (WS 2012/13)
6
2.1 Objekte
Ceres (1801)
Giuseppe Piazzi
(1746-1826)
Größter Asteroid
Zwischen Mars-Jupiter
W. Kley:
Planetenentstehung (WS 2012/13)
7
2.1 Objekte
Pluto (1930)
Clyde Tombaugh
(1906-1997)
Mond: Charon (1978)
Monde: S/2005 P1 und S/2005 P2
(Nix, Hydra)
(Mai 2005, HST, Hubble Space Telescope)
W. Kley:
Planetenentstehung (WS 2012/13)
8
2.1 Objekte
QB1: Erstes TNO
TNO: Trans-Neptunisches Objekt
August 1992
D. Jewitt, Univ. of Hawaii
R = 22.8 mag
a = 37 - 59 AE
d = 200 km
W. Kley:
Planetenentstehung (WS 2012/13)
9
2.1 Objekte
Aktueller Überblick
a) Ein Stern, die Sonne
b) 4 erdähnliche, terrestrische oder Innere Planeten
(Merkur, Venus, Erde, Mars), 0.39-1.6 AE
c) 4 große gasreiche Planeten, jovianische, Äußere Planeten
(Jupiter, Saturn, Uranus, Neptun), 5 - 30 AE
d) Asteroiden zwischen Mars und Jupiter, 2.2 bis 3.2 AE,
auch bei gleichen Orbits wie Planeten in sog. 1:1 Resonanz
und zwischen den einzelnen Planeten möglich
e) Satellitensysteme (Monde) um die Planeten,
bis auf Merkur und Venus
f) Kometen (kurzper.) und transneptunische Objekte (TNOs), einschließlich Pluto, die den sog. Kuiperbelt bevölkern
g) Oortsche Wolke, bis etwa 104 AE, Ursprung der langperiodischen Kometen
h) Größere Mengen an Gas und Staub (Zodiaklicht)
W. Kley:
Planetenentstehung (WS 2012/13)
10
2.1 Objekte
Mythologie
a) Merkur Röm. Gott des Handels, der Reisenden und der Diebe,
(röm. Gegenstück zu Hermes, dem Götterboten)
b) Venus Gr. Aphrodite, Göttin der Liebe und Schönheit, dritthellstes Objekt am Himmel, Morgen- Abendstern (Eosphorus,
Hesperus).
c) Jupiter röm. König der Götter, Herrscher über den Olymp,
griech. Zeus, Sohn des Chronos (Saturn)
d) Saturn röm. Mythologie, Gott des Ackebaus, (Griech. Chronos), Sohn von Gaia und Uranus, Vater von Zeus.
e) Uranus Gottheit der Himmel, Sohn und Geliebter von Gaia, Vater von Chronos (Saturn), der Zyklopen und Titanen.
f) Neptun röm. Gott des Meeres (gr. Poseidon)
g) Pluto (Griech. Hades) Gott der Unterwelt, Soweit von der Sonne entfernt, dadurch in ewiger Dunkelheit
h) Charon Griech. Myth.: Fährmann, der die Toten über den Styx
in den Hades bringt.
W. Kley:
Planetenentstehung (WS 2012/13)
11
2.2 Planetenbahnen
Übersicht
2.2 Planetenbahnen
- Keplergesetze
- Bewegungsgleichungen (Zweikörperproblem)
- Bahneigenschaften
- Planeten des Sonnensystems
- Bahnelemente der Planeten
W. Kley:
Planetenentstehung (WS 2012/13)
12
2.2 Planetenbahnen
Keplergesetze
1) Die Planeten bewegen sich auf elliptischen Bahnen, wobei die
Sonne sich in einem Brennpunkt der Ellipse befindet
2) Die Verbindungslinie Sonne-Planet überstreicht gleiche Flächen
in gleichen Zeiten
3) Das Quadrat der Bahnperiode (P) ist proportional zum Kubus
des mittleren Abstandes (Grosse Halbachse a) von der Sonne.
W. Kley:
Planetenentstehung (WS 2012/13)
13
Relativkoordinaten
2.2 Planetenbahnen
P
r
S
rp
r
s
O
O: Koordinatenursprung
S: Sonne, ~r s Radiusvektor zur Sonne
P: Planet, ~r p Radiusvektor zum Planeten
~r = ~r p − ~r s Vektor von Sonne zum Planeten
W. Kley:
Planetenentstehung (WS 2012/13)
14
2.2 Planetenbahnen
Das Zweikörperproblem
Das Zweikörperproblem kann auf ein äquivalentes Einkörperproblem für die Relativbewegung reduziert werden
~r
¨
µ~r = − GM µ 3
r
(1)
Der Planet bewegt sich wie ein Körper der reduzierten Masse
µ = Msmp/(Ms + mp) im Feld der Zentralmasse M = Ms + mp.
~r ist der Relativvektor, ~v = ~r˙ die Relativgeschwindigkeit.
Erhaltungsgrößen :
Energie
Mµ
1 2
E = µv − G
2
r
(2)
~ = µ~r × ~v
L
(3)
Drehimpuls
W. Kley:
Planetenentstehung (WS 2012/13)
15
2.2 Planetenbahnen
Bewegungsgleichungen
~ (Drehimpuls/Masse)
Spezifischer Drehimpuls h
~
~ ≡ µh
L
~ ⊥ ~r , d.h. Bewegung in Ebene senkrecht zu L.
~
Es gilt h
~ also h = Lz /µ
Wähle KO-System mit z-Achse parallel zu L,
x = r cos φ,
y = r sin φ
Die Bewegungsgleichung (1) lautet nun
r2φ̇ = h
r̈ − rφ̇
2
k
= − 2
r
(4)
(5)
mit k = G M .
W. Kley:
Planetenentstehung (WS 2012/13)
16
Flächensatz
2.2 Planetenbahnen
1111111111111111
0000000000000000
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
dr
Fläche dS des
schraffierten Dreiecks
xx
r
O
1
~
dS = |~r × dr|
2
teile durch dt
1
Ṡ = |~r × ~v |
2
mit (4)
1
Ṡ = h
2
(6)
d.h. Drehimpulserhaltung ⇒ Zweites Keplersches Gesetz
W. Kley:
Planetenentstehung (WS 2012/13)
17
2.2 Planetenbahnen
Radial-Gleichung
Einsetzen der Drehimpulsgleichung ergibt (k = GM )
h2
k
r̈ + 2 − 3 = 0
r
r
(7)
Multiplikation mit ṙ und Integration über die Zeit t liefert
1 2 k
h2
ṙ − + 2 = 2
r 2r
(8)
= E/µ spezifische Energie (Energie/Masse) des Planeten
Definiere effektives Potential
W. Kley:
h2
k
Veff (r) = − + 2
r 2r
(9)
ṙ2 + 2Veff (r) = 2
(10)
Planetenentstehung (WS 2012/13)
18
2.2 Planetenbahnen
Effektives Potential
Veff (r)
ε3
r
O
ε2
ε1
W. Kley:
Kreisbahn
Ellipse
Parabel
Hyperbel
Zentrifugalpotential:
für r → 0 abstoßend.
ε0
r0
= 0
< 1 < 0
= 2 = 0
= 3 > 0
k
h2
Veff (r) = − + 2
r 2r
(gebunden)
(gebunden)
(marginal gebunden)
(ungebunden)
Planetenentstehung (WS 2012/13)
19
Die Form der Bahn
2.2 Planetenbahnen
dr dφ
1
Mit ṙ =
und u =
dφ dt
r
2
du
2ku 2
2
⇒
+u − 2 = 2
dφ
h
h
nochmal ableiten: ⇒ Binet’s Gleichung:
d2u
k
+u= 2
2
dφ
h
(11)
(inhomogene Oszillatorgleichung)
p
r=
1 + e cos(φ − φ0)
Die Lösung lautet:
(12)
Gleichung für Kegelschnitt = 1. Keplersches Gesetz
in Gl.11
W. Kley:
⇒
e=
2
2h
1+ 2
k
1/2
Planetenentstehung (WS 2012/13)
h2
,p=
≡ a(1 − e2)
k
(13)
20
Die Ellipse
2.2 Planetenbahnen
F Fokus (Sonne)
P Planet
semi lactus rectum
p = a ( 1 − e 2 ) r (Abstand: F-P)
a große Halbachse
b kleine (b ≤ a)
P
b
r
E
Aphel
a
O
φ
F
Perihel
Exzentrizität
e = (1 − b2/a2)1/2
q = a(1 − e) (Perihel)
Q = a(1 + e) (Aphel)
φ wahre Anomalie
q=a(1−e)
( Winkel: Perihel - Planet)
E: exzentrische Anomalie
W. Kley:
Planetenentstehung (WS 2012/13)
21
2.2 Planetenbahnen
Energie und Drehimpuls
Im Perihel rp und Aphel ra ist v ⊥ r, also gilt
L = µrpvp = µrava
1 2 GM µ
1 2 GM µ
E = µvp −
= µva −
2
rp
2
ra
mit rp = a(1 − e) und ra = a(1 + e) folgt (NOTE: L = µh, E = µ)
p
L = µ GM a(1 − e2),
GM µ
E=−
2a
(14)
Integriere Flächensatz (6) über ganze Periode P : πab/P = h/2
p
mit b = a (1 − e2)
2 3
4π
a
2
P =
GM
d.h. Das Dritte Keplersche Gesetz
W. Kley:
Planetenentstehung (WS 2012/13)
(15)
22
2.2 Planetenbahnen
Der Planet in der Bahn I
Die radiale Bewegungsgleichung lautete (8)
2B C
+ 2
ṙ = A +
r
r
2
(16)
C = −h2
(17)
Zr
Zt
dr
q
allg. Lsg.
= dt
(18)
2B
C
A
+
+
r0
t0
r
r2
1/2
AC
B
e= 1− 2
Substitution
r = a (1 − e cos E) a = −
A
B
Lsg.: (mit Perihel bei t = 0) Kepler Gleichung
mit A = 2,
B = k,
2π
M = t = E − e sin E
P
(19)
M mittl. Anomalie, P Periode., E = 0 Perihel, E = π Aphel.
W. Kley:
Planetenentstehung (WS 2012/13)
23
2.2 Planetenbahnen
Der Planet in der Bahn II
Kepler-Gleichung ist transzendente Gleichung, Lösung iterativ
starte zu einer festen Zeit (eg. t = P/4) mit Anfangswert E0 (eg. π/2),
und iteriere
Ek+1 = M + e sin Ek
(20)
Berechne wahre Anomalie φ mit
r
φ
1+e
E
tan
=
tan
2
1−e
2
(21)
und Abstand r nach (12)
p
r=
1 + e cos(φ − φ0)
W. Kley:
Planetenentstehung (WS 2012/13)
24
2.2 Planetenbahnen
Dimensionen im Sonnensystem
Größe
Äquatorialer Erdradius
Sonnenparallaxe
Astronomische Einheit (AE)
(große Halbachse der Erde)
Lichtgeschwindigkeit
Lichtlaufzeit für 1 AE
mittl. Bahngeschw. der Erde
Symbol
R♁
π
a♁ = R♁/π
c
a♁/c
v̄♁
Wert
6.378 · 106 m
8.794”
1.496 · 1011 m
2.9979 · 108 m/s
499.0 s
2.98 · 104 m/s
Sonnenparallaxe: ∠ des Erdradius von Sonne aus betrachtet.
vgl. Sonnenradius: 6.98 · 108 m
W. Kley:
Planetenentstehung (WS 2012/13)
25
2.2 Planetenbahnen
Planetenbewegung
Umlaufzeiten:
siderische: Wahre Umlaufzeit P eines Planeten um die Sonne
synodische: Umlauf relativ zur Sonne,
Psyn Zeit zwischen 2 Konjunktionen
Mittlere Bahngeschwindigkeiten:
Relativgeschwindigkeit:
nerde, nplanet
nerde − nplanet = 2π/Psyn
Für äußere Planeten (nerde > nplanet )
1
1
1
=
−
Psyn Perde Pplanet
Beispiel Mars Psyn = 2.14 Jahre
W. Kley:
Planetenentstehung (WS 2012/13)
26
2.2 Planetenbahnen
Bahnelemente I
Vollständige Beschreibung der Bahn durch:
- 2 Bahnelemente a, e (Große Halbachse, Exzentrizität)
- 3 Winkel, welche die Orientierung der Bahn angeben
- 1 Zeitursprung TP, z.B. der Durchgang durch Perihel
Referenzkoordinatensystem:
Kartesisches System: Im Ursprung die Sonne
x − y Ebene = Ekliptikebene = Ebene der Erdbahn
z-Achse in Richtung des Drehimpulse der Erdbahn
x-Achse in Richtung des aufsteigenden Knotens der Erdbahn,
(Frühlingspunkt (-Äquinoktium, Tag- und Nachtgleiche), Widderpunkt)
W. Kley:
Planetenentstehung (WS 2012/13)
27
2.2 Planetenbahnen
Bahnelemente II
a,e
Frühlingspunkt
Knoten :
aufsteigender
absteigender
i Inklination
∠ Erdbahn-Eklipt.
Ω Länge des
aufsteig. Knotens
in Ekliptik
ω Länge des
Perihels vom in Bahnebene
TP Periheldurchgang
W. Kley:
Planetenentstehung (WS 2012/13)
28
2.2 Planetenbahnen
Bahnelemente III
Mit allen 6 Größen a, e, i, Ω, ω, TP ist
eindeutige Bestimmung des Position des Planeten möglich
Damit können z.B. die Orte ~r und die Geschwindigkeiten ~v des
Planeten eindeutig angegeben werden.
Bewegungsgleichungen (9 Körper, Sonne + 8 Planeten)
~ri
¨
~i, i = 1, ..., 9
~ri = −GMi
+
F
|~ri|3
(22)
F~i Störungen der anderen Körper auf i-ten Planeten (Masse mi)
Mi = (M + mi)
Gl. nicht exakt lösbar, näherungsweise Ellipsen plus Störungen
⇒ Variation der Bahnelemente (oskulierende Elemente)
z.B. variiert e♁ zwischen 0 und 0.06, heute 0.0167
W. Kley:
Planetenentstehung (WS 2012/13)
29
2.2 Planetenbahnen
W. Kley:
Überblick: Sonnensystem
Planetenentstehung (WS 2012/13)
30
2.2 Planetenbahnen
Bahnelemente der Planeten
Momentane Bahnelemente der Planeten
Name
Symb. Gr. Halbachse
a [AU]
Merkur '
0.3871
Venus ♀
0.7233
Erde
1.0000
♁
Mars
1.5237
♂
Ceres
2.766
Jupiter X
5.2026
Saturn Y
9.5549
Uranus Z
19.2184
Neptun [
30.1104
Pluto
\
39.5447
Exzent. Inklin.
e
Grad
0.2056
7◦000
0.0068
3◦240
0.0167
0.0934
1◦510
0.077
10◦400
0.0488
1◦180
0.0555
2◦290
0.0463
0◦460
0.0090
1◦460
0.2490 17◦090
Periode
[Jahre]
0.241
0.615
1.00
1.88
4.601
11.9
29.5
84.0
165
248
Die Bahnelemente variieren (oskulieren) aufgrund der Wechselwirkungen untereinander
W. Kley:
Planetenentstehung (WS 2012/13)
31
2.2 Planetenbahnen
Titius-Bode
rn = 0.4 + 0.3 · 2n (Johann Titius 1766)
Name
Nummer
Merkur
Venus
Erde
Mars
Ceres
Jupiter
Saturn
Uranus
Neptun
Pluto
0
1
2
3
4
5
6
7
-
Titius-Bode
an
0.4
0.7
1.0
1.5
2.8
5.2
9.6
19.2
30.1
-
Polyeder
aK
0.373
0.785
1.0
1.411
4.858
9.342
-
Beobachtet
a
0.4
0.7
1.0
1.5
2.8
5.2
10.0
19.6
38.8
39.5
Veröffentlicht im Astronomische Jahrbuch 1772 durch Bode
Übereinstimmung mit den Daten von Uranus (n = 6) und Ceres (n = 3)
Diente Adams und Leverrier zum Auffinden von Neptun
Passt innen und außen nicht: Starke Kritik u.a. von Gauss
Polyeder (fünf platonische Körper) von Kepler 1596
W. Kley:
Planetenentstehung (WS 2012/13)
32
2.2 Planetenbahnen
Resonanzen
Einige der Umlaufzeiten der Planeten stehen (fast !) im Verhältnis zweier ganzer Zahlen, d.h. sie sind kommensurabel.
Planeten
Jupiter-Saturn
Saturn-Uranus
Uranus-Neptun
Neptun-Pluto
P1/P2
0.403
0.351
0.509
0.665
Resonanz
2:5
1:3
1:2
2:3
Andere Formulierung:
5nS − 2nJ = 0.007127/Jahr
2nN − 3nP = 0.000159/Jahr
(23)
(24)
ni mittlere Bewegung (Winkel/Zeit) der Planeten in der Bahn.
Perihel von Pluto ist kleiner als das von Neptun: Orbitcrossing
Aber: Perihels liegen etwa 180◦ auseinander.
D.h. die Neptun und Pluto kommen sich niemals nahe.
W. Kley:
Planetenentstehung (WS 2012/13)
33
2.2 Planetenbahnen
Neptun und Pluto I
Umlaufzeiten:
Neptun: 165 Jahre
Pluto:
248 Jahre
Abstand (Gr. Halbachse):
Neptun: 29.76 AE
Pluto:
39.5 AE
Exzentrizität:
Pluto:
0.25
⇒ Kreuzende Bahnen !!
Stabilisierung durch:
(α-Centauri, BR-Online)
W. Kley:
Planetenentstehung (WS 2012/13)
3:2 Resonanz
Neptun 3 Umläufe
Pluto 2 Umläufe
34
2.2 Planetenbahnen
Neptun und Pluto II
Planetenbahnen:
im mitrotierenden System
von Neptun
Pluto
Neptun
Uranus
Saturn
(Gravity Simulator, Tony Dunn)
W. Kley:
Planetenentstehung (WS 2012/13)
35
2.2 Planetenbahnen
Masse und Drehimpuls
Massen: M = 2 × 1030 kg, MPlaneten = 2.7 × 1027 kg
Massenanteile: Wasserstoff: X = 0.73, Helium: Y = 0.25, Metalle: Z = 0.02
Sonne hat mehr Masse in schweren Elementen als alle Planeten zusammen
Drehimpuls:
Sonnenrotation: 25.4d am Äquator, 36d am Pol, im Innern 27 Tage
Der Spindrehimpuls der Sonne (Neigung um 7◦ gegen Ekliptik)
2
L = αMR
Ω = α 2.5 × 1042 kg m2 s−1
(25)
α ist der Faktor des Trägheitsmoments.
Für zentrale Dichte 100 mal der mittleren: α ≈ 0.055 (homog. Kugel 0.4).
Bahndrehimpuls der Planeten:
q
√
Li = mi µia(1 − e2i ) = mi µipi
(26)
Die vier großen Planeten ergeben LP = 3.13 × 1043 kg m2 s−1.
D.h. die Sonne hat 99.86% der Masse, aber nur 0.5% des Gesamtdrehimpulses.
W. Kley:
Planetenentstehung (WS 2012/13)
36