Institut für Physik und Werkstoffe

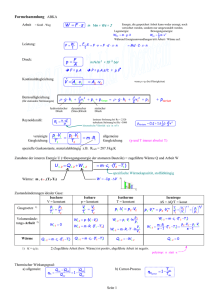
Fachhochschule Flensburg
Fachbereich Technik
Institut für Physik und Werkstoffe
Name:
Name :
Versuch-Nr:
W1
Äquivalenz von Wärme und Arbeit
Gliederung:
Seite
1. Einleitung
2. Äquivalenz von mechanischer Arbeit und Wärme
2.1. Methode
2.2. Versuchsdurchführung
2.3. Auswertung
3. Äquivalenz von elektrischer Arbeit und Wärme
3.1. Methode
3.2. Versuchsdurchführung
3.3. Auswertung
Semester:
1
2
3
4
4
5
6
.....................................
Unterschrift des/der Studenten
Als Übungsergebnis anerkannt:
Flensburg, den .......................
.....................................
Unterschrift des Dozenten
Labor für Physik
Versuch :
W1
Blatt:
1
1. Einleitung
In diesem Versuch soll am Beispiel von mechanischer und elektrischer Arbeit gezeigt
werden, dass Wärme und Arbeit äquivalent sind. Details zu den einzelnen Messungen
sind in den Abschnitten 2 und 3 beschrieben.
Energie und Arbeit sind wichtige Größen, um technische und physikalische Vorgänge
zu charakterisieren. Allgemein beschreibt die Energie als eine Zustandsgröße die
Fähigkeit eines Systems, Arbeit zu verrichten.
Der
physikalische
Arbeitsbegriff
entwickelte
sich
aus
dem
Studium
der
Kräfteübertragung durch z.B. Hebel oder Getriebe. Mittels mechanischer Geräte
ließen sich Kräfte transformieren. Das Produkt Kraft × Weg erwies sich jedoch bei
allen Vorgängen als eine Konstante. Der so definierte Begriff der mechanischen Arbeit
ließ sich sehr vielseitig anwenden, um Wirkungen von Kräften zu charakterisieren
und zu vergleichen. Ein erweitertes Konzept der physikalischen Arbeit ließ sich auf
elektrische und thermische Vorgänge übertragen.
Eine wichtige Rolle spielt in diesem Zusammenhang das Verhältnis zwischen Arbeit
und Energie.
- Energieerhaltungssatz: In einem energetisch abgeschlossenem System ist die
Energie konstant.
- Wird an einem System Arbeit verrichtet, ändert sich dessen Energie um den Betrag
der verrichteten Arbeit.
Die an einem Körper (System) verrichtete mechanische oder elektrische Arbeit muss
dann grundsätzlich zu einer entsprechenden Änderung der Wärmeenergie, der
inneren Energie U dieses Körpers führen. Dabei sind die Versuchsbedingungen so zu
gestalten, dass die verrichtete Arbeit vollständig in Wärme umgewandelt wird und
auf anderem Wege kein weiterer Energieaustausch stattfindet.
W = ∆U = C ⋅ ∆T
(1.1)
Die innere Energie U und die Temperatur sind nach den Gesetzen der
Thermodynamik einander proportional. Als Proportionalitätskonstante existiert die
für jeden Körper spezifische Wärmekapazität C ([C]=J/K).
Für die Einheiten der Größen Arbeit und Energie gilt:
kgm 2
[W ] = [U ] = 2 = Nm = J = Ws
s
(1.2)
Labor für Physik
Die Einheiten
gleichwertig.
Versuch :
W1
Blatt:
2
ksm 2
, Nm (Newtonmeter), J (Joule) und Ws (Wattsekunden) sind alle
s2
2. Äquivalenz von mechanischer Arbeit und Wärme
2.1 Methode
Die Messung erfolgt dadurch, dass Reibungsarbeit vollständig in Wärme überführt
wird.
Um ein mit Wasser gefülltes kupfernes Kalorimetergefäß ist mehrfach ein
Kunststoffband geschlungen. Dessen freies Ende wird mit einer Masse von 5 kg
belastet. Das andere Ende wird von einer Federwaage gehalten. Im Kalorimetergefäß
befindet sich eine abgewogene Menge Wasser, deren Temperatur mit einem
Thermometer gemessen werden kann. Man dreht das Kalorimetergefäß gerade so
schnell, dass die Federwaage entlastet ist. Die Reibungskraft zwischen Kupfergefäß
und Kupferband ist nun genau gleich der Gewichtskraft der 5kg-Masse.
Die verrichtete mechanische Arbeit beträgt:
Wmech = FG ⋅ s = mG ⋅ g ⋅ π ⋅ d ⋅ n
(2.1)
Labor für Physik
Versuch :
W1
Blatt:
3
mG = 5kg : Masse des Gewichts, d: Durchmesser des Kupfergefäßes, n: Anzahl der
Umdrehungen
Diese Arbeit erwärmt das Wasser, das Gefäß und das Thermometer um den Betrag
∆T = TE − T A .
Q = ∆U = (CThermometer + mCu ⋅ cCu + mW ⋅ cW ) ⋅ ∆T
Wärmekapazität des Thermometers: CThermometer = 3,55 ⋅ 10 −3
spezifische Wärmekapazität von Kupfer: cCu = 0,383
spezifische Wärmekapazität vom Wasser
kJ
K
kJ
,
kgK
,
(2.2)
Die Beträge von mechanischer Arbeit und Wärme sollen gleich sein, d.h. ihr
Verhältnis Aergibt den Wert 1.
A=
Wmech
mG ⋅ g ⋅ π ⋅ d ⋅ n
=
Q
(CThermometer + mCu ⋅ cCu + mW ⋅ cW ) ⋅ ∆T
(2.3)
2.1 Versuchsdurchführung
Der Versuch sollte nach folgendem Schema ablaufen:
1. Durchmesser des Kalorimeters bestimmen. Wiegen des Kalorimetergefäßes
mit Verschraubung
2. Kalorimetergefäß mit Wasser füllen (ca. 50 – 60 g) und erneut wiegen
3. Thermometer einsetzen und verschrauben. Apparatur zusammensetzen
(Kunststoffband 3 bis 4 mal um das Kalorimeter schlingen)
4. Anfangstemperatur TA des Kalorimeters ablesen
5. Langsam kurbeln (ca. 2 Umdrehung/s), Anzahl der Umdrehungen zählen
6. Endtemperatur TE des Kalorimeters ablesen
Hinweise: Es wird empfohlen, eine Temperaturspreizung ∆T von 5 bis 6 K zu
erreichen. Die Anfangstemperatur des Kalorimeters sollte um den Betrag
unter der
Raumtemperatur liegen, die Endtemperatur um den gleichen Betrag darüber. So
werden Fehler durch Wärmeaustausch mit der Umgebung vermieden: Wärmezufuhr
und Wärmeabfuhr kompensieren sich gerade.
Labor für Physik
Versuch :
W1
Blatt:
4
2.2 Auswertung
1. Durchführen des Versuchs wie in 2.2 beschrieben und die Messwerte in dem
beiliegenden Formular protokollieren.
2. Messfehler für alle gemessenen Größen abschätzen
3. Verhältnis A =
Wmech
ermitteln
Q
4. Führen Sie auf der Grundlage der Gleichung 2.3 eine Fehlerfortpflanzungsrechnung
nach Gauss durch
5. Erklären und bewerten Sie evtl. Abweichungen vom idealen Wert A=1
6. Diskutieren Sie Versuch, Versuchsablauf und Ergebnis. Ist Ihnen etwas aufgefallen?
3. Äquivalenz von elektrischer Arbeit und Wärme
3.1 Methode
Die Äquivalenz von elektrischer Arbeit und Wärme wird in diesem Versuch dadurch
bestimmt, dass man die in einem stromdurchflossenen Leiter entwickelte Joulsche
Wärme kalorimetrisch misst. Als Leiter dient hier ein Tauchsieder. Die elektrische
Arbeit wird direkt durch einen Kilowattstundenzähler gemessen. Der Tauchsieder
erwärmt ein mit Wasser gefülltes Kalorimeter. Die Wärmekapazität des Gefäßes
selbst beträgt C K = (0,28 ± 0,015) kJ K
Die im Tauchsieder umgesetzte elektrische Arbeit beträgt:
Wth = U eff ⋅ I eff ⋅ t ⋅ η el = Wel ⋅ η el
(3.1)
Labor für Physik
Die abgelesene Arbeit WE muss
Versuch :
W1
Blatt:
5
um den elektrischen Wirkungsgrad η el = 0,994
korrigiert werden. Damit werden Verluste in den Zuleitungen und im kWh-Zähler
selbst berücksichtigt.
Die Temperatur des gesamten Kalorimeters steigt beim Heizen um ∆T = TE − T A .
Q = ∆U = (C K + cW ⋅ mW ) ⋅ ∆T
(3.2)
Die Beträge von elektrischer Arbeit und Wärme sollten gleich sein, d.h. ihr Verhältnis
A ergibt den Wert 1.
A=
Wth
Wel ⋅ η el
=
Q (C K + cW ⋅ mW ) ⋅ ∆T
(3.3)
3.2 Versuchsdurchführung
1. Kalorimetergefäß mit Wasser füllen. Masse mW der Wasserfüllung feststellen,
indem das volle mit dem leeren Gefäß verglichen wird.
2. Anfangswerte von Temperatur und Zählerstand ablesen.
3. Wasser unter ständigem Mischen auf ca. 70°C erhitzen.
4. Endwerte von Temperatur und Zählerstand ablesen.
Hinweise:
Der Kilowattstundenzähler kann auf der Strichskala auf eine Wattstunde genau
abgelesen werden.
Bei den Punkten b und d ist zu berücksichtigen, dass die Messungen der
Temperaturen nur zuverlässig sind, wenn Dewargefäß, Wasser, Tauchsieder und
Thermometer die gleiche Temperatur haben. Dieser Temperaturausgleich stellt sich
erst mit der Zeit ein. Sowohl die Anfangs- als auch die Endtemperatur sollten daher
mittels einer Messreihe bestimmt werden. Dabei geht man folgendermaßen vor:
Beginnend fünf Minuten vor dem Einschalten wird die Wassertemperatur im
Halbminutentakt (genau!) gemessen. Der zeitliche Verlauf der Temperatur wird
grafisch aufgetragen und durch eine Gerade approximiert (grafisch optimal nach
Augenmaß oder rechnerisch mittels Linearer Regression mit Hilfe eines geeigneten
Programms oder eines Taschenrechners). Extrapoliert man diese Gerade bis zum
Einschaltpunkt, erhält man die Anfangstemperatur TA.
Labor für Physik
Versuch :
W1
Blatt:
6
Temp.
Extrapolierter Temperaturwert
Zeit
Die Endtemperatur TE bestimmt man entsprechend: Nach dem Ausschalten weiter
mischen! Etwa eine Minute nach dem Ausschalten der Heizung beginnt man, die
Temperatur im Halbminutentakt zu messen. Die approximierte Gerade wird
rückwärts zum Ausschaltpunkt extrapoliert und liefert so den gewünschten
Temperaturwert.
3.3 Auswertung
1. Durchführen des Versuchs wie in 3.2 beschrieben und die Messwerte in dem
beiliegenden Formular protokollieren.
2. Messfehler für alle gemessenen Größen abschätzen
3. Verhältnis A =
4. Führen
Sie
Wth
ermitteln
Q
auf
der
Grundlage
der
Fehlerfortpflanzungsrechnung nach Gauss durch
Gleichung
3.3
5. Erklären und bewerten Sie evtl. Abweichungen vom idealen Wert A=1
eine
6. Diskutieren Sie Versuch, Versuchsablauf und Ergebnis. Ist Ihnen etwas
aufgefallen?
Labor für Physik
Versuch : W1
Anlage A
Anmerkungen :
Dieser Vordruck ist von jedem Studenten während der Versuchsdurchführung mit
Tinte oder Kugelschreiber auszufüllen. Tragen Sie übersichtlich die gemessenen
Werte und die abgeschätzten Messfehler ein.
Diese Vordrucke sind zusammen mit den Laborberichten abzugeben.
----------------------------- -------------------------- --------------------------- -----------------------------Student
Studiengruppe
Datum
Laboringenieur
Tragen Sie hier Ihre Messwerte in die Tabelle ein:
Messwerte:
Kupfermenge (Kalorimeter + Verschraubung)
mCu
kg
Kupfermenge+Wassermenge
mges
kg
Wassermenge mges - mCu
mW
kg
Wägestück
mG
Raumtemperatur
5
kg
°C
Anfangstemperatur
TA
°C
Endtemperatur
TE
°C
Temperaturdifferenz TE – TA
∆T
°C
Anzahl der Umdrehungen
N
Kalorimeterdurchmesser
D
Abgeschätzte Messunsicherheiten:
m
Labor für Physik
Versuch : W1
Anlage B
Anmerkungen :
Dieser Vordruck ist von jedem Studenten während der Versuchsdurchführung mit
Tinte oder Kugelschreiber auszufüllen. Tragen Sie übersichtlich die gemessenen
Werte und die abgeschätzten Messfehler ein.
Diese Vordrucke sind zusammen mit den Laborberichten abzugeben.
----------------------------- -------------------------- --------------------------- -----------------------------Student
Studiengruppe
Datum
Laboringenieur
Masse des leeren Kalorimeters
mK
kg
Masse des Kalorimeters mit Wasser
mges
kg
Wassermenge mges – mK
mW
kg
Anfangstemperatur des Wassers
TA
°C
Endtemperatur des Wassers
TE
°C
Temperaturdifferenz TE – TA
∆T
°C
Anfangsstand des kWh-Zählers
WA
kWh
Endstand des kWh-Zählers
WE
kWh
Zugeführte elektr. Energie WE - WA
∆W
kWh
Abgeschätzte Messunsicherheiten: