Kapitel III Arbeit, Leistung und Energie

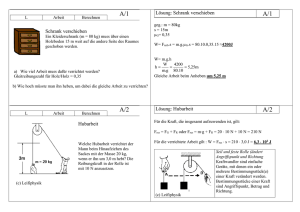
Kapitel III Arbeit, Leistung und Energie
3.1 Arbeit
Betrachtet man die Momentaufnahme eines Gewichtsstück,
welches an einem Kran hängt, so kann man an den Kräften
zunächst nicht unterscheiden, ob die Last in Ruhe ist oder sich
gleichförmig bewegt. Nach dem Trägheitsgesetz sind
Zugkraft und Gewichtskraft in beiden Fällen im
Gleichgewicht! (Nur beim Beschleunigen des Gewichtes wäre
FZ grösser)
Für die Seilwinde sind aber beide Fälle vollkommen
unterschiedlich: Während man im ersten Fall (also bei Ruhe)
den Motor im Prinzip ausschalten kann (das Seil lässt sich
auch mit einer Bremse blockieren) ist es unmöglich die Last
ohne den Motor anzuheben. Es liegt daher nahe eine neue
Grösse einzuführen, in der neben der Kraft auch die
"erbrachte" Höhe mit eingeht.
FZ
m
FG
Definition:
Physikalische Arbeit wird (nur dann) verrichtet, wenn ein Körper mit Kraftaufwand über eine Strecke s
bewegt wird:
W = FS · s
Arbeit (Work) = Kraft mal Weg
Beachte: FS ist dabei die Kraft in Wegrichtung!
(s. unten)
Einheit: 1 N · 1 m = 1 Joule
Zahlenbeispiel: 4 kg halten: W = FG· s = FG· 0 m = 0 !
4 kg um 2 m anheben: W = FG·s = 4 kg· 9.81 m/s2· 2 m = 78.48 N·m ≈ 78.5 J
Für die Arbeit ist von allen Kräften nur die massgebend, welche auch in Richtung des vorgegebenen Weges
zeigt. Als Beispiel betrachten wir das Ziehen eines Schlittens an einem Seil:
FZug
FS
S
Zur Berechnung der Arbeit darf nicht direkt die Zugkraft FZ verwendet werden, sondern man muss die
Projektion von FZ auf die Strecke s verwenden: FS = FZ · cosα
Also ist in diesem Fall:
W = FZ · cosα· s
21
3.2 Die Leistung
Wird ein Gewicht wie bei dem Kran nach oben gezogen, spielt für den Motor neben der Arbeit auch noch die
Zeit eine Rolle, in der die Arbeit erbracht wird. Je kürzer diese ist, desto schneller muss der Motor die Arbeit
liefern, man sagt er muss mehr Leistung besitzen. (Dieses Mal stimmt der Begriff auch mit unserer
Alltagssprache überein, auch hier wird eine Leistung um so höher "bewertet" , je schneller sie erbracht wird.)
Man definiert daher Leistung als Arbeit pro Zeit:
Einheit: 1 Joule/ Sekunde = 1 Watt [1 W]
P = W/t
(Nach James Watt, Erfinder der Dampfmaschine)
Vorsicht: W als Einheit nicht mit dem W für die Arbeit verwechseln!
1 Watt ist eher eine kleine Einheit, daher werden im Alltag Leistungen häufig auch in Kilowatt [kW] oder im
Zusammenhang mit der Energiewirtschaft in Megawatt [MW] angegeben, wie folgende Beispiele zeigen:
Leistung
MP 3 – Player, Geräte im Standby, Sparlampen
bis 10 W
Mensch (Grundbedarf), Laptop, Glühlampen, Kühlschrank
50 - 100 W
Hochleistungssportler, Haarföhn, Waschmaschine
1 - 3 kW
Sonneneinstrahlung bei klarer Atmosphäre pro m2 Fläche
1300 W
mittlerer Verbrauch einer in der Schweiz lebenden Person
5 kW
PKW
50 – 200 kW
ICN
10 MW
Grosskraftwerk (z.B. Gösgen)
Sonne absolut
2 000 MW
3.83 · 1026 W
Eine veraltete Einheit der Leistung ist die Pferdestärke: 1 PS ≈ 736 Watt. Diese Einheit stammt noch aus der
Zeit der industriellen Revolution, als Pferde dazu eingesetzt wurden, Wasser aus Bergwerkschächten zu
"pumpen", indem sie immer im Kreis laufend ein Schöpfrad antrieben. Die Fördermenge war dann ein Mass
für die Leistung des Pferdes, aus Sicht des Tierschutzes also eine ziemlich unschöne Definition!
3.2.1 Die Kilowattstunde
Für den Anfänger ist etwas verwirrend, dass man in der Technik die Einheit der Arbeit (und damit der
Energie, wie wir später sehen werden) manchmal wieder auf die Leistung zurückführt. Stellt man die
Definition um ist: W = P · t
Für P = 1 Watt und t = 1 s erhält man daraus sofort 1 J = 1 Ws (Wattsekunde)
Im Alltag kann man mit einer Leistung von 1 W innerhalb 1 Sekunde aber nicht viel anfangen. Daher
verrechnet man (insbesondere bei der Stromrechnung) häufig 1 kW mit 1 Stunde und nennt diese Einheit
Kilowattstunde: 1 kW · 1 h = 1000 W·3600 s = 3 600 000 J
Merke: Die Kilowattstunde ist eine Einheit für die Arbeit und entspricht genau 3.6 MJ.
Wenn man sich also z. B. mit einem Föhn mit 1500 W Leistung 10 Minuten lang die Haare föhnt, liefert das
Elektrizitätswerk eine Arbeit von W = 1.5 kW· 10/60 h = 0.25 kWh
Nachdem wir nun die Grundbegriffe kennen gelernt haben, soll im nächsten Kapitel untersucht werden, wie
bei verschiedenen Vorgängen Arbeit und Leistung bestimmt werden kann.
22
3.3 Verschiedene Formen von Arbeit
Je nachdem, durch welche Kraft die Arbeit verrichtet wird, unterscheidet man verschieden Formen der
Arbeit. In der Mechanik sind folgende Varianten von Bedeutung:
3.3.1 Hubarbeit
Die Hubarbeit haben wir schon im vorigen Kapitel kennengelernt, sie wird verrichtet, wenn ein Körper der
Masse m (gegen die Gewichtskraft) um die Höhe h angehoben wird:
WHub = FG ·s = m·g·h
Dabei muss der Weg aber nicht immer "direkt" nach oben
führen :
Betrachtet man einen Körper der eine schiefe Ebene
hochgeschoben wird, wird dieser indirekt angehoben. Wir
bestimmen zunächst die Kraft FS, die dazu notwendig ist.
Nach nebenstehender Abbildung wirken auf den Wagen
zunächst die Gewichtskraft FG und die Normalkraft FN. Die
Resultierende diese beiden Kräfte würde den Wagen nach
unten beschleunigen und wird Hangabtriebskraft FHg
genannt. Genau mit der gleichen Kraft muss der Wagen
aber auch nach oben gestossen werden, daher gilt:
FS = FHg = FG · sin α = m· g· sin α
sin α = FHg / FG
FN
(-) FHg
s
FG
α
h
α
Damit berechnen wir die Arbeit:
W = FS· s = m· g· sinα· s
Andererseits ist aber sinα = h/s , woraus sich sofort wieder
WHub = m·g·h ergibt!
Im Ergebnis kommt es nur auf die gewonnene Höhe an, die Hubarbeit ist unabhängig davon, welchen
Weg man dabei einschlägt!
Beispiel: Wasserkraftwerk
Die (mittlere) Höhendifferenz (Staumauer Kraftwerk) betrage 500 m, der Stausee sei bei
einer Fläche von drei Quadratkilometerm 40 m
tief. Wir berechnen die Arbeit, welche durch das
Wasser (gesamt) verrichtet werden kann und die
Leistung, wenn pro Stunde 100 000 m3 Wasser die
Turbine durchströmen kann:
Stausee
h1
Zunächst ist VGes = A·h1 = 1.2·108 m3
h2
und die Masse des Wassers:
m = ρ· V = 1.2 · 1011 kg
(ρW = 1000 kg/m3 !)
Turbine
Damit erhält man WGes = m· g· h2 ≈ 5.89 · 1014 J
Für die Leistung der Turbine verwenden wir
m' = 1·108 kg
und t = 3600 s:
⇒ W' = m'· g· h2 ≈ 4.91· 1011 J
und P = W' /t ≈ 1.36·108 W = 136 MW
Damit lässt sich eine Stadt in der Grösse von Solothurn mit elektrischer Energie versorgen, und zwar
für t = Wges/P ≈ 4328 000 s ≈ 50 d .
23
3.3.2 Beschleunigungsarbeit
Auch bei der Beschleunigung eines Fahrzeugs wirkt eine
Kraft entlang des Weges, also wird Arbeit verrichtet. Wir
gehen von einer gleichmässig beschleunigten Bewegung aus,
die entsprechende Kraft beträgt: F = m·a
und die
Beschleunigungsarbeit ist WB = m·a·s
Verwendet man für die zurückgelegte Strecke s =
oder:
v2
2⋅a
F
s
erhält man WB = m·a·
v2
2⋅a
W B = ½ · m · v2
Zahlenbeispiel: m = 1200 kg;
v = 90 km/h = 25 m/s
WB = ½ · 1200 kg· (25 m/s)2 = 600 kg· 625 m2 /s2 = 375 000 J = 375 kJ
3.3.3 Spannarbeit einer Feder
Dehnt oder staucht man eine Feder, muss ebenfalls Arbeit verrichtet werden, diese nennt man die
Spannarbeit. Um sie zu bestimmen muss man erst die Kraft kennen, die zum Spannen der Feder notwendig
ist. Nach dem Hook'schen Gesetz ist sie proportional zur Ausdehnung s der Feder: F ≈ s
Dies bedeutet, dass der Quotient
D = F/s
konstant ist. D heisst Federkonstante.
Berechnung der Arbeit:
Ist s die Strecke, um die die Feder gedehnt wird, gilt
im Prinzip wieder W = F ·s.
Aber:
Während des Dehnens ändert sich die Kraft. Zu
Beginn ist sie praktisch null, nachdem die Feder
um s gedehnt wurde, beträgt sie Fmax = D·s.
Die Arbeit bezieht sich aber auf den "Prozess" der
Dehnung, d. h man muss mit der mittleren Kraft
rechnen. In unserem Fall ist dies gerade die Hälfte
von Fmax, also F = ½ D·s
F
s
F
F
Fmax
Damit erhält man:
WS = ½ D·s2
FMittel
Spannarbeit einer Feder
Zahlenbeispiel: Eine Feder wird durch 30 N um 20 cm gedehnt.
s
Die Federkonstante beträgt D = F/s = 30 N/ 0.2 m = 150 N/m
und die verrichtete Arbeit: W = ½ D s2 = ½ ·150N/m· (0.2 m)2 = 3 Joule
3.3.4 Die Reibungsarbeit
Wird ein Körper gegen die Reibungskraft bewegt, muss gleichfalls Arbeit verrichtet werden: W = FR· s
Die Reibungskraft war: FR = µ ·FN = µ ·m· g· cosα
Damit ist die verrichtete Arbeit:
(µ : Reibungskoeffizient, FN: Normalkraft)
WR = µ · m · g· cosα · s
24
3. 4 Die Energie
Ein Stein wird vom Boden auf eine Mauer gehoben und dort abgelegt. Nach dem
vorigen Kapitel wird an ihm Hubarbeit verrichtet. Auch wenn anschliessend der
Stein auf der Mauer liegt, muss diese Arbeit immer noch vorhanden sein: sobald
der Stein herunterfällt kann er jemanden erschlagen. Die Arbeit war
gewissermassen gespeichert.
Gespeicherte Arbeit nennt man Energie.
Energie hat die Fähigkeit, Arbeit zu verrichten
Obwohl beides eng miteinander verwandt ist, sind Arbeit und Energie nicht das
Gleiche. Das Verrichten einer Arbeit kann man sich als aktiven Prozess
vorstellen, während die Energie einen passiven Zustand beschreibt.
Um Energien zu bestimmen, kann man aber die entsprechende Arbeit berechnen und auch die Einheit bleibt
das Joule. D. h. rein mathematisch kann man Energie und Arbeit gleich behandeln. Nach dem vorigen
Kapitel erhält man daher die:
Lageenergie oder potentieller Energie:
ELage = m· g· h
Bewegungsenergie oder kinetische Energie : Ekin = ½ m· v2
Spannenergie:
ESpann = ½ D·s2
Bei der Reibung macht es dagegen keinen Sinn von "Reibungsenergie" zu sprechen, da sie in unserem Sinne
nicht gespeichert wird. In der Wärmelehre werden wir sehen, dass Reibungsarbeit in die sogenannte innere
Energie umgewandelt wird,
Eine Besonderheit ist bei der potentiellen Energie (Lageenergie)
zu beachten. Diese kann immer nur auf ein bestimmtes Niveau
(auch Nullniveau genannt) bezogen werden. Dies kann, muss
aber nicht, der Erdboden sein. Denn selbst ein Körper, welcher
auf dem Boden liegt, kann noch Lageenergie besitzen, z. B. kann
man ihn immer noch in einen Brunnen werfen!
E1
E2
Das Nullniveau kann man im Prinzip frei wählen,
geschickterweise sucht man meistens den tiefsten Punkt, der für
eine gegebene Problemstellung in Frage kommt (Beispiele
später). Befindet sich ein Körper trotzdem einmal unter dem
Nullniveau, muss man seine potentielle Energie negativ rechnen.
Bei der Bestimmung der potentiellen Energie eines Körpers bezieht man sich auf ein vorher
bestimmtes Nullniveau. Dieses kann beliebig gewählt werden, vorteilhaft nimmt man den
tiefsten Punkt, den ein Körper in der betrachteten Situation erreichen kann (um negative Werte
zu vermeiden).
Es sollte klar sein, dass man zwei oder mehr potentielle Energien nur dann sinnvoll miteinander vergleichen
kann, wenn sie sich auf dasselbe Nullniveau beziehen!
25
3. 5 Energieerhaltung
Die physikalische Bedeutung der Energie wird erst klar, wenn man verschiedene Formen miteinander
vergleicht. Dazu machen wir folgendes Experiment:
Eine an einer Schnur befestigte Masse
schwingt als Pendel durch eine Lichtschranke. Wir messen die "Starthöhe" h und
über die Dunkelzeit (vgl. Kap. 1.4.) die
Geschwindigkeit der Kugel im tiefsten
Punkt. Aus diesen Werten können wir
Lage- und kinetische Energie in den beiden
verschiedenen Positionen berechnen und
miteinander vergleichen:
Es ist m = 0.3 kg
h
h [m]
00.14
v
EL = m·g·h [J]
0.05
0.1
0.147 0.294
0.15
0.44
v [m/s]
1
1.4
1.7
Ekin = ½ m·v2 [J]
0.15
0.294
0.43
Ergebnis: Die Lageenergie wird praktisch vollständig in kinetische Energie verwandelt !
Die Umwandlung von Energie lässt sich auch bei vielen anderen Vorgängen beobachten und führt uns zu
einen der grundlegendsten Aussagen in der Physik. Bezieht man alle an dem Vorgang beteiligten
"Komponenten" mit ein (im weiteren Sinne z. B. auch die Bewegung der Moleküle und damit die innere
Energie) und betrachtet dies als ein sogenanntes abgeschlossenes System, stellt man fest:
In einem abgeschlossenem System bleibt die Gesamtenergie konstant. Die einzelnen Energieformen
können sich dabei ineinander umformen. Im Falle der Reibung entsteht Wärme bzw. innere Energie.
Weiteres Beispiel: "Bungee - Jumping"
Ein Massestück fällt an einem Gummiseil (vergleichbar mit einer Feder) zu Boden. Wir suchen die maximal
mögliche Ausgangshöhe, so dass der "Springer" gerade den Boden "touchiert".
bekannt sind: m = 1 kg , D = 35 N/m , s = 1.1 m
(s ist die Strecke, um welche das Seil im tiefsten Punkt gedehnt wird
und im allgemeinen kleiner als h, da das Seil ja nicht von Beginn an
unter Spannung ist!)
gesucht: h
Idee: Die Lageenergie des "Springers" wird vom Seil aufgenommen:
h
"Start": E1 = m·g·h
s
tiefster Punkt: E2 = ½ D· s2
gleichsetzen: m·g·h = ½ D· s2
⇒
h=
D ⋅ s2
≈ 2.16 m
2⋅m⋅g
Zusatzaufgabe: Bestimme die Geschwindigkeit des Springers bei der halben Fallhöhe!
26
3. 6 Der Wirkungsgrad
In der Realität bleibt die Energie eines mechanischen Systems (leider) in den seltensten Fällen vollständig
erhalten, sondern wird mehr oder weniger schnell durch Reibung oder Luftwiderstand "verbraucht", d. h. als
Wärme an die Umgebung abgegeben. Um diesen Prozess mit einzubeziehen, gibt es grundsätlich zwei
Möglichkeiten:
•
Man kann das ganze System erweitern und versuchen, die Umgebung mit der darin enthaltenen inneren
Energie einzuberechnen.
•
Man nimmt die Wärmeverluste in Kauf und geht davon aus, dass die Energie des betrachten Systems
kleiner wird.
Die erste Methode setzt tiefere Kenntnisse aus der Wärmelehre voraus, ist aufwendig und hat für den Alltag
fast keine Bedeutung. Daher betrachten wir die 2. Methode, die auch in der Technik häufig angewandt wird
und uns auf den Begriff des Wirkungsgrad führt.
Man geht davon aus, das für einen
Vorgang eine bestimmte Menge Energie
(in Form von Treibstoff, Lageenergie,
EVerlust
auch Wärmeenergie) zur Verfügung
steht, häufig als Gesamtenergie EGes oder
Eges
Prozess
als zugeführte Energie EZu bezeichnet.
W Nutz
Ein Teil dieser Energie kann bei einem
Prozess nach unseren Massstäben
sinnvoll genutzt werden, in dem
mechanische Arbeit WNutz verrichtet
wird. Der andere Teil wird als Verlustenerige EVerlust bezeichnet. Man erkennt sofort, dass
EGes = WNutz + EVerlust
Unter dem Wirkungsgrad versteht man nun das Verhältnis der verrichteten Arbeit zur gesamten Energie:
η = WNutz/ Eges
Bemerkung: Ob man in diesem Zusammenhang besser von Arbeit oder von Energie spricht, ist nicht ganz
einheitlich, man findet beide Versionen. Die gleichen Beziehungen gelten natürlich auch, wenn man die
Leistung betrachtet. Daher gilt auch:
η = PNutz /PGes
Der Wirkungsgrad ist eine dimensionslose Zahl zwischen 0 und 1, wird aber manchmal als Prozentzahl
angegeben.
Beispiel: η = 0,42 = 42 % bedeutet, dass 42% der verfügbaren Energie tatsächlich gebraucht werden
können. Die eigentliche Bedeutung des Wirkungsgrades werden wir erst in der Wärmelehre kennen lernen,
wenn wir "Wärmeverluste" ebenfalls berechnen können.
In einem Versuch bestimmen wir den Wirkungsgrad eines Elektromotors, welcher ein Gewichtstück nach
oben zieht. Die aufgenommene Energie kann ein Messgerät über die Spannung und den Strom messen:
Eges = 33.4 J
Wir nutzen den Motor für Hubarbeit, daher gilt Wnutz = 1 kg · 9.81 m/s2 · 2m = 19.26 J
Damit ist η = 19.26 J / 33.4 J ≈ 0.577 = 57.7 %
und WVerlust = Eges – Wnutz = 14.14 J
27
Ergänzung: Arbeit bei beliebigen Kraftgesetzen
"Professionelle" Bogenschützen verwenden heutzutage Verbundbögen, die
die Eigenschaft besitzen, dass die
Kraft ab einer gewissen Spannung des
Bogens wieder abnimmt. Dadurch
erreicht man, dass der Arm entlastet
wird und man sich besser und länger
auf das Zielen konzentrieren kann. Das
nebenstehende Diagramm zeigt in etwa
den Verlauf der Kraft eines solchen
Bogens.
Natürlich wird beim Spannen des
Bogens auch Arbeit verrichtet. Diese
soll nun direkt aus dem Diagramm
bestimmet werden.
180
Dazu teilt man sich in Gedanken den
Spannprozess in kleine Schritte (im
Beispiel zu 0.05 m) auf.
Für jeden dieser Schritte berechnet
man nach W = F · s die Arbeit, wobei
für die Kraft der Wert bei der "Mitte"
des jeweiligen Schrittes verwendet
wird. Im Beispiel wäre also in etwa
180
W = 16 N· 0.05 m + 45 N· 0.05 m +
73 N· 0.05 m + 105 N· 0.05 m + ...
100
40
Kennt man die Funktionsgleichung der
Kurve, kann man diese Fläche im
allgemeinen auch berechnen (Integralrechnung), leider (oder glücklicherweise, je nach Standpunkt), wird dies
in der Mathematik aber erst im letzten
Jahr behandelt.
0,2
0,4
0,6
0,2
0,4
0,6
0,2
0,4
0,6
s [m]
F [N]
100
40
Das erscheint zunächst mühsam und
zudem kann man kritisieren, dass die
für die Kraft verwendeten Werte auch
nur ungefähr richtig sind.
Der nächste Schritt macht aber den
Sinn dieser Überlegungen klar: Macht
man die Unterteilung immer feiner,
erkennt man, dass man eigentlich "nur"
die Fläche unter der Kurve
bestimmen muss. Diese entspricht der
verrichteten Arbeit.
F [N]
0,05
180
s [m]
F [N]
100
40
s [m]
Wir können uns jedoch damit behelfen, dass wir die Fläche durch Auszählen der Häuschen bestimmen, im
Beispiel entspricht jedes Häuschen einer Arbeit von 10 N · 0.025 m = 0.25 J ! Durch die "Grenzfälle" direkt
bei der Kurve hat man zwar immer noch eine Fehlerquelle, man erhält dennoch ein recht gute Abschätzung
für die Arbeit.
28
Aufgaben
1) Bestimme die Arbeit für den beschriebenen Pfeilbogen.
2) Bestimme so genau wie möglich die Arbeit bei den folgenden Diagrammen.
F [N]
F [N]
8
10
5
6
2
2
0,2
0,5
1
0,1
s [m]
F [N]
F [N]
10
50
0,5
s [m]
6
10
2
0,1
0,5
s [m]
1
5
3) Begründe mit dem Kraft-Weg-Diagramm, dass bei einer "normalen" Feder die Spannenergie
s [m]
D⋅s2
2
beträgt!
29
Zusammenfassung Arbeit und Energie:
Wird längs eines Weges eine Kraft ausgeübt wird dabei Arbeit verrichtet: W = Fs ·s
In der Mechanik unterscheidet man folgende Formen der Arbeit:
Hubarbeit:
WH = m ·g ·h
Beschleunigungsarbeit:
WB = 1/2 m· v2
Spannarbeit (Feder):
WS = 1/2 D· s2
Reibungsarbeit:
WR = µ· FR·s
Arbeit pro Zeit nennt man Leistung: P = W/t
Gespeicherte Arbeit nennt man Energie (Ausnahme: Reibung). Die verschiedenen Energieformen können sich
ineinander umformen, die Gesamtenergie bleibt dabei jedoch gleich; dies hilft uns beim Lösen von Aufgaben!
Schliesslich versteht man unter dem Wirkungsgrad das Verhältnis von nutbarer Energie zur Gesamtenergie;
η = WNutz/ Wges
30