Das elektrische Feld eines geladenen Metallkörpers

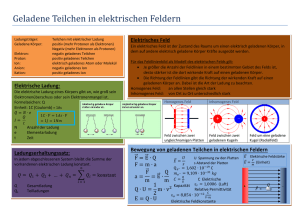
Das elektrische Feld eines geladenen Metallkörpers
1. Im Metall sind Ladungen frei beweglich.
2. Potentialdifferenzen zwischen zwei Punkten einer Metallfläche
werden sofort abgebaut.
3. Daraus ergeben sich folgende Aussagen:
• Es existiert kein elektrisches Feld tangential zur Metallfläche,
d.h.
r
r
Et = Dt = 0
r
r
r
D N = σ frei = ε 0 E N − MO = ε 0 ε r 2 E N 2
• Jede leitende Fläche ist Äquipotentialfläche
• Die Flächenladungsdichte einer geladenen Metallfläche ist
konstant und erzeugt ein Feld senkrecht zur Fläche.
Für das Feld an der Oberfläche gilt:
r
σ
E N = frei
ε0
Der Faradaykäfig
• Ein Faradaykäfig ist eine zusammenhängende, hohle
Metallfläche.
• Die Innenfläche ist Äquipotentialfläche, d.h. V = const. ⇒
r
r
V ( ri ) − V ( rj ) = 0
für jeden Ort r der Metallfläche.
• Die Feldstärke im Inneren des Käfigs ist Null. Dies folgt sofort
aus dem Gauß’schen Satz, da die Ladung im Inneren des
Hohlraumes Null ist. ⇒
Die Relation V = const. gilt für den gesamten Hohlraum und
nicht nur für die Innenfläche.
• Die gesamte Oberflächenladung sammelt sich auf der
Außenfläche und erzeugt ein E-Feld senkrecht zur Oberfläche.
Das elektrische Feld einer geladenen Metallfläche
r
E
+
+
+
r
−E
+
r
E
+
+
r
dA
+
r
−E
r
− dA
σ
+
Mit Hilfe des Gauss’schen Satzes findet man
r r Q
E
∫ dA = e
findet man
( )( )
r
r r r r
r
Q
E
d
A
=
E
⋅
A
+
−
E
⋅
−
A
=
= 2EA
∫
e
Da sich die Normalkomponente des elektrischen Feldes aus der
Oberflächenladungsdichte E = σ/ε0 ergibt, folgt:
E=
σ
2ε 0